Абсолютная и относительная погрешность — методы и алгоритмы вычислений

Введение

Все, что сказано в этом введении, запоминать не нужно. это справочный материал, к которому вы будете обращаться при выполнении лабораторных работ.

1. Как определять погрешности измерений

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

A, B, C, … — физические величины.

A_пр — приближенное значение физической величины, т.е. значение, полученное путем прямых или косвенных измерений.

ΔA — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

Δ_иA — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; указывается в каждой работе при описании прибора в разделе Оборудование и средства измерения)

Δ_оA — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения), она равна в большинстве случаев половине цены деления; при измерении времени — цене деления секундомера или часов.

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

ΔA=Δ_иA + Δ_оA

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔA≈0,17=0,2); численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А=10,332≈10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, отличаются друг от друга.

В этом случае A_пр находят как среднее арифметическое значение всех измерений, а ΔA (ее в этом случае называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. При этом для получения результата достаточно одного измерения.

Относительная погрешность косвенных измерений определяется, как показано в таблице 1.

Абсолютная погрешность косвенных измерений определяется по формуле ΔA=A_прε (ε выражается десятичной дробью).

Таблица 1

Формулы для нахождения относительной погрешности косвенных измерений

Nº п/п	Формула физической величины	Формула относительной погрешности
1
2
3	A=B+C
4

2. О классе точности электроизмерительных приборов

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ_пр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность Δ_иA от всей шкалы прибора (A_max):

Класс точности указывается при описании прибора в разделе Оборудование и средства измерения. Cуществуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ_пр) и всю его шкалу (A_max), определяют абсолютную погрешность Δ_иA измерения физической величины А этим прибором:

3. Как сравнивать результаты измерений

1. Записать результаты измерений в виде двойных неравенств:

A_{1 пр} – ΔA₁ < A_{1 пр} < A_{1 пр} + ΔA₁A_{2 пр} – ΔA₂ < A_{2 пр} < A_{2 пр} + ΔA₂
2. Сравнить полученные интервалы значений (рис.1): если интервалы не перекрываются, то результаты неодинаковы, если перекрываются — одинаковы при данной относительной погрешности измерений.

Рисунок 1.

4. Как оформлять отчет о проделанной работе

Отчетом о проделанной работе является форма, находящаяся в левом нижнем окне. После ее заполнения надо нажать на кнопку «Отправить результаты на сервер».

Значения измеренных физических величин переносятся в таблицу результатов автоматически после нажатия соответствующей кнопки.

Значения остальных величин и ответ на контрольный вопрос вводятся с клавиатуры.

домашней странице BARSIC

Как найти погрешность: эксперимент с линейкой

Обнаружить явление погрешности можно самостоятельно вне строгой лабораторной обстановки: достаточно провести простой эксперимент измерения длины с обычной школьной линейкой. В качестве примера, возьмем карандаш и выполним с ним замеры.

Рисунок 2. Замер линейкой с ценой деления 1 см.

Во-первых, необходимо зафиксировать цену деления измерительного прибора. Цена деления определяется разностью двух ближайших отметок. В нашем случае она равна 1 см.

Примечание. На разметке измерительного прибора всегда указываются единицы измерения. К примеру, на стандартной линейке можно увидеть пометку «см», сантиметры.

Довольно часто используемые для измерений приборы не работают с основными единицами СИ — единицы величин либо являются производными, как сантиметр, либо, как миллиметр ртутного столба, являются внесистемными.

{"questions":,"answer":}}}]}

Когда вас просят привести ответ в СИ, не забывайте о переводе значений, если измерительный прибор работает с внесистемными или производными единицами. В случае с сантиметровой линейкой, при подобном требовании, обязательно выражение результата в метрах и т. п.  

Далее совмещаем конец карандаша с нулевой отметкой. Видим, что второй конец располагается между отметками 12 и 13.

Какой из этих результатов следует принять за длину нашего карандаша?

Очевидно, что тот, который будет ближе к истинному значению — 12 см. Если бы мы провели аналогичный опыт, использовав более точную линейку с ценой деления в миллиметр, мы получили бы значение 12.2 см.

Рисунок 3. Замер линейкой с ценой деления 1 мм

А какой из этих результатов лучше будет засчитать теперь? Какой правильный?

Оба результата фактически являются верными, их разница заключается лишь в том, что получены они были с разной точностью измерения: длина карандаша во втором варианте была дана с точностью до миллиметра, в первом — до сантиметра. Можно было бы воспользоваться микро́метром, еще более точным измерительными прибором, и получить результат с точностью до микроме́тра. Однако в случае с карандашом точности до миллиметра будет достаточно.

Наш ответ: 12.2 см.

Методы Корнфельда и Стьюдента

Некоторые экспериментальные исследования требуют многократного измерения одного и того же показателя с помощью аппаратуры или приспособлений. В этом случае высока вероятность возникновения отклонений разброса. Определить ее величины можно разными способами. Самый распространенный и доступный из них называется по автору — методом Корнфельда.

Он применяется в ситуации, когда какая-либо физическая величина была измерена n раз. В этом случае рекомендован следующий порядок действий:

1. Предполагается, что имеется ряд результатов измерений от Х1 до Хn.
2. Из этих величин выбирают минимальную и максимальную.
3. Вычисляют среднее значение Х.
4. В пределах от наименьшего до наибольшего показателя выбирают доверительный интервал.
5. Чтобы найти абсолютное отклонение, необходимо вычесть из максимального результата измерения величину минимального. Полученную разность делят пополам.

Метод Корнфельда имеет существенный недостаток. Чтобы определить вероятность приведенного результата, необходимо провести большое количество измерений. При этом нет возможности изменить границы доверительного интервала. Более точные данные можно получить, используя метод расчета Стьюдента. Для этого используют специальные таблицы, где отражены так называемые коэффициенты Стьюдента.

Что такое точность измерений?

Точность измерений характеризует близость результата измерения к фактическому значению измеряемой величины. Строго говоря, ни одна физическая величина не может быть измерена с абсолютной точностью. То есть так, чтобы данные измерительного прибора отображали истинное значение.

Мир и его явления, на самом деле, практически всегда имеют отношение к иррациональным числам. Таким, как, к примеру, результат деления десяти на три. Наберите, кстати, данную операцию на калькуляторе и посмотрите на то, как неэстетично в реальности выглядят данные — с кучей знаков после запятой, за которыми не угнаться.

{"questions":[{"content":"Откройте ниже встроенный калькулятор и поделите $25$ на $7$. Сколько знаков после запятой выводит калькулятор в результате вычислений? Введите ниже <b>количество знаков после запятой</b>. `input-1`","widgets":{"input-1":{"type":"input","answer":"6"}},"step":1,"calc":1,"hints":},{"content":"А теперь возьмите полученное вами число ($3.571429$) и умножьте его «обратно» на семь. Каким вышел результат? `choice-6`","widgets":{"choice-6":{"type":"choice","options":,"explanations":,"answer":}},"calc":1}],"mix":1}

Однако иррациональность чисел не удивляет, да и слишком абстрактна, дабы уловить суть. Что есть деление? Тогда, для конкретности, стоит покуситься на святое — на время. Казалось бы, что может быть точнее времени, показываемого самыми точными на свете часами — атомными часами?

И тем не менее, даже если вы зайдете на онлайн-ресурс, официально регистрирующий международное атомное время с точностью до миллисекунд, действительного точного измерения времени там вы не найдете.

Всегда есть условности: задержка передачи данных между сетевыми элементами; ваш мозг, регистрирующий и обрабатывающий информацию, поступающую через органы чувств и т. д. Все это отдаляет нас, хоть и несущественно, от фактического значения величины времени.

Именно поэтому в физике одним из важнейших понятий является понятие погрешность измерений.

Абсолютная и относительная погрешность

Абсолютной погрешностью или, короче, погрешностью приближенного
числа называется разность между этим числом и его точным значением (из большего числа вычитается меньшее)*.

Пример 1. На предприятии 1284 рабочих и служащих. При
округлении этого числа до 1300 абсолютная погрешность
составляет 1300 — 1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 — 1280 = 4.

Относительной погрешностью приближенного числа называется отношение
абсолютной погрешности приближенного числа к самому этому числу.

Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная
погрешность составляет 200 — 197 = 3. Относительная погрешность равна 3/197 или, округленно, 3/197 = 1,5 %.

В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности.
Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.

Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза
неизвестен. Но абсолютная погрешность не
превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈ 1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью. Число, заведомо превышающее
относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.

В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность — 1,4 %.

Величина предельной погрешности не является вполне определенной. Так, в примере 3 можно принять за предельную абсолютную
погрешность 100 г, 150 г и вообще всякое число, большее чем 50 г. На практике берется по возможности меньшее значение
предельной погрешности. В тех случаях, когда известна точная величина погрешности, эта величина служит одновременно
предельной погрешностью. Для каждого приближенного числа должна быть известна его предельная погрешность
(абсолютная или oотносительная). Когда она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания
предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого
соглашения всегда можно обойтись без указания предельной погрешности числа.

Предельная абсолютная погрешность обозначается греческой буквой Δ («дельта»); предельная относительная
погрешность — греческой буквой δ («дельта малая»). Если приближенное число обозначить буквой а, то

δ = Δ/a.

Пример 4. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная
относительная погрешность этого измерения?
Здесь а = 17,9 см; можно принять Δ = 0,1 см, так как с точностью до 1 мм измерить карандаш нетрудно, a значительно уменьшить, предельную погрешность ни удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого карандаша ребра могут разниться на бoльшую величину). Относительная погрешность равна 0,1/17,9.
Округляя, находим δ = 0,1/18 ≈ 0,6%.

Пример 5. Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы
предельная относительная погрешность составляла 0,05%?Решение. По условию, предельная абсолютная погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная
абсолютная погрешность равна 36*(0,05/100) = 0,0175 (мм) или, усиливая, 0,02 (мм). Можно воспользоваться
формулой δ = Δ/a.
Подставляя в неё а = 35, δ = 0,0005, имеем 0,0005 = Δ/35. Значит, Δ = 35 • 0,0005 = 0,0175 (мм).

* Иначе говоря, если a есть приближенное число, а х – его точное значение, то абсолютная погрешность есть абсолютное
значение разности a – х. В некоторых руководствах абсолютной погрешностью называется сама
разность a – х (или разность х — a). Эта величина может быть положительной или отрицательной.

Абсолютная погрешность — измерительный прибор

Абсолютная погрешность измерительного прибора представляет собой расхождение ( разность) между измеренным Ли и действительным ( истинным) Лд значениями измеряемой величины ДЛ — / 4н — Ац. Истинное значение измеряемой величины находят с учетом поправки. Поправка — это величина, обратная по знаку абсолютной погрешности: ДР — ДЛ Ал-А. Абсолютная погрешность электроизмерительных приборов со стрелочным показателем практически неизменна в пределах всей шкалы, поэтому с уменьшением значения измеряемой величины она возрастает. Для повышения точности измерения измеряемой величины на показывающих приборах со стрелочным указателем следует выбирать такие пределы измерения, чтобы отсчитывать показания примерно в пределах 2 / 3 всей шкалы.
 

Абсолютная погрешность измерительного прибора равна разности между показанием прибора и действительным ( точным) значением измеряемой величины.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и истинным значением измеряемой величины. Погрешность показаний прибора имеет своими источниками погрешности отдельных его элементов: чувствительного элемента, передаточного механизма и шкалы. Погрешность чувствительного элемента заключается в том, что действительная зависимость его перемещений от измеряемой величины не совпадает с расчетной, заложенной в схему прибора. Погрешность шкалы складывается из ошибки положения ее штрихов и эксцентриситета шкалы.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Так как истинное значение измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Поскольку последнее установить нельзя, то в измерительной технике используют так называемое действительное значение, полученное посредством образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины Так как величину истинного значения измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Приведенная погрешность измерительного прибора — отношение абсолютной погрешности измерительного прибора к нормирующему значению, выраженное в процентах.
 

Корректность поставленных экспериментов доказана отсутствием превышения абсолютных ошибок измерения как при определении перемещений, так и напряжений над абсолютной погрешностью используемых измерительных приборов.
 

В некоторых случаях ( для образцовых и рабочих средств измерений повышенной точности) для исключения систематической погрешности показаний вводят поправку, равную абсолютной погрешности измерительного прибора.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и действительным значением измеряемой величины.
 

В данном разделе будут рассмотрены виды погрешностей, свойственные мерам, отдельным элементам и устройствам, а также средствам измерений в целом. Под абсолютной погрешностью меры понимают разность ( отклонение от номинального значения) между номинальным значением меры и истинным значением воспроизводимой ею величины. Так как истинное значение величины остается неизвестным, то на практике вместо него используют действительное значение величины. Следует различать абсолютную погрешность измерительного преобразователя по входу и по выходу. Абсолютную погрешность измерительного преобразователя по входу находят как разность между значением величины на входе преобразователя, определяемой в принципе по истинному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и истинным значением величины на входе преобразователя. Абсолютную погрешность измерительного преобразователя по выходу находят как разность между истинным значением величины на выходе преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемой в принципе по истинному значению величины на выходе с помощью градуировочной характеристики, приписанной преобразователю. Относительная погрешность измерительного прибора определяется как отношение абсолютной погрешности измерительного прибора к истинному значению измеряемой им величины.
 

Расчёт ошибок косвенных измерений

Пусть искомая
величина Апри выбранном
методе косвенных измерений рассчитывается
по формуле:

A
= f(x₁
,x₂
,x₃
,…,x_n
) (12)

где x₁,x₂,…,x_n
— величины, найденные в результате прямых
измерений, с учётом ошибок о которых
шла речь выше. Из-за этих ошибок величина
«А»
так же будет определяться с ошибками.

Пусть X₁,X₂,…,X_N
— значения f(x₁
,x₂
,x₃
,…,x_n), вычисленные
для разных серий измерений (x₁,x₂,…,x_n).

Таблица 1

Таблица коэффициентов
Стьюдента

Число измерений	Доверительная вероятность
0.7	0.8	0.9	0.95	0.99	0.999
2	2.0	3.1	6.3	12.7	63.7	636.6
3	1.3	1.9	2.9	4.3	9.9	31.6
4	1.3	1.6	2.4	3.2	5.8	12.9
5	1.2	1.5	2.1	2.8	4.6	8.6
10	1.1	1.4	1.8	2.3	3.3	4.8
15	1.1	1.3	1.8	2.1	3.0	4.1
20	1.1	1.3	1.7	2.1	2.9	3.9

Абсолютной ошибкой
косвенных измерений, по аналогии с
аб­солютной ошибкой прямых измерений,
называют разность между ис­тинным
значением «А» и её значениями,
полученными в результате измерений:

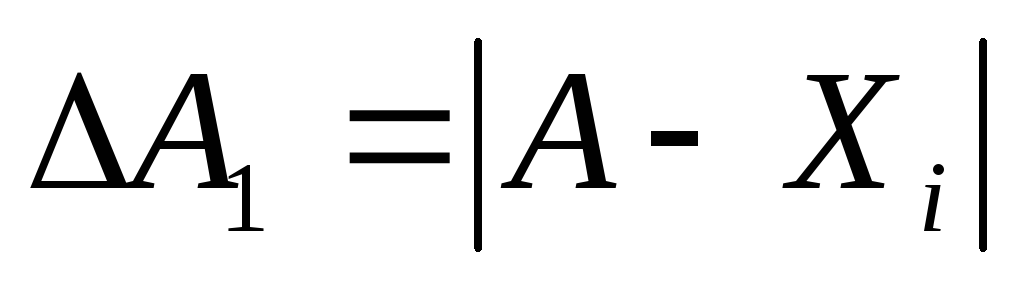(13)

Размерность
абсолютной ошибки совпадает с размерностью
определяемой величины. Относительной
ошибкой косвенных измерений называют
отвлечённое число:

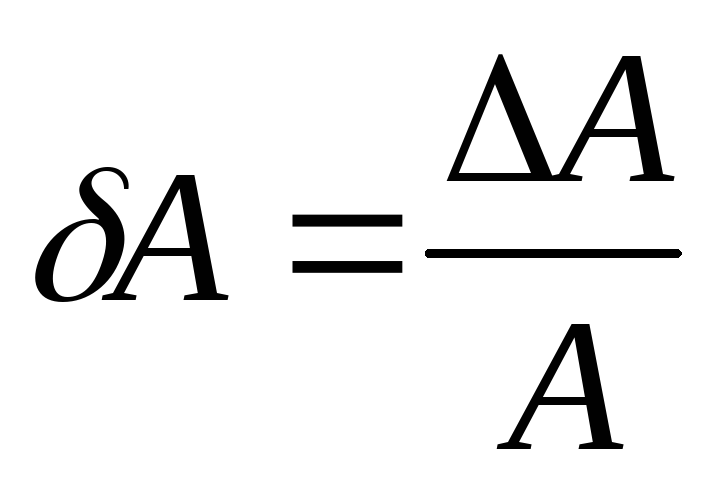(14)

Иногда относительную
ошибку выражают в процентах:

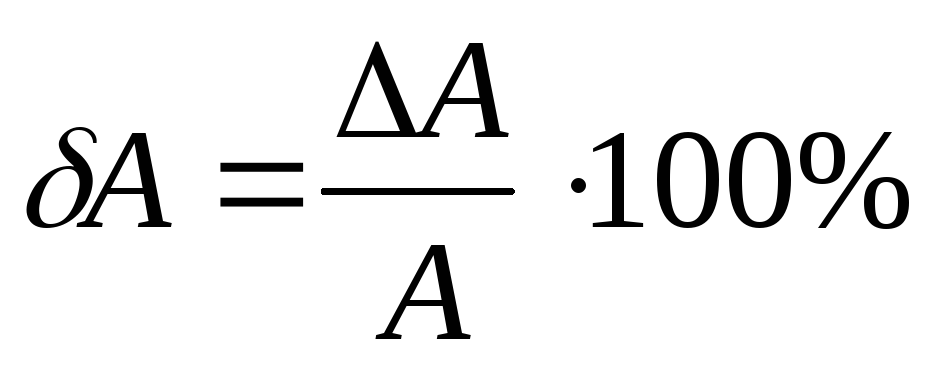(15)

Для определения
величины «А» в формулах (12)…(15) по
теории

вероятностей
следует брать величину Х, которую можно
определить двумя способами:

1) А
= Х
= (Х₁
+ Х₂
+…+Х_n)/n
(16)

2) A
= X
= f(x₁
+ x₂
+…+x_n)
(17)

где x₁,x₂
,…, x_n
определяют по формуле (3). Если ошибки
измерений малы, то оба способа дают
практически тождественные результаты.

Рассмотрим способы
нахождения ошибки величины А,
опреде­лённой из косвенных измерений,
по найденным значениям оши

бок прямых измерений.
Выше отмечалось, что возможны различные
соотношения между приборной систематической
и случайными ошибками.

1-й случай. Преобладают
приборные ошибки. В этом случае можно
дать только оценку максимальной ошибки.
Формулы для нахож­дения предельной
ошибки косвенных измерений по внешнему
виду совпадают с формулами дифференциального
исчисления. В связи с этим для предельной
абсолютной ошибки используется формула:

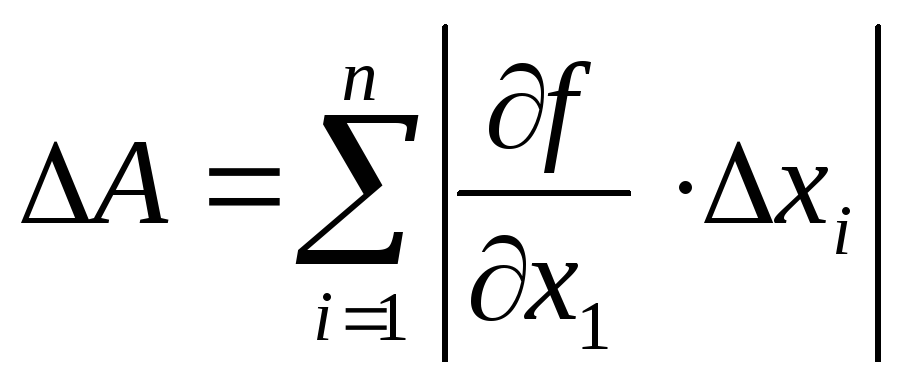(18)

а для расчёта
предельной относительной ошибки пригодна
фор

— 19 —

мула:

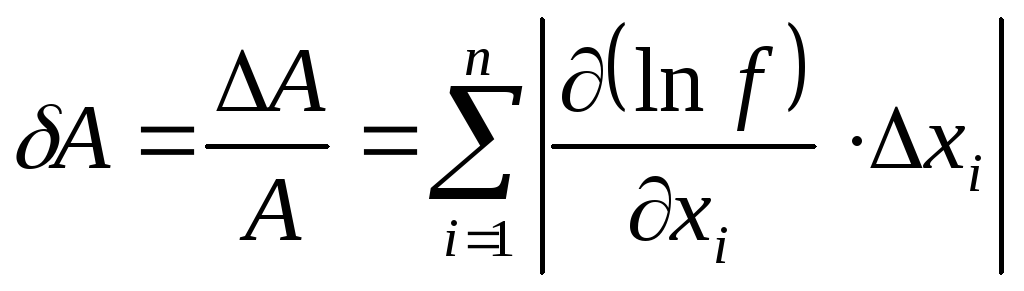(19)

Формулы для расчёта
предельных ошибок некоторых часто
встречающихся функций, когда приборные
ошибки превышают случайные, приведены
в Таблице 2. Эти выражения легко
рассчитываются по формулам (18) и (19).

2-й случай. Преобладают
случайные ошибки. Для определения
среднеквадратичной ошибки теория
вероятностей даёт следующую формулу:

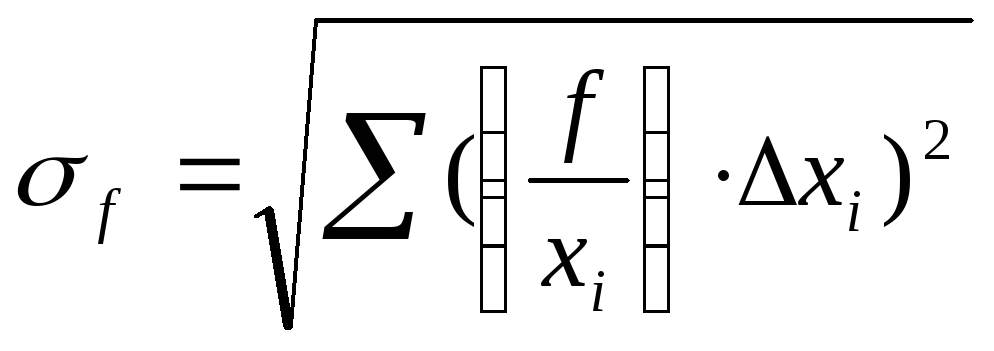(20)

Относительная
ошибка вычисляется по формуле:

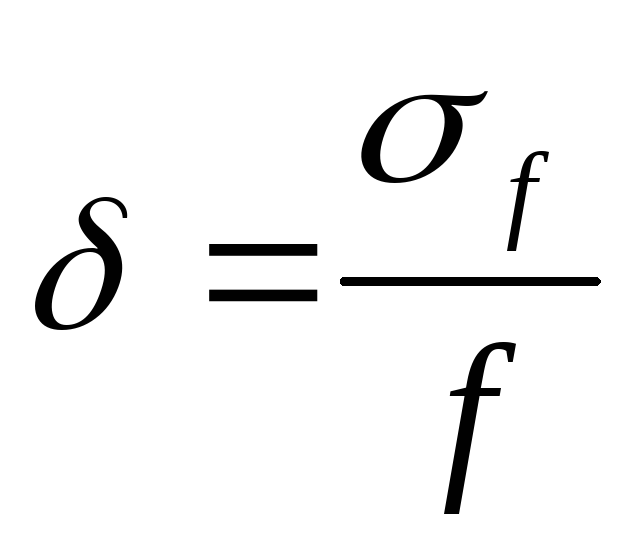(21)

При выполнении
промежуточных расчётов необходимо
помнить, что число точных цифр в результате
расчётов не может увеличиваться. Поэтому
промежуточные результаты округляют,
сохраняя

1…2 избыточных
знака. При этом последующие цифры,
меньшие

5,отбрасываются;если
первая из отбрасываемых цифр больше 5,

то последняя из
оставшихся цифр увеличивается на
единицу. Ес

ли первая
отбрасываемая цифра 5, то предыдущая
цифра остаётся

без изменений,
если она чётная, и увеличивается на
единицу, если

она нечётная.
Выражения для среднеквадратичной ошибки
некоторых часто встречающихся функций
приведены в Таблице 3. Для определения
ошибок косвенных измерений используют
большую из инструментальной или случайной
ошибок прямого измерения.

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

При многократном измерении одной и той же величины каждый раз получают несколько отличающиеся результаты, как по абсолютной величине, так и по знакам, каким бы опытом не обладал исполнитель и какими бы высокоточными приборами он не пользовался.
Погрешности различают: грубые, систематические и случайные.
Появление грубых погрешностей (промахов) связано с серьезными ошибками при производстве измерительных работ. Эти ошибки легко выявляются и устраняются в результате контроля измерений.Систематические погрешностивходят в каждый результат измерений по строго определенному закону. Они обусловлены влиянием конструкции измерительных приборов, погрешностями градуировки их шкал, износом и т. д. (инструментальные погрешности)иливозникают из-за недоучета условий измерений и закономерностей их изменений, приближенности некоторых формул и др. (методические погрешности). Систематические погрешности делятся на постоянные (неизменные по знаку и вели чине) и переменные (изменяющие свою величину от одного измерения к другому по определенному закону).
Такие погрешности заранее определимы и могут быть сведены к необходимому минимуму путем введения соответствующих поправок.Например, заранее может быть учтено влияние кривизны Земли на точность определения вертикальных расстояний, влияние температуры воздуха и атмосферного давления при определении длин линий светодальномерами или электронными тахеометрами, заранее можно учесть влияние рефракции атмосферы и т. д.
Если не допускать грубых погрешностей и устранять систематические, то качество измерений будет определяться только случайными погрешностями. Эти погрешности неустранимы, однако их поведение подчиняется законам больших чисел. Их можно анализировать, контролировать и сводить к необходимому минимуму.
Для уменьшения влияния случайных погрешностей на результаты измерений прибегают к многократным измерениям, к улучшению условий работы, выбирают более совершенные приборы, методы измерений и осуществляют тщательное их производство.
Сопоставляя ряды случайных погрешностей равноточных измерений можно обнаружить, что они обладают следующими свойствами:
а) для данного вида и условий измерений случайные погрешности не могут превышать по абсолютной величине некоторого предела;
б) малые по абсолютной величине погрешности появляются чаще больших;
в) положительные погрешности появляются так же часто, как и равные им по абсолютной величине отрицательные;
г) среднее арифметическое из случайных погрешностей одной и той же величины стремится к нулю при неограниченном увеличении числа измерений.
Распределение ошибок, соответствующее указанным свойствам, называется нормальным (рис. 12.1).

Рис. 12.1. Кривая нормального распределения случайных погрешностей Гаусса

Разность между результатом измерения некоторой величины (l) и ее истинным значением (X) называют абсолютной (истинной) погрешностью.

Δ = l — X

Истинное (абсолютно точное) значение измеряемой величины получить невозможно, даже используя приборы самой высокой точности и самую совершенную методику измерений. Лишь в отдельных случаях может быть известно теоретическое значение величины. Накопление погрешностей приводит к образованию расхождений между результатами измерений и действительными их значениями.Разность суммы практически измеренных (или вычисленных) величин и теоретического ее значения называется невязкой. Например, теоретическая сумма углов в плоском треугольнике равна 180º, а сумма измеренных углов оказалась равной 180º02′; тогда погрешность суммы измеренных углов составит +0º02′. Эта погрешность будет угловой невязкой треугольника.
Абсолютная погрешность не является, полным показателем точности выполненных работ. Например, если некоторая линия, фактическая длина которой составляет 1000 м, измерена землемерной лентой с ошибкой 0,5 м, а отрезок длиною 200 м  – с ошибкой 0,2 м, то, несмотря на то, что абсолютная погрешность первого измерения больше второго, все же первое измерение было выполнено с точностью в два раза более высокой. Поэтому вводят понятие относительной погрешности:

Отношение абсолютной погрешности измеряемой величины Δ к измеренной величине l называют относительной погрешностью.

Относительные погрешности всегда выражаются дробью с числителем, равным единице (аликвотная дробь). Так, в приведенном выше примере относительная погрешность первого измерения составляет

,

а второго 

30 Поверка и калибровка си. Определения. Правовые основы.

В
соответствии с законом РК «Об обеспечении
единства измерений» введе­ны следующие
понятия:

— поверка
средства измерений —
совокупность операций, выполняемых
органа­ми Государственной метрологической
службы (другими уполномоченными на то
органами, организациями) с целью
определения и подтверждения соответ­ствия
средства измерений установленным
требованиям;

— калибровка
средств измерений —
совокупность операций, выполняемых с
це­лью определения и подтверждения
действительных значений метрологических
характеристик и/или пригодности к
применению средства измерений, не
под­лежащего государственному
метрологическому контролю и надзору.

В
обоих случаях, как при поверке, так и
при калибровке, определяются метрологические
характеристики средств измерений,
причем часто по одной и той же методике,
называемой методикой
поверки,
но на этом их сходство заканчивается. Различия
между этими понятиями имеют
более принципиальный характер.

Во-первых,
в сферах распространения ГМКиН могут
применяться только поверенные СИ, а
калиброванные — не могут.

Во-вторых,
поверке могут подвергаться только СИ
утверж­денного типа, то есть внесенные
в Государственный реестр СИ, а калибровке
— любые, в том числе нестандартизованные
и изготовленные в од­ном экземпляре.

В-третьих,
при поверке проверяется соответствие
СИ своему типу, внесенному в Государственный
реестр, тогда как при калибровке
опреде­ляются действительные
метрологические характеристики, которые
прибор име­ет на момент калибровки.

Если
при поверке СИ обнаружено его несоответствие
хотя бы одному пункту утвержденного
типа, средство измерений должно быть
забраковано. При калибровке этому СИ
будут приписаны новые значения
метро­логических характеристик.

Положительные
результаты поверки удостоверяются
поверительным клеймом или свидетельством
о поверке. Если средство измерений по
результатам поверки признано непригодным
к применению, оттиск поверительного
клейма и свиде­тельство о поверке
аннулируются и выписывается извещение
о непригодности или делаются соответствующие
записи в технической документации.

Результаты
калибровки удостоверяются калибровочным
знаком (клеймом), наносимым на средство
измерений, или сертификатом о калибровке,
а также, записью в эксплуатационных
документах. В соответствии с законом
РК «Об обеспечении единства измерений»
калибровка средств измерений является
процедурой добровольной и осуществляемой
по желанию владельца прибора с це­лью,
например, получения достоверных
результатов измерений, влияющих, в
конечном счете, на результаты труда.
ГМКиН на такие средства измерений не
распространяется.

Относительная погрешность измерения ε (ЭПСИЛОН)

Иногда важно знать, какую часть составляет наша погрешность от значения  измеряемой величины. Для этого разделим 0,5 мм на 706 мм

В результате получим: .  То есть наша ошибка составляет 0,0007 долю ширины стола, или 0,0007 · 100% = 0,07%. Это свидетельствует о достаточно высокой точности измерения. Эту погрешность называют относительной и обозначают греческой буквой  (эпсилон): 

     (5.1)

Относительная погрешность измерения свидетельствует о качестве измерения. Если длина какогото предмета равна 5 мм, а точность измерения –  плюс-минус 0,5 мм, то относительная погрешность будет составлять уже 10%.

Стандартная запись результата измерений и выводы

Таким образом, абсолютная погрешность в примере 5.1. составляет ∆L = 0,5 мм, а результат измерений следует записать в стандартном виде: L = (706,0 0,5) мм — Опыт выполнен с относительной погрешностью 0,0007 или 0,07%.

На точность измерения влияет много факторов, в частности:

1. При совмещении края стола с делением шкалы рулетки мы неминуемо допускаем погрешность, поскольку делаем это «на глаз» — смотреть можно под разными углами.
2. Не вполне ровно установили рулетку.
3. Наша рулетка является копией эталона и может несколько отличаться от оригинала.

Все это необходимо учитывать при проведении измерений.

Итоги:

• Измерения в физике всегда неточны, и надо знать пределы погрешности измерений, чтобы понимать, насколько можно доверять результатам.
• Абсолютную погрешность измерения можно определить как половину цены деления шкалы измерительного прибора. 
• Относительная погрешность есть частное от деления абсолютной погрешности на значение измеряемой величины:   и указывает на качество измерения. Ее можно выразить в процентах.