Расчет случайной погрешности

Введение

Все, что сказано в этом введении, запоминать не нужно. это справочный материал, к которому вы будете обращаться при выполнении лабораторных работ.

1. Как определять погрешности измерений

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

A, B, C, … — физические величины.

A_пр — приближенное значение физической величины, т.е. значение, полученное путем прямых или косвенных измерений.

ΔA — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

Δ_иA — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; указывается в каждой работе при описании прибора в разделе Оборудование и средства измерения)

Δ_оA — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения), она равна в большинстве случаев половине цены деления; при измерении времени — цене деления секундомера или часов.

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

ΔA=Δ_иA + Δ_оA

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔA≈0,17=0,2); численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А=10,332≈10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, отличаются друг от друга.

В этом случае A_пр находят как среднее арифметическое значение всех измерений, а ΔA (ее в этом случае называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. При этом для получения результата достаточно одного измерения.

Относительная погрешность косвенных измерений определяется, как показано в таблице 1.

Абсолютная погрешность косвенных измерений определяется по формуле ΔA=A_прε (ε выражается десятичной дробью).

Таблица 1

Формулы для нахождения относительной погрешности косвенных измерений

Nº п/п	Формула физической величины	Формула относительной погрешности
1
2
3	A=B+C
4

2. О классе точности электроизмерительных приборов

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ_пр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность Δ_иA от всей шкалы прибора (A_max):

Класс точности указывается при описании прибора в разделе Оборудование и средства измерения. Cуществуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ_пр) и всю его шкалу (A_max), определяют абсолютную погрешность Δ_иA измерения физической величины А этим прибором:

3. Как сравнивать результаты измерений

1. Записать результаты измерений в виде двойных неравенств:

A_{1 пр} – ΔA₁ < A_{1 пр} < A_{1 пр} + ΔA₁A_{2 пр} – ΔA₂ < A_{2 пр} < A_{2 пр} + ΔA₂
2. Сравнить полученные интервалы значений (рис.1): если интервалы не перекрываются, то результаты неодинаковы, если перекрываются — одинаковы при данной относительной погрешности измерений.

Рисунок 1.

4. Как оформлять отчет о проделанной работе

Отчетом о проделанной работе является форма, находящаяся в левом нижнем окне. После ее заполнения надо нажать на кнопку «Отправить результаты на сервер».

Значения измеренных физических величин переносятся в таблицу результатов автоматически после нажатия соответствующей кнопки.

Значения остальных величин и ответ на контрольный вопрос вводятся с клавиатуры.

домашней странице BARSIC

Значения коэффициентов Стьюдента

Формула для расчета абсолютной погрешности n δ	0,9	0,95	0,99	0,999
1	2	3	4	5
2 3 4 5 6 7 8 9 10 ∞	6,31 2,92 2,35 2,13 2,02 1,94 1,90 1,86 1,83 1,65	12,71 4,30 3,18 2,78 2,57 2,45 2,36 2,31 2,26 1,96	63,66 9,92 5,84 4,60 4,03 3,71 3,50 3,36 3,25 2,58	636,62 31,60 12,84 8,61 6,86 5,96 5,40 5,04 4,78 3,29

Например,
задавая доверительную вероятность δ
=0.95, по числу проведенных измерений n=5
по табл. 2 можно найти
=
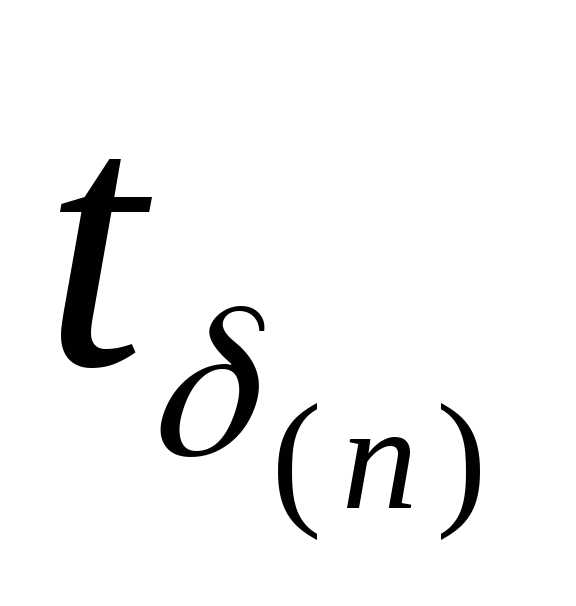2,78. Тогда, определив предварительно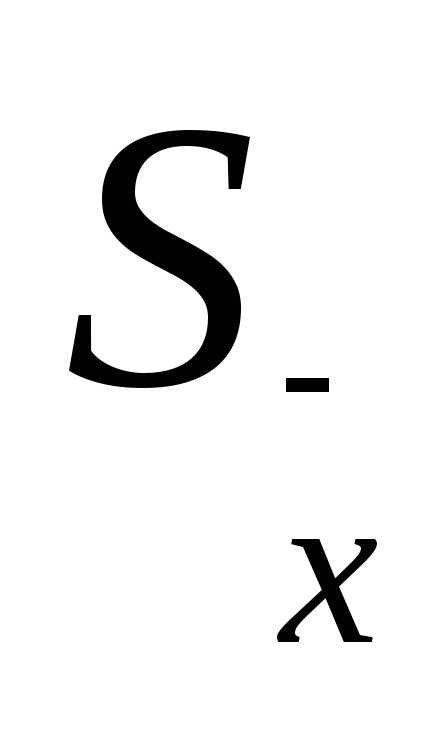по формуле (35), найдем погрешность ∆X:

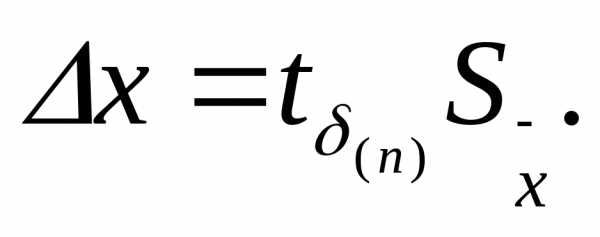(41)

Выражение
(41) ввиду малого объема информации дает
границы доверительного интервала более
широкими.

Результат
измерения можно представить в виде:

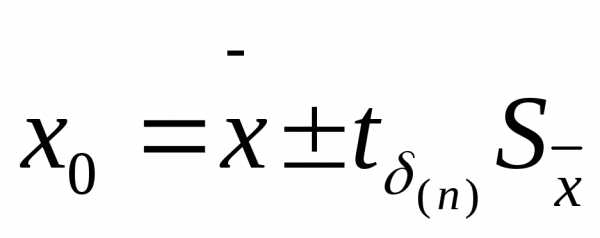при
δ=0,95, n=5.
(42)

Конечно,
оценка (42) еще не дает представления об
общей погрешности измерения, в
которую
входит и систематическая ошибка.

Совместный
учет случайных
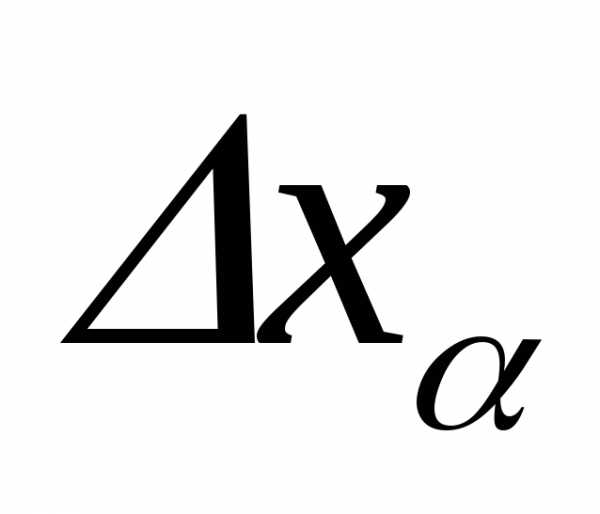и систематических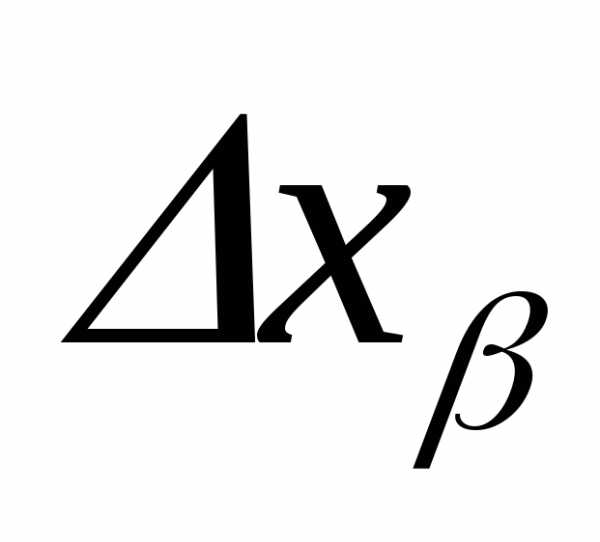ошибок можно произвести по формуле

При
этом следует принять во внимание, что
всегда имеет максимальное значение.
Максимальное же значение случайных
ошибок равно 3σ. Следовательно, для их
равноправного учета необходимо
предположить, что приборная погрешность
β (или ∆пр)
равна утроенной дисперсии распределения
погрешностей прибора 3σпр
,т.е

погрешности соответствующей
надежности δ =0.997. Тогда за систематическую
ошибку можно принять
и общая погрешность выразитсясоотношением

(43)

Коэффициенты
Стьюдента для проведенного числа
измерений
и бесконечного числа измеренийнаходят по табл.2 для одной и той же
заданной надежностиδ.

Погрешности косвенных измерений

Часто
приходится вычислять искомую величину
по результатам измерений других величин,
связанных с этой величиной определенной
функциональной зависимостью. Например,
объем шара
можно вычислить, измерив его радиусR
. Также измерения называются косвенными.

Рассмотрим
конкретный пример. Допустим, что величины
Х,
У
и U
связаны равенством

.
(44)

Непосредственно
измеряются величины Х
и У,
и по этим измерениям мы судим об U,
считая

(45)

измерением
величины U.

Предполагается,
что измерения Х_i
и y_i
независимы друг

от
друга, и распределены нормально с
дисперсиям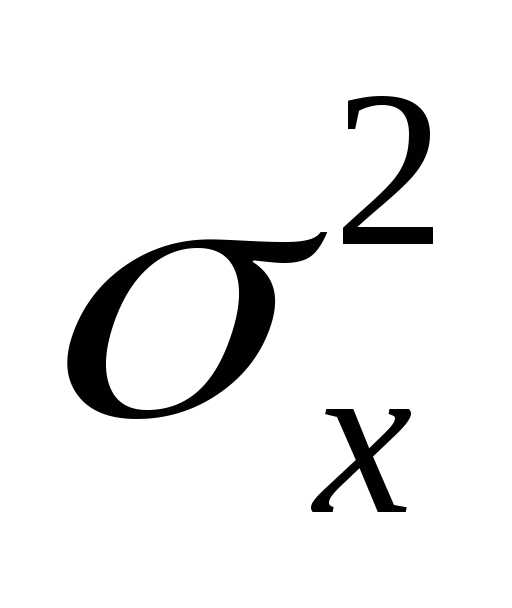и
и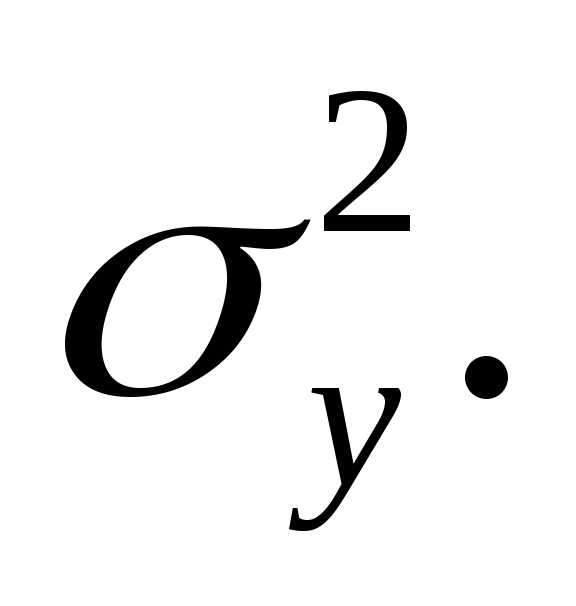Задача
заключается в том, как по известным
значениям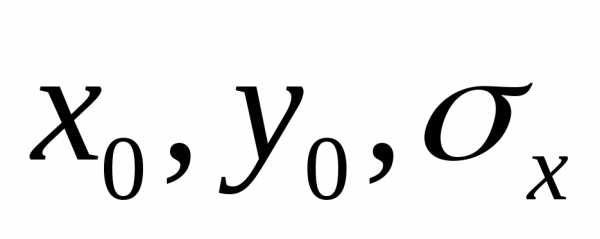иопределить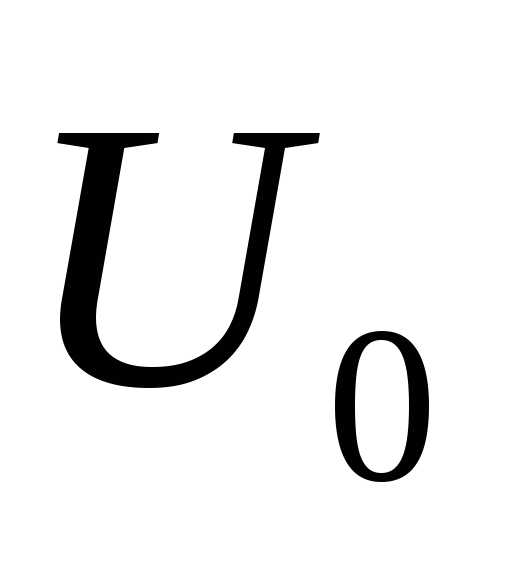и.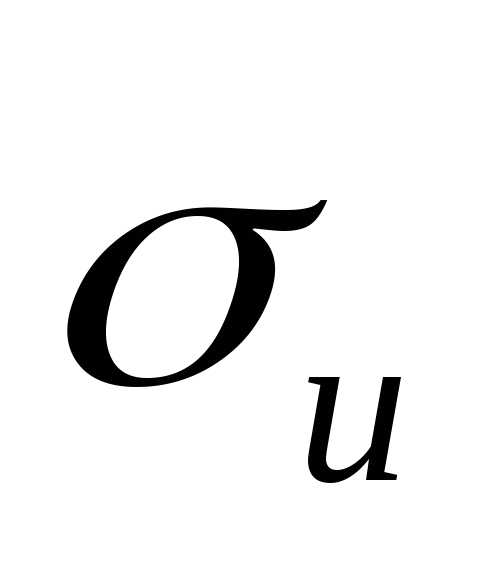

Очевидно,
что погрешность косвенного измерения
обусловлена
погрешностями отдельных измерений
и.
Поэтому выражение (45) можно переписать
в виде:

(46)

Вычитая
почленно левые и правые части уравнений
(46) и (44). для погрешности косвенного
измерения получим:

(47)

Тогда
для дисперсии результатов косвенного
измерения можно записать выражение:

Здесь
член
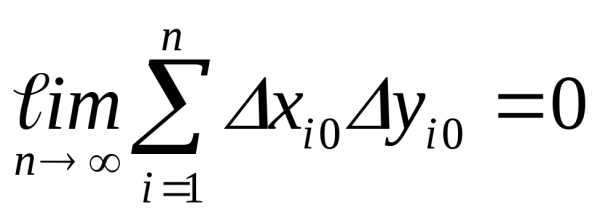, так как любое произведение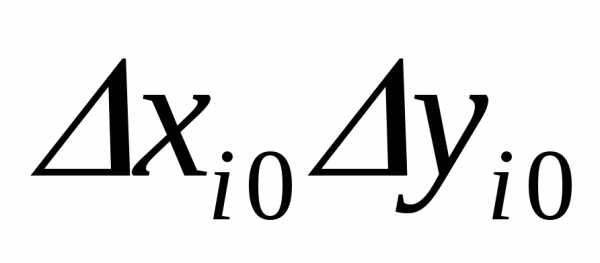может быть с равной вероятностью или
положительным, или отрицательным.

Учитывая,
что
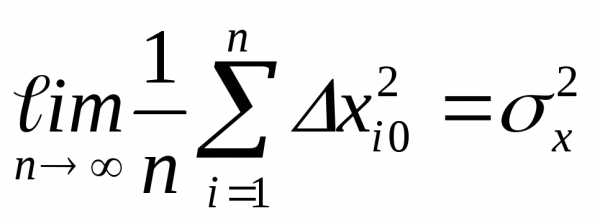и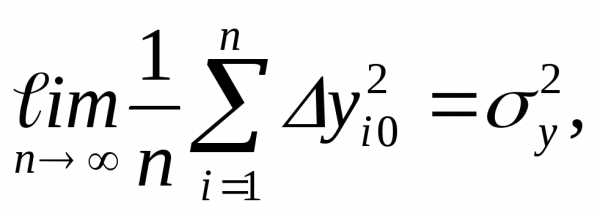

получим

(48)

или
(49)

Равенство
(49) определяет соотношение средних
квадратичных ошибок прямых и косвенных
измерений. Это выражение для частного
случая имеет весьма общий характер и
называется законом сложения дисперсий.

Следовательно,
при измерении нескольких неизвестных
величин складываются дисперсии этих
величин (не ошибки, а именно дисперсии).

Средние
квадратичные ошибки средних арифметических
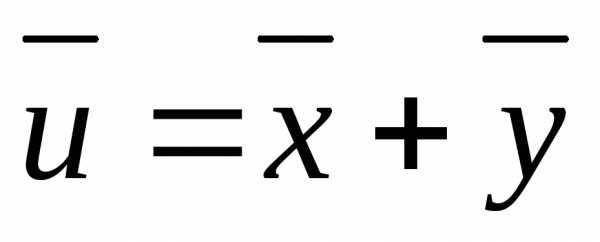связаны
аналогичным образом

(50)

Рассмотрим
общий случай, когда u
— функция двух переменных х и y:

(51)

Ошибки
в величинах х и у такова:
,
где Х
и У
— истинные значения величин Х в У. Тогда
для результата отдельного измерения
можно записать

(52)

Если
‘та функция непрерывна и имеет
производные, то ее можно разложить в
ряд Тейлора. Рассматривая только члены
c
нулевыми и первыми степенями малых
погрешностей
и,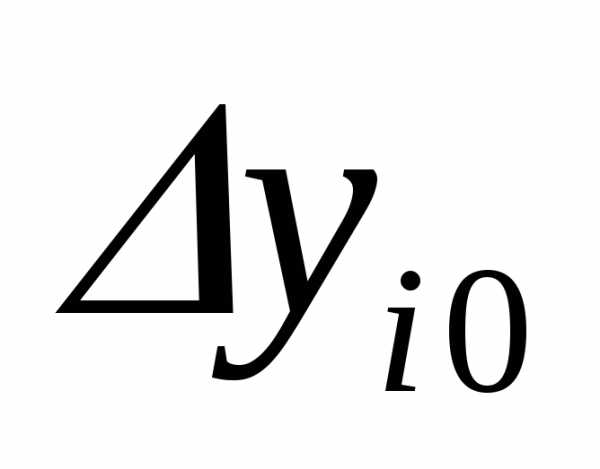
получим:

или
поскольку

(53)

Частные
производные здесь вычисляются при Х=Х
и У=У.
Запишем выражение для дисперсии
результатов косвенного измерения:

Учитывая,
что

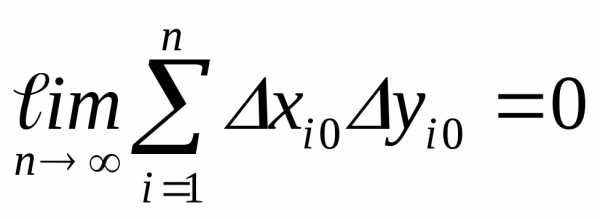и

получим

(54)

или

(55)

Для
относительной погрешности косвенного
измерения

учитывая,
что
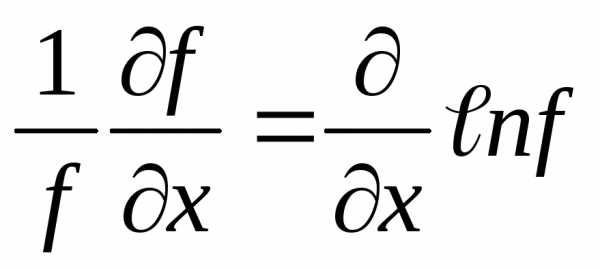и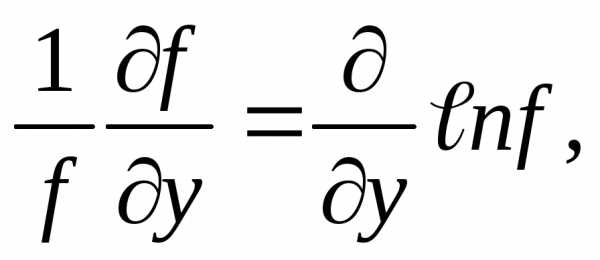получим:

(56)

4.4.5. Дополнительные погрешности

Дополнительные погрешности задаются в виде функции влияния внешних факторов (температуры, влажности, напряжения питания) на основную погрешность измерения или, в случае линейной функции влияния, коэффициентом влияния. Например, может быть задано, что основная погрешность увеличивается на +0,05% при изменении напряжения питания на +20%.

Если задан диапазон изменения влияющих величин, в качестве их математического ожидания для расчетов с помощью функции влияния берут их среднее значение [].

Среднеквадратическое отклонение дополнительной погрешности для линейной функции влияния находят по формуле []

,

(4.108)

где — коэффициент влияния внешнего фактора; — нижняя и верхняя граница изменения влияющей величины.

Дополнительная погрешность может увеличивать как систематическую, так и случайную составляющую основной погрешности. Для этого функции влияния задаются раздельно на каждую составляющую.

Если известно, что дополнительные погрешности нескольких средств измерений коррелируют (например, синхронно возрастают при увеличении напряжения питания в сети или температуры окружающей среды), то такие погрешности суммируют как коррелированные величины, с учетом коэффициента корреляции (4.102) — (4.104).

Дополнительные погрешности считаются несущественными, если их сумма составляет менее 17% от наибольшего возможного значения инструментальной погрешности в рабочих условиях эксплуатации [].

Понятие о неравноточных измерениях

_______Неравноточными измерениями называются такие, которые выполнены различным
числом приемов, приборами различной точности и т.д.
Если измерения неодинаковой точности, то для определения общей арифметической
середины пользуются формулой:

где p₁, p₂, p₃, ……..p_n — соответствующие веса неравноточных измерений l₁, l₂, l₃,……. l _n

________Весом называется число, которое выражает степень доверия к результату измерения. В тех случаях, когда неизвестны веса измеренных величин, а известны их средние
квадратические ошибки, то веса можно вычислить по формуле:

_______При неравноточных измерениях средняя квадратическая ошибка измерения, вес
которого равен единице, определяется по формуле:

где δ – разность между отдельными результатами измерений и общей арифметической
серединой.

4.4.1. Исходные данные для расчета

Исходными данными для расчета погрешности измерительных каналов являются ([]):

• метрологические характеристики средств измерений;
• погрешность метода измерений (методическая погрешность);
• характеристики влияющих величин (например, окружающая температура, влажность);
• характеристики измеряемого сигнала.

ГОСТ 8.009 [] для всех типов средств измерений устанавливает следующий комплекс метрологических характеристик, который указывается в эксплуатационной документации на средства измерений:

• систематическая составляющая основной погрешности;
• среднеквадратическое отклонение случайной составляющей основной погрешности;
• дополнительная погрешность для каждой из влияющих величин;
• динамическая погрешность.

Некоторые средства измерений обладают гистерезисом — для них кроме перечисленных погрешностей указывается случайная составляющая основной погрешности, вызванной гистерезисом.

Основная погрешность может быть указана без разделения ее на части (на систематическую, случайную и погрешность от гистерезиса), и этот вариант является наиболее распространенным. Случайную составляющую указывают в случае, когда она больше 10% от систематической [].

Дополнительная погрешность указывается в виде функции влияния внешнего фактора на основную погрешность или ее составляющие: систематическую и случайную. Обычно эта функция представляет собой линейную зависимость и тогда указывается только коэффициент влияния, например, 0,05%/ºС.

Динамическая погрешность указывается с помощью одной из следующих характеристик: импульсная, переходная, амплитудно-частотная и фазочастотная, амплитудно-фазовая характеристика, передаточная функция. Для минимально-фазовых цепей указывается только ампитудно-частотная характеристика, поскольку фазо-частоная однозначно может быть получена из амплитудно-частотной характеристики.

Для расчета методической погрешности могут быть указаны сопротивления проводов, среднеквадратическое значение или спектральная плотность помех в них, емкость, индуктивность и сопротивление источника сигнала, а также другие факторы, которые возникают при создании системы, включающей средства и объект измерений.

Характеристики измеряемого сигнала задаются в виде функции от времени или функции спектральной плотности. Для случайного входного сигнала задается спектральная плотность мощности или автокорреляционная функция. Во многих случаях для оценки погрешности бывает достаточно знания скорости нарастания входного сигнала.

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

При многократном измерении одной и той же величины каждый раз получают несколько отличающиеся результаты, как по абсолютной величине, так и по знакам, каким бы опытом не обладал исполнитель и какими бы высокоточными приборами он не пользовался.
Погрешности различают: грубые, систематические и случайные.
Появление грубых погрешностей (промахов) связано с серьезными ошибками при производстве измерительных работ. Эти ошибки легко выявляются и устраняются в результате контроля измерений.Систематические погрешностивходят в каждый результат измерений по строго определенному закону. Они обусловлены влиянием конструкции измерительных приборов, погрешностями градуировки их шкал, износом и т. д. (инструментальные погрешности)иливозникают из-за недоучета условий измерений и закономерностей их изменений, приближенности некоторых формул и др. (методические погрешности). Систематические погрешности делятся на постоянные (неизменные по знаку и вели чине) и переменные (изменяющие свою величину от одного измерения к другому по определенному закону).
Такие погрешности заранее определимы и могут быть сведены к необходимому минимуму путем введения соответствующих поправок.Например, заранее может быть учтено влияние кривизны Земли на точность определения вертикальных расстояний, влияние температуры воздуха и атмосферного давления при определении длин линий светодальномерами или электронными тахеометрами, заранее можно учесть влияние рефракции атмосферы и т. д.
Если не допускать грубых погрешностей и устранять систематические, то качество измерений будет определяться только случайными погрешностями. Эти погрешности неустранимы, однако их поведение подчиняется законам больших чисел. Их можно анализировать, контролировать и сводить к необходимому минимуму.
Для уменьшения влияния случайных погрешностей на результаты измерений прибегают к многократным измерениям, к улучшению условий работы, выбирают более совершенные приборы, методы измерений и осуществляют тщательное их производство.
Сопоставляя ряды случайных погрешностей равноточных измерений можно обнаружить, что они обладают следующими свойствами:
а) для данного вида и условий измерений случайные погрешности не могут превышать по абсолютной величине некоторого предела;
б) малые по абсолютной величине погрешности появляются чаще больших;
в) положительные погрешности появляются так же часто, как и равные им по абсолютной величине отрицательные;
г) среднее арифметическое из случайных погрешностей одной и той же величины стремится к нулю при неограниченном увеличении числа измерений.
Распределение ошибок, соответствующее указанным свойствам, называется нормальным (рис. 12.1).

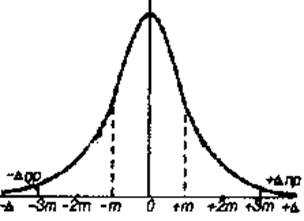Рис. 12.1. Кривая нормального распределения случайных погрешностей Гаусса

Разность между результатом измерения некоторой величины (l) и ее истинным значением (X) называют абсолютной (истинной) погрешностью.

Δ = l — X

Истинное (абсолютно точное) значение измеряемой величины получить невозможно, даже используя приборы самой высокой точности и самую совершенную методику измерений. Лишь в отдельных случаях может быть известно теоретическое значение величины. Накопление погрешностей приводит к образованию расхождений между результатами измерений и действительными их значениями.Разность суммы практически измеренных (или вычисленных) величин и теоретического ее значения называется невязкой. Например, теоретическая сумма углов в плоском треугольнике равна 180º, а сумма измеренных углов оказалась равной 180º02′; тогда погрешность суммы измеренных углов составит +0º02′. Эта погрешность будет угловой невязкой треугольника.
Абсолютная погрешность не является, полным показателем точности выполненных работ. Например, если некоторая линия, фактическая длина которой составляет 1000 м, измерена землемерной лентой с ошибкой 0,5 м, а отрезок длиною 200 м  – с ошибкой 0,2 м, то, несмотря на то, что абсолютная погрешность первого измерения больше второго, все же первое измерение было выполнено с точностью в два раза более высокой. Поэтому вводят понятие относительной погрешности:

Отношение абсолютной погрешности измеряемой величины Δ к измеренной величине l называют относительной погрешностью.

Относительные погрешности всегда выражаются дробью с числителем, равным единице (аликвотная дробь). Так, в приведенном выше примере относительная погрешность первого измерения составляет

,

а второго 

30 Поверка и калибровка си. Определения. Правовые основы.

В
соответствии с законом РК «Об обеспечении
единства измерений» введе­ны следующие
понятия:

— поверка
средства измерений —
совокупность операций, выполняемых
органа­ми Государственной метрологической
службы (другими уполномоченными на то
органами, организациями) с целью
определения и подтверждения соответ­ствия
средства измерений установленным
требованиям;

— калибровка
средств измерений —
совокупность операций, выполняемых с
це­лью определения и подтверждения
действительных значений метрологических
характеристик и/или пригодности к
применению средства измерений, не
под­лежащего государственному
метрологическому контролю и надзору.

В
обоих случаях, как при поверке, так и
при калибровке, определяются метрологические
характеристики средств измерений,
причем часто по одной и той же методике,
называемой методикой
поверки,
но на этом их сходство заканчивается. Различия
между этими понятиями имеют
более принципиальный характер.

Во-первых,
в сферах распространения ГМКиН могут
применяться только поверенные СИ, а
калиброванные — не могут.

Во-вторых,
поверке могут подвергаться только СИ
утверж­денного типа, то есть внесенные
в Государственный реестр СИ, а калибровке
— любые, в том числе нестандартизованные
и изготовленные в од­ном экземпляре.

В-третьих,
при поверке проверяется соответствие
СИ своему типу, внесенному в Государственный
реестр, тогда как при калибровке
опреде­ляются действительные
метрологические характеристики, которые
прибор име­ет на момент калибровки.

Если
при поверке СИ обнаружено его несоответствие
хотя бы одному пункту утвержденного
типа, средство измерений должно быть
забраковано. При калибровке этому СИ
будут приписаны новые значения
метро­логических характеристик.

Положительные
результаты поверки удостоверяются
поверительным клеймом или свидетельством
о поверке. Если средство измерений по
результатам поверки признано непригодным
к применению, оттиск поверительного
клейма и свиде­тельство о поверке
аннулируются и выписывается извещение
о непригодности или делаются соответствующие
записи в технической документации.

Результаты
калибровки удостоверяются калибровочным
знаком (клеймом), наносимым на средство
измерений, или сертификатом о калибровке,
а также, записью в эксплуатационных
документах. В соответствии с законом
РК «Об обеспечении единства измерений»
калибровка средств измерений является
процедурой добровольной и осуществляемой
по желанию владельца прибора с це­лью,
например, получения достоверных
результатов измерений, влияющих, в
конечном счете, на результаты труда.
ГМКиН на такие средства измерений не
распространяется.

Расчёт ошибок косвенных измерений

Пусть искомая
величина Апри выбранном
методе косвенных измерений рассчитывается
по формуле:

A
= f(x₁
,x₂
,x₃
,…,x_n
) (12)

где x₁,x₂,…,x_n
— величины, найденные в результате прямых
измерений, с учётом ошибок о которых
шла речь выше. Из-за этих ошибок величина
«А»
так же будет определяться с ошибками.

Пусть X₁,X₂,…,X_N
— значения f(x₁
,x₂
,x₃
,…,x_n), вычисленные
для разных серий измерений (x₁,x₂,…,x_n).

Таблица 1

Таблица коэффициентов
Стьюдента

Число измерений	Доверительная вероятность
0.7	0.8	0.9	0.95	0.99	0.999
2	2.0	3.1	6.3	12.7	63.7	636.6
3	1.3	1.9	2.9	4.3	9.9	31.6
4	1.3	1.6	2.4	3.2	5.8	12.9
5	1.2	1.5	2.1	2.8	4.6	8.6
10	1.1	1.4	1.8	2.3	3.3	4.8
15	1.1	1.3	1.8	2.1	3.0	4.1
20	1.1	1.3	1.7	2.1	2.9	3.9

Абсолютной ошибкой
косвенных измерений, по аналогии с
аб­солютной ошибкой прямых измерений,
называют разность между ис­тинным
значением «А» и её значениями,
полученными в результате измерений:

(13)

Размерность
абсолютной ошибки совпадает с размерностью
определяемой величины. Относительной
ошибкой косвенных измерений называют
отвлечённое число:

(14)

Иногда относительную
ошибку выражают в процентах:

(15)

Для определения
величины «А» в формулах (12)…(15) по
теории

вероятностей
следует брать величину Х, которую можно
определить двумя способами:

1) А
= Х
= (Х₁
+ Х₂
+…+Х_n)/n
(16)

2) A
= X
= f(x₁
+ x₂
+…+x_n)
(17)

где x₁,x₂
,…, x_n
определяют по формуле (3). Если ошибки
измерений малы, то оба способа дают
практически тождественные результаты.

Рассмотрим способы
нахождения ошибки величины А,
опреде­лённой из косвенных измерений,
по найденным значениям оши

бок прямых измерений.
Выше отмечалось, что возможны различные
соотношения между приборной систематической
и случайными ошибками.

1-й случай. Преобладают
приборные ошибки. В этом случае можно
дать только оценку максимальной ошибки.
Формулы для нахож­дения предельной
ошибки косвенных измерений по внешнему
виду совпадают с формулами дифференциального
исчисления. В связи с этим для предельной
абсолютной ошибки используется формула:

(18)

а для расчёта
предельной относительной ошибки пригодна
фор

— 19 —

мула:

(19)

Формулы для расчёта
предельных ошибок некоторых часто
встречающихся функций, когда приборные
ошибки превышают случайные, приведены
в Таблице 2. Эти выражения легко
рассчитываются по формулам (18) и (19).

2-й случай. Преобладают
случайные ошибки. Для определения
среднеквадратичной ошибки теория
вероятностей даёт следующую формулу:

(20)

Относительная
ошибка вычисляется по формуле:

(21)

При выполнении
промежуточных расчётов необходимо
помнить, что число точных цифр в результате
расчётов не может увеличиваться. Поэтому
промежуточные результаты округляют,
сохраняя

1…2 избыточных
знака. При этом последующие цифры,
меньшие

5,отбрасываются;если
первая из отбрасываемых цифр больше 5,

то последняя из
оставшихся цифр увеличивается на
единицу. Ес

ли первая
отбрасываемая цифра 5, то предыдущая
цифра остаётся

без изменений,
если она чётная, и увеличивается на
единицу, если

она нечётная.
Выражения для среднеквадратичной ошибки
некоторых часто встречающихся функций
приведены в Таблице 3. Для определения
ошибок косвенных измерений используют
большую из инструментальной или случайной
ошибок прямого измерения.

4.4.3. Систематические погрешности

В наиболее типовом случае систематические составляющие основных погрешностей средств измерений суммируются геометрически, по формулам (4.30), (4.101), поскольку они являются случайными величинами.

Формулы геометрического суммирования были получены для среднеквадратических погрешностей (см. (4.25)). Поэтому, если комплекс метрологических характеристик средств измерений включает предел допускаемых значений систематической составляющей основной погрешности без указания среднеквадратического значения (по ГОСТ 8.009 []), то соответствующую ему среднеквадратическое значение находят, в соответствии с рекомендациями РД 50-453-84 [], по формуле

.

(4.105)

Эта формула справедлива, если нет оснований полагать, что функция распределения данной погрешности является несимметричной и имеет несколько максимумов.

Метрологическая инструкция МИ 2232-2000 [] рекомендует иную формулу — половину предела допускаемой погрешности.

Выбор способа суммирования систематических составляющих основных погрешностей не является однозначным и это связано с отсутствием полной информации о законе распределения. Дело в том, что причиной существования основной погрешности является как технологический разброс параметров электронных компонентов, так и нескомпенсированная нелинейность. Технологический разброс обычно является случайным и на этом основании систематическая составляющая погрешности может рассматриваться как случайная величина на множестве средств измерений одного и того же типа. Поэтому в формулах для расчета погрешностей она учитывается геометрически. Однако нелинейность передаточной характеристики средства измерений (нелинейность АЦП, нормирующих усилителей, термопар) у всех экземпляров приборов одного типа будет иметь примерно один и тот же вид, величину и знак. Например, погрешность, вызванная нелинейностью, в начале шкалы может быть положительной, в середине шкалы — отрицательной. у верхнего предела шкалы — опять положительной, и так для всех экземпляров приборов одного типа. Поэтому погрешности, обусловленные нелинейностью, должны суммироваться алгебраически.

В современных модулях аналогового ввода используется автоматическая калибровка, позволяющая уменьшить случайную компоненту систематической погрешности и в этом случае преобладающей является детерминированная погрешность нелинейности.

Поскольку ГОСТ 8.009 [] не предусматривает нормирование таких тонких нюансов поведения погрешностей, выбор способа суммирования начинает зависеть не от технических, а от политических факторов. Если фактическая погрешность окажется выше расчетной и это повлечет за собой угрозу жизни людей, большой экономический ущерб, техногенную катастрофу и т. п. [], то суммирование погрешностей выполняют алгебраически, причем используют не среднеквадратические отклонения, а пределы допустимых значений погрешности.

Если известен знак систематической погрешности, то его учитывают при суммировании.

Для наиболее ответственных применений следует использовать средства измерений, для которых указаны погрешность без разделения на случайную и систематическую компоненты, поскольку в этом случае погрешность указана с доверительной вероятностью, равной единице. Если же используются средства измерений, для которых указана случайная составляющая, то для них рассчитывают величину погрешности при доверительной вероятности, равной единице. Это условие существенно завышает требования к точности средства измерений.

Алгебраическое суммирование часто дает слишком завышенную оценку погрешности. Поэтому МИ 2232-2000 [] предусматривает промежуточный вариант между формулами геометрического и алгебраического суммирования:

,

(4.106)

где — поправочный коэффициент, равный 1,2 для наиболее важных параметров устройств аварийной защиты и блокировки, контроля за соблюдением требований техники безопасности и экологической безопасности, контроля характеристик готовой продукции [].

Для конкретных экземпляров приборов могут быть указаны не номинальные характеристики (имеющие одну и ту же величину для всех приборов данного типа), а индивидуальные. В этом случае систематическая погрешность является не случайной, а детерминированной величиной, поэтому должна учитываться в итоговой погрешности измерительного канала алгебраически.

Методики расчета

Существует несколько методов определения отклонения. Наиболее простой и доступный способ:

Необходимые измерения проводят не менее 5 раз. Это дает возможность вычислить наиболее точное значение параметра. Результаты вносят в таблицу excel.
Полученные величины складывают и делят на количество замеров. В результате получится действительное значение. Его обычно применяют вместо истинного, так как нет возможности вычислить последнее.
Следующий шаг — определение абсолютной погрешности. Ее считают для каждого измерения. Чтобы узнать величину этого показателя, из результата каждого замера вычитают действительное значение

Для обработки данных неважно, положительная или отрицательная получилась цифра. Используют модули полученных чисел, пренебрегая знаками.
Чтобы определить относительную погрешность измерения, нужно разделить абсолютную на действительное значение. Полученное число умножают на 100%.

Полученное число умножают на 100%.

Для определения предельного отклонения выбирают наибольшее значение из всех полученных.

Чтобы получить наиболее точные показатели дискретности цифровых приборов, пользуются средним квадратическим отклонением. Вычислить его можно следующим способом:

1. Каждый показатель абсолютной погрешности возводят в квадрат и записывают.
2. Полученные результаты складывают между собой.
3. Сумму всех квадратов делят на число, которое на единицу меньше количества измерений.
4. Из результата вычислений извлекают квадратный корень — это и будет среднее квадратическое отклонение.

Чтобы вычислить, чему равна относительная погрешность измерения, важно придерживаться некоторых правил. Складывая или вычитая числа, учитывают абсолютные отклонения. Если числа нужно разделить или перемножить, прибегают к относительным показателям

Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.

Если числа нужно разделить или перемножить, прибегают к относительным показателям. Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.

Результаты фиксируются в виде десятичных дробей. Точное значение может быть очень длинным, вплоть до бесконечного. Для удобства используют только среднее значение

При этом важно помнить о существовании верных и сомнительных цифр. У первой категории цифр разряд бывает выше допустимой погрешности, у второй — ниже.. При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%

Эта же закономерность применяется для оценки температуры и других физических величин.

При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%. Эта же закономерность применяется для оценки температуры и других физических величин.

4.4.4. Случайные погрешностей

Случайные составляющие основной погрешности средств измерений по ГОСТ 8.009 [] задаются своими среднеквадратическими отклонениями, поэтому их суммирование выполняется непосредственно по формуле геометрического суммирования (4.101).

Если случайная погрешность является коррелированным случайным процессом (см. п. ) и задана в виде функции автокорреляции или спектральной плотности мощности , то сначала находят среднеквадратическое значение случайной составляющей погрешности по формуле :

,

(4.107)

где — верхняя граничная частота полосы пропускания всего измерительного канала или цифрового фильтра, используемого при обработке полученных данных. Если задана функция автокорреляции, то спектральную плотность мощности находят по формуле (4.17).

Случайная составляющая погрешности может быть уменьшена в несколько раз (в зависимости от величины фликкер-шума) путем усреднения результатов многократных измерений (см. п. «Многократные измерения»).

Средняя квадратическая ошибка

_______Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:

где – сумма квадратов вероятнейших ошибок; n – число измерений. Средняя квадратическая ошибка арифметической середины вычисляется по формуле:

_______Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е. ε = 3 x m.

_______Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки.
___

_______Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины. Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая погрешность
измерения линии длиной:

_______l = 110 м, при m = 2 см, равна m/l = 1/5500.

_______Пример:

_______Линия измерена шесть раз. Определить ее вероятнейшую длину и оценить точность этого результата. Вычисления приведены в таблице:

Таб. 1

_______По формулам вычислены абсолютные средние квадратические ошибки, а оценивать
точность измерения длины линии необходимо по относительной ошибке. Поэтому нужно абсолютную ошибку разделить на длину линии. Для нашего примера относительная
ошибка вероятнейшего значения измеренной линии равна