Эффект холла и его применение

Свойства[ | код]

В простейшем рассмотрении эффект Холла выглядит следующим образом. Пусть через проводящий брусок в слабом магнитном поле с индукцией B{\displaystyle B} течёт электрический ток с плотностью j{\displaystyle j} под действием напряжённости E{\displaystyle E}. Магнитное поле будет отклонять носители заряда к одной из граней бруса от их движения вдоль или против электрического поля. При этом критерием малости будет служить условие, что при этом носители заряда не начнут двигаться по циклоиде.

Таким образом, сила Лоренца приведёт к накоплению отрицательного заряда возле одной грани бруска, и положительного — возле противоположной. Накопление заряда будет продолжаться до тех пор, пока возникшее электрическое поле зарядов E1{\displaystyle E_{1}} не скомпенсирует силу Лоренца:

eE1=evB⇒E1=vB.{\displaystyle eE_{1}=evB\Rightarrow E_{1}=vB.}

где e{\displaystyle e} — электрический заряд электрона.

Скорость электронов v{\displaystyle v} можно выразить через плотность тока j{\displaystyle j}:

j=nev⇒v=jne,{\displaystyle j=nev\Rightarrow v={\frac {j}{ne}},}

где n{\displaystyle n} — концентрация носителей заряда. Тогда

E1=1nejB.{\displaystyle E_{1}={\frac {1}{ne}}jB.}

Коэффициент RH=1ne{\displaystyle R_{H}={\frac {1}{ne}}} пропорциональности между E1{\displaystyle E_{1}} и jB{\displaystyle jB} называется коэффициентом (или константой) Холла. В таком приближении знак постоянной Холла зависит от знака носителей заряда, что позволяет определить знак их заряда для большого числа металлов и полупроводников.

Несмотря на то, что носителями заряда в металлах являются электроны, имеющие отрицательный заряд, для некоторых металлов — например, таких, как свинец, цинк, железо, кобальт, вольфрам в достаточно сильном магнитном поле наблюдается положительный знак константы Холла RH{\displaystyle R_{H}}, что объясняется в полуклассической и квантовой теориях твёрдого тела.

Какие бывают разновидности эффекта Холла

Данный эффект бывает трех видов:

• аномальный;
• квантовый;
• спиновой.

Аномальный эффект способен проявляться в ненамагниченных материалах. Т.е. это такой метод, при котором появление напряжения не обусловлено влиянием магнитного поля. При этом необходимым условием для наблюдения данного эффекта является нарушение инвариантности по отношению к обращению времени в системе.

Квантовый эффект Холла отличается тем, что он квантуется только в сильно намагниченных полях, которые приводят к кардинальной перестройке внутренней структуры двумерной электронной жидкости.

Спиновый эффект Холла наблюдается в ненамагниченных проводниках, которые не переместили в поле действия силовых линий магнита. Смыслом данного эффекта является то, что электроны с антипараллельными спинами отклоняются к противоположным краям пластины.

Эффект аудитории и теория вытеснения

Это то влияние, которое аудитория имеет на человека или на группу людей, выполняющих определенную задачу у всех на виду. Этот эффект был открыт в 30-х годах XX века. Он заключается в двух противоположных явлениях: результаты многих выступающих (атлетов в особенности) обычно оказываются выше, когда на них смотрит большое количество людей, в то время как у других присутствие зрителей вызывает чувство неловкости, поэтому они заканчивают свои выступления с худшим результатом, чем могут в действительности.

В 1965г. социальный психолог Роберт Зайонц обнаружил связь эффекта аудитории с так называемой теорией вытеснения. Зайонц доказал: будет ли влияние аудитории позитивным или негативным, зависит от относительной «легкости» выполняемой задачи. Если, например, выступающий верит, что победит, эффект аудитории будет подвигать его к выступлению на высшем уровне. Если он в себе не уверен, то наличие аудитории может привести к ещё большему снижению его самооценки.

Теория за принципом эффекта Холла

Прежде всего мы должны понять, что такое электрический ток. Электрический ток — это в основном поток заряженных частиц через проводящий путь. Эти заряженные частицы могут быть «отрицательно заряженными электронами» или даже «положительно заряженными отверстиями» (пустоты, в которых должны находиться электроны). Теперь давайте перейдем к теме.

Если мы возьмем тонкую проводящую пластину (как показано выше на рис. 1 и повторено ниже для простоты считывания) и подключим ее к цепи с батареей (источником напряжения), то ток начнет течь по ней. Носители заряда будут течь по прямой линии от одного конца пластины к другому.

Поскольку носители заряда находятся в движении, они будут создавать магнитное поле. Теперь, когда вы поместите магнит рядом с пластиной, его магнитное поле будет искажать магнитное поле носителей заряда. Это расстроит прямой поток носителей заряда. Сила, которая нарушает направление потока носителей заряда, называется силой Лоренца.

Из-за искажения в магнитном поле носителей заряда отрицательные заряженные электроны будут отклоняться на одну сторону пластины, а положительные заряженные дыры — на другую сторону. Вот почему разность потенциалов (также называемая напряжением Холла) будет генерироваться между обеими сторонами пластины, что можно измерить с помощью измерителя.

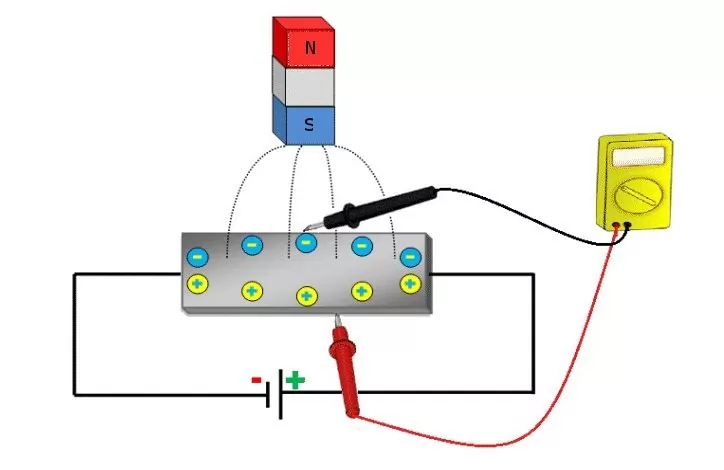
Этот эффект известен как эффект Холла. Чем сильнее магнитное поле, тем больше электронов будет отклоняться. Это означает, что чем выше ток, тем больше электронов будет отклоняться. И чем больше будут отклоняться электроны, тем больше будет разность потенциалов между обеими сторонами пластины. Поэтому мы можем сказать, что:

Устройство и примеры использования

Простейшая система с датчиком Холла включает в свой состав следующие элементы:

1. Постоянный магнит (его функция – создание магнитного поля).
2. Подвижный ротор с лопастями или зубцами.
3. Особый стержень из магнитного материала (магнитопровод).
4. Пластиковый корпус.

Помимо этого, техническая характеристика датчика предусматривает применение микросхем, задействованных в измерительном процессе.

Понять принцип работы этого прибора удается, если ознакомиться с подробной схемой включения датчика Холла в зоне проведения измерений. Схема подключения и суть работы сенсора может быть представлена следующим образом:

• В зазоре, образованном половинками магнитопровода, перемещаются металлические лопасти ротора.
• При их вращении происходит периодическое шунтирование магнитного потока.
• Встроенной микросхемой предусмотрено определение нулевого показателя индукции (в эти моменты напряжение на ее выходе максимально).
• По частоте таких всплесков, подсчитываемой той же микросхемой, судят о скорости вращения контролируемого объекта (двигательного вала в мотоцикле, например).

Чтобы этот процесс протекал нормально – при включении сенсора в измерительную цепь должна учитываться цоколевка данного образца (она бывает разной).

Обобщая рассмотренную схему, следует предположить, что датчики этого класса способны измерять скорость вращения коленвала любого движущегося средства. Универсальность сенсора, не исключающая возможности его установки в скутере, например, позволяет применять датчик Холла не только в сложных технических устройствах, но и в обычной бытовой технике.

Применение в системе зажигания и стиральных машинах

При использовании датчика Холла в системе зажигания автомобиля с его помощью удается фиксировать момент размыкания трамблера. В данном случае он работает как аналоговый преобразователь, определяющий мгновения прерывания бортового питания. На этом же принципе базируется его применение в рабочих модулях стиральной машины, что позволяет по скорости вращения барабана определять увеличение веса белья.

Датчики Холла устанавливаются и в некоторых образцах измерительной аппаратуры. Чаще всего ими комплектуются бесконтактные клещи, применяемые для измерения тока в проводниках. Встроенный прибор реагирует на изменение электромагнитного поля, образующегося вокруг силового кабеля. Кроме того, он подходит для ручки газа электровелосипеда, позволяя контролировать угол ее поворота.

В бытовых условиях

В клавиатурах компьютеров эти приборы обеспечивают бесконтактный способ снятия информации. Сенсор, входящий в состав кулера бытового ПК, способен управлять полярностью обмоток ротора, то есть менять направление его вращения.

При использовании такого элемента в смартфоне, в частности, он обеспечивает выключение устройства при помещении его в чехол с «магнитной» застежкой.

Рассматривая области применения датчики Холла простыми словами можно сказать, что его использование в технической сфере практически ничем не ограничено. В электронном конструкторе Ардуино, например, имеется набор с таким датчиком, позволяющий на практике проиллюстрировать эффект Холла.

Это не единственный пример его использования в целях обучения, помогающий начинающим пользователям понять, как подключить и использовать сенсоры полевых структур.

В заключение отметим, что к недостаткам датчиков Холла относят их чувствительность к электромагнитным помехам, нередко возникающим в рабочих цепях. Кроме того, использование сложных электронных модулей в конструкции прибора в какой-то мере влияет на его надежность, несколько снижая ее. Эти минусы сенсора не рассматриваются как его дефекты, а просто учитываются при работе с аппаратурой.

Теперь вы знаете, что такое датчик Холла, как он работает и зачем нужен. Надеемся, предоставленная информация была для полезной и интересной!

Материалы по теме:

• Что такое тензодатчик и как он устроен
• Для чего нужны концевые выключатели
• Чем отличается переменный ток от постоянного

Опубликовано:
09.07.2019
Обновлено: 09.07.2019

Эффект Холла и его применение

Эффект Холла был открыт уже более века назад, но особого внимания удостоился только в последние три-четыре десятилетия. Первое практическое применение (не считая лабораторных исследований) эффекта Холла было в 50-х годах в датчике микроволнового излучения.

Затем, в связи с освоением массового производства полупроводниковой продукции, эффект Холла стал применяться более широко. В 1968 году произошла революция в производстве микропереключателей: появилась первая твердотельная клавиатура.

Вначале чувствительный элемент и остальную электронику производили как отдельные узлы, но сейчас датчики на эффекте Холла используются практически везде: в компьютерах и швейных машинах, в автомобилях и самолетах, инструментах и медицинском оборудовании.

Эффект Холла технологически является очень выгодным. Чувствительный элемент — это всего лишь тонкая пластинка проводящего материала с выводами, расположенными перпендикулярно протеканию тока.

Если эту пластинку подвергнуть воздействию магнитного поля, то напряжение на выводах изменится пропорционально величине напряженности этого магнитного поля. Напряжение на выводах очень мало, порядка микровольт, и требуется дополнительное усиление, чтобы добиться напряжения, с которым можно работать.

Когда элемент Холла объединяется со вспомогательной электроникой — получается датчик Холла. Сердцем всех микропереключателей основанных на эффекте Холла является микросхема, состоящая из элемента Холла и согласующей схемы.

Несмотря на то, что датчик Холла чувствителен к магнитному полю, он может быть использован как основной элемент в различных типах датчиков, таких как датчики тока, температуры, давления, положения и т. д. Принцип его применения в следующем.

Датчик Холла всегда реагирует на изменение магнитного поля, созданного магнитной системой. В свою очередь состояние магнитной системы изменяется в зависимости от изменения измеряемой величины: температуры, давления, положения или какого-нибудь другого параметра через входной преобразователь.

Выходной преобразователь формирует необходимый выходной сигнал измерителя, используя напряжение датчика Холла.

Основные преимущества использования датчика Холла следующие:

• монолитность конструкции;
• высокая наработка на отказ (порядка 30 миллиардов операций);
• высокая скорость срабатывания (частота переключений свыше 100 кГц);
• способность работы при не подвижной магнитной системе;
• отсутствие подвижных частей;
• совместимые логические уровни входов и выходов;
• допустимые рабочие температуры от -40 до +150 °C;
• высокая точность повторяемости операций.

Магнитные датчики

Основное преимущество использования датчиков магнитного поля, заключается в их бесконтактной работе. Они бывают аналоговыми и дискретными. Первый тип считается классическим. В его основе лежит принцип, что чем сильнее будет магнитное поле, тем больше будет величина напряжения. В современных приборах и устройствах такой тип уже практически не используется из-за значительных размеров. Цифровой же датчик построен на режиме работы «ключ» и имеет два устойчивых положения. Если сила индукции недостаточна он не срабатывает.

Разделяются дискретные элементы Холла на два типа:

• униполярные — срабатывание которых зависит от полюса магнитного поля;
• биполярные — переключения состояния датчика происходит при изменении магнитного полюса;
• омниполярные — реагируют на действие магнитной индукции любого направления.

Конструктивно датчик представляет собой электронный прибор с тремя выводами. Он может выпускаться как в стандартном исполнении DIP, DFN или SOT, так и в герметичном: например, 1GT101DC (герметичный), A1391SEHLT-T (DNF6), SS39ET (SOT), 2SS52M (DIP).

https://youtube.com/watch?v=y5sjX8qpJbY

Характеристики устройства

Выпускаемые датчики, использующие явление Холла, как и любые электронные радиокомпоненты характеризуются своими параметрами. Главным из них является тип прибора и напряжение питания. Но, кроме этого, выделяют следующие технические характеристики:

1. Величина измеряемой индукции. Измеряется она в гауссах или миллитеслах.
2. Чувствительность — определяется значением магнитного потока, на который реагирует датчик, единица измерения мВ/Гс или мВ/мТл.
3. Нулевое напряжение магнитного поля — значение разности потенциалов, соответствующее отсутствию магнитного поля.
4. Дрейф нуля — изменение напряжения, зависящее от температуры. Указывается в процентном отклонении от температуры 25 °C.
5. Дрейф чувствительности — изменение чувствительности, вызванное изменением температуры.
6. Полоса пропускания — уровень снижения чувствительности с шагом в 3 дБ.
7. Индукция включения и выключения — это значение напряжённости поля, при котором датчик устойчиво срабатывает.
8. Гистерезис — разность между индукциями включения и выключения;
9. Время срабатывания — характеризуется промежутком времени перехода из одного устойчивого состояния в другое.

Изготовление приборов

Материал, из которого выполняется элемент Холла, должен обладать большой подвижностью носителей зарядов. Для получения наибольшего значения напряжения вещество не должно иметь высокую электропроводностью. Поэтому при производстве устройств используется: селенид, теллурид ртути, антимонид индия. Тонкопленочные датчики получаются методом испарения вещества и осаждения его на подложку. В качестве её служит слюда или керамика.

Изготавливают датчики также из полупроводников — германия и кремния. Их легируют мышьяком или фосфорной сурьмой. Такие устройства обладают низкой зависимостью от изменения температуры, а величина образуемой на них ЭДС может достигать одного вольта.

Типовой процесс производства пластинчатого датчика Холла состоит из следующих операций:

• обрезка пластины нужного размера;
• шлифовка поверхности;
• формирование с помощью пайки либо сварки симметричных выводов;
• герметизация.

Одним из главных преимуществ датчиков, выполненных на этом эффекте, является электрическая изоляция (гальваническая развязка) делающие их применение удобным и безопасным.

Квантовый эффект Холла

Впервые необычный (англ. unconventional) квантовый эффект Холла наблюдали в работах, где было показано, что носители в графене действительно обладают нулевой эффективной массой, поскольку положения плато на зависимости недиагональной компоненты тензора проводимости соответствовали полуцелым значениям холловской проводимости ν=±(|n|+12){\displaystyle \nu =\pm (|n|+1/2)} в единицах 4e2h{\displaystyle 4e^{2}/h} (множитель 4 появляется из-за четырёхкратного вырождения энергии), то есть

σxy=±4e2h(|n|+12){\displaystyle \sigma _{xy}=\pm {\frac {4e^{2}}{h}}\left(|n|+{\frac {1}{2}}\right)}.

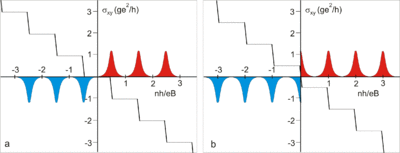
Это квантование согласуется с теорией квантового эффекта Холла для дираковских безмассовых фермионов. Сравнение целочисленного квантового эффекта Холла в обычной двумерной системе и графене смотрите на рисунке 1. Здесь показаны уширенные уровни Ландау для электронов (выделение красным цветом) и для дырок (синий цвет). Если уровень Ферми находится между уровнями Ландау, то на зависимости холловской проводимости σxy{\displaystyle \sigma _{xy}} наблюдается ряд плато. Эта зависимость отличается от обычных двумерных систем (аналогом может служить двумерный электронный газ в кремнии, который является двухдолинным полупроводником в плоскостях эквивалентных {100}, то есть тоже обладает четырёхкратным вырождением уровней Ландау и холловские плато наблюдаются при ν=4|n|{\displaystyle \nu =4|n|}).

Квантовый эффект Холла (КЭХ) может использоваться как эталон сопротивления, потому что численное значение наблюдаемого в графене плато равное h2e2{\displaystyle h/2e^{2}} выполняется с хорошей точностью, хотя качество образцов уступает высокоподвижному ДЭГ в GaAs, и, соответственно, точности квантования. Преимущество КЭХ в графене в том, что он наблюдается при комнатной температуре (в магнитных полях свыше 20 Т). Основное ограничение на наблюдение КЭХ при комнатной температуре накладывает не само размытие распределения Ферми-Дирака, а рассеяние носителей на примесях, что приводит к уширению уровней Ландау.

p-n переход

Из-за отсутствия запрещённой зоны в графене в структурах с верхним затвором можно сформировать непрерывный p-n переход, когда напряжение на верхнем затворе позволяет инвертировать знак носителей, задаваемый обратным затвором в графене, где концентрация носителей никогда не обращается в ноль (кроме точки электронейтральности) и нет области лишённой носителей как в обычных p-n переходах. В таких структурах тоже можно наблюдать квантовый эффект Холла, но из-за неоднородности знака носителей значения холловских плато отличаются он приведённых выше. Для структуры с одним p-n переходом значения квантования холловской проводимости описываются формулой

G=2e2h|ν′||ν||ν′|+|ν|,{\displaystyle G={\frac {2e^{2}}{h}}{\frac {|\nu ^{‘}||\nu |}{|\nu ^{‘}|+|\nu |}},}

где ν{\displaystyle \nu } и ν′{\displaystyle \nu ^{‘}} — факторы заполнения в n- и p- области соответственно (p-область находится под верхним затвором), которые могут принимать значения ±2,±6,±10{\displaystyle \pm 2,\pm 6,\pm 10} и т. д. Тогда плато в структурах с одним p-n переходом наблюдаются при значениях 1, 3/2, 3, 5/3 и т. д. Такие значения плато были наблюдены в эксперименте.

p-n-p переход

Для структуры с двумя p-n переходами соответствующие значения холловской проводимости равны

G=e2h|ν′||ν|2|ν′|+|ν|=23,65,67,…(νν′).{\displaystyle G={\frac {e^{2}}{h}}{\frac {|\nu ^{‘}||\nu |}{2|\nu ^{‘}|+|\nu |}}={\frac {2}{3}},{\frac {6}{5}},{\frac {6}{7}},…(\nu \nu ^{‘}

Расщепление основного уровня Ландау

В работе наблюдается спиновое расщепление релятивистских уровней Ландау и снятие четырёхкратного вырождения для наинизшего уровня Ландау вблизи точки электронейтральности. Для объяснения этого эффекта предложено несколько теорий.

Виды

Цифровые датчики Холла делятся на униполярные и биполярные

Помимо эффекта Холла, законы которого описаны классической физикой и соблюдаются во всех нормальных или приближённых к нормальным условиям экспериментах, выделяют ещё несколько разновидностей явления возникновения разности потенциалов в проводнике.

Аномальный

Аномальным называют любой случай накопления заряда на грани проводника, в котором исключено воздействие внешних магнитных полей. Необходимым условием является перпендикулярная направленность разницы потенциалов относительно направления силы тока.

Квантовый

Законы возникновения разницы потенциалов в «квантовом мире» исследуются на примере плоского проводника типа ДЭГ (двумерный электронный газ). Квантовый наблюдается в сильных магнитных полях и при низких температурах. Он выражается в квантовании холловского сопротивления, которое на графике имеет чётко выраженные «участки плато». Чем выше сопротивление, тем длиннее участки плато и выше разница между ними.

Дробный

Многие передовые учёные в 80-х годах прошлого века заинтересовались исследованиями фон Клитцинга и продолжили изучать свойства разности потенциалов в ДЭГ. Наибольших успехов достигли Даниэль Цуи и Хорст Штёрмер, которые проанализировали промежуточные участки между «плато сопротивления» и пришли к выводу, что при существенном увеличении интенсивности магнитных полей «участки плато» можно получить и на дробных значениях электронных уровней Ландау, например, при n=1/3; n=2/5; n=3/7 и т. д.

Такое явление получило название дробного квантового эффекта Холла, а его первооткрыватели получили Нобелевскую премию по физике в 1998 году. В настоящее время ведутся расширенные исследования квантового и дробного квантового видов данного эффекта.

Спиновый

В 2003–2004 годах было изучено поведение электронов с антипараллельными спинами в проводниках, изолированных от каких-либо магнитных полей. Теоретической базой исследования послужили теории Владимира Переля, выдвинутые в далёком 1971 году. Они были доказаны на практике, когда удалось зафиксировать отклонения данных групп электронов к противоположным граням проводника. Движение заряженных частиц напоминает первый вид эффекта — аномальный.

Формулы и расчёты

Закон полного тока

Так как в классическом определении эффект Холла – это перемещение зарядов под воздействием внешнего магнитного поля, можно сделать несколько выводов:

• образующееся в контрольных точках напряжение (Uх) будет прямо пропорционально току (I);
• аналогичная зависимость определена силовыми параметрами поля, которые выражают через вектор (В) магнитной индукции;
• существенное значение имеет размерность проводника.

Какой получится потенциал при определенных исходных параметрах? Ниже показан алгоритм преобразований с итоговой формулой для расчетов.

Для определения силы Лоренца (Fл) используют выражение:

Fл = q*v*B,

где:

• q – элементарный заряд;
• v – скорость его перемещения.

При подключении пластины по схеме основного эксперимента при постоянной силе тока разница потенциалов стабилизируется. После этого созданное электрическое поле будет воздействовать на заряды с определенной силой Fэ = q * E, где E – это соответствующая напряженность.

В этом состоянии Fл = Fэ, поэтому значение правых частей формул также будет равным: q*v*B = q * E. Следовательно E = v*B.

Плотность тока (j) определяется выражением:

j = q * v *n, где n – это число заряженных частиц в единице объема.

После преобразования выражения расчет для скорости подставляют в формулу напряженности:

E = (j/q*n) * B.

Разницу потенциалов несложно вычислить по напряженности и расстоянию (d) между контрольными точками (гранями пластины):

Uх = E * d = d * (j/q*n) * B = (1/q*n) * d * j * B.

Часть выражения (1/q*n) = R – это постоянная Холла. Она определяет обратную зависимость от суммарного заряда частиц.

Подставив коэффициент Холла в последнее выражение, можно записать итоговую формулу следующим образом:

Uх = R * d * j * B.

Вывод

Используемые размеры
Б.→{\ displaystyle {\ vec {B}}}	Плотность магнитного потока
Э.→{\ displaystyle {\ vec {E}}}	Напряженность электрического поля
Ф.→{\ displaystyle {\ vec {F}}}	Усилие на грузовом носителе
UЧАС{\ Displaystyle U _ {\ mathrm {H}}}	Напряжение Холла
Я.{\ displaystyle I}	Электрический ток
j→{\ displaystyle {\ vec {j}}}	Плотность электрического тока
v→{\ displaystyle {\ vec {v}}}	Скорость дрейфа носителей заряда
б{\ displaystyle b}	Ширина проводника
d{\ displaystyle d}	Толщина проводника
п{\ displaystyle n}	Плотность носителя
q{\ displaystyle q}	Загрузка грузового автомобиля
А.ЧАС{\ Displaystyle А _ {\ mathrm {H}}}	Постоянная холла

Базовые знания векторного исчисления и электродинамики помогут понять этот раздел .

Здесь следует сделать краткий вывод формулы для напряжения Холла. Срок действия вывода ограничен электрическими проводниками только с одним типом носителя заряда, такими как металлы (электроны) или сильно легированные полупроводники (преимущественно дырки или электроны).

Движущиеся носители заряда в магнитном поле испытывают силу Лоренца :

Ф.→знак равноq(v→×Б.→){\ Displaystyle {\ vec {F}} = д \, ({\ vec {v}} \ раз {\ vec {B}})}

Эффект Холла создает компенсирующее электрическое поле , которое нейтрализует отклоняющее действие магнитного поля. Следовательно, к результирующей силе, действующей на несущие элементы, должно применяться следующее:

q(Э.→+v→×Б.→)знак равно{\ displaystyle q \, ({\ vec {E}} + {\ vec {v}} \ times {\ vec {B}}) = 0}

Для простоты система координат настроена таким образом, что носители заряда движутся в одном направлении, а магнитное поле действует в этом направлении. Так оно и есть . Таким образом, y-составляющая приведенного выше уравнения становится после деления на :
Икс{\ displaystyle x}z{\ displaystyle z}v→знак равно(vИкс,,){\ displaystyle {\ vec {v}} = (v_ {x}, 0,0)}Б.→знак равно(,,Б.z){\ displaystyle {\ vec {B}} = (0,0, B_ {z})}q{\ displaystyle q}

Э.у-vИксБ.zзнак равно{\ displaystyle \ left.E_ {y} -v_ {x} B_ {z} = 0 \ right. \,}

Плотность тока в проводнике обычно можно выразить как Если вы нарушите эту связь и поместите ее в приведенное выше уравнение , вы получите
j→{\ displaystyle {\ vec {j}}}j→знак равнопqv→{\ displaystyle {\ vec {j}} = nq {\ vec {v}}}vИкс{\ displaystyle v_ {x}}

Э.узнак равно1пqjИксБ.zзнак равноА.ЧАСjИксБ.z{\ displaystyle E_ {y} = {\ frac {1} {nq}} \, j_ {x} B_ {z} = A _ {\ mathrm {H}} \, j_ {x} B_ {z}}

Это соотношение определяет постоянную Холла , которая характеризует силу эффекта Холла.
А.ЧАС{\ Displaystyle А _ {\ mathrm {H}}}

Чтобы сделать уравнение более управляемым, проводник, в котором произошло разделение зарядов , можно рассматривать как пластинчатый конденсатор. Для этого применяется отношение

Э.узнак равноUЧАСб{\ displaystyle E_ {y} = {\ frac {U _ {\ mathrm {H}}} {b}}}.

Кроме того, плотность тока в данном случае может быть выражена как. Если вы воспользуетесь этими двумя обозначениями, вы получите выражение для напряжения Холла, которое зависит только от легко измеряемых величин :
jИкс{\ displaystyle j_ {x}}jИксзнак равноЯ.бd{\ displaystyle j_ {x} = {\ frac {I} {bd}}}UЧАС{\ Displaystyle U _ {\ mathrm {H}}}

UЧАСзнак равноА.ЧАСЯ.Б.zd{\ Displaystyle U _ {\ mathrm {H}} = A _ {\ mathrm {H}} \, {\ frac {IB_ {z}} {d}}}.

Это уравнение также верно для проводников с разными типами носителей заряда, но тогда постоянная Холла больше не может быть вычислена. Так называемое сопротивление Холла можно определить из уравнения :
А.ЧАСзнак равно1пq{\ Displaystyle А _ {\ mathrm {H}} = {\ гидроразрыва {1} {nq}}}

Р.(Б.)знак равноА.ЧАСБ.zd{\ Displaystyle R (B) = A _ {\ mathrm {H}} \, {\ frac {B_ {z}} {d}}}

Сопротивление Холла характеризует элемент Холла , но не имеет ничего общего с электрическим сопротивлением, измеренным на элементе Холла . Он указывает отношение напряжения Холла к току элемента Холла при определенной плотности магнитного потока:

Р.(Б.)знак равноUЧАСЯ.{\ Displaystyle R (B) = {\ гидроразрыва {U _ {\ text {H}}} {I}}}