Деформация кручения

Измерения

1. Прежде всего установите диапазон амплитуд, в котором выполняется условие (8). Для этого укрепите грузы на некотором расстоянии от проволоки и возбудите в системе крутильные колебания. Измеряя время нескольких (не менее 10-ти) полных колебаний, найдите период Т1

   . уменьшая амплитуду вдвое, тем же способом найдите соответствующий периодТ2 . еслиТ1= Т2 , то для проведения измерений можно выбрать любую амплитуду не больше первой. Если же окажется, что , то амплитуду необходимо уменьшить до такого значения , начиная с которого для всех < будет справедливо равенствоТ1= Т2 .

2. Проверьте справедливость неравенства (7).
3. Установив грузы так, чтобы их центры масс находились на некотором расстоянии L1

   от оси системы, измерьте период, как описано выше. ЕслиJ – момент инерции без грузов, аJ1 – момент инерции грузов, то, очевидно:

. (9)

Изменив расстояние грузов до величины L2

, аналогично получим:

. (10)

Из (9) и (10) следует:

,

где 2т

– масса двух грузов. Масса одного груза 550 г.

Определение величины ƒ

проведите для нескольких (не менее 5-ти) пар значенийL1 иL2 . величинуƒ можно также найти из наклона прямой в графике, по осям которого отложеныL2 иТ2 . разработка этого вопроса предоставляется читателю.

1. Зная ƒ

   , найдите значение модуля сдвигаG по формуле (2) и оцените допущенную при этом погрешность.

Построение эпюры касательных напряжений

Касательные напряжения по высоте круглого сечения, будут распределены следующим образом:

Как видишь, касательные напряжения будут максимальны на поверхности стержня, они нас и будут интересовать больше всего, т. к. по ним выполняются прочностные расчёты, для них и будем строить эпюру – максимальных касательных напряжений.

Расчёт максимальных касательных напряжений

Максимальные касательные напряжения в поперечном сечении, можно определить по формуле:

где Wp — полярный момент сопротивлния, T — крутящий момент.

Полярный момент сопротивления для круглого сечения определяется по формуле:

Поэтому формулу для нахождения максимальных касательных напряжений для круглого поперечного сечения, можно записать в следующем виде:

По условию задачи . Осталось вычислить максимальные касательные напряжения на каждом участке:

По полученным значениям построим эпюру касательных напряжений:

Задача на температурные напряжения при кручении

Стальные стержни 1 и 2 нагреваются на

А.

Определить максимальные напряжения.

При нагреве стержней на

температурные напряжения.

Напряжения, вызванные изменением температуры в стержне постоянного сечения, не зависят от его длины, площади поперечного сечения, а зависят от модуля упругости, коэффициента линейного расширения

разности температур

Эти напряжения создадут усилия:

Тогда крутящий момент:

Касательные напряжения:

Следует помнить, что при нагреве стержней в них возникают сжимающие напряжения, а при охлаждении – растягивающие. Эти напряжения, суммируясь с напряжениями от силовых факторов, могут значительно превышать допускаемые. Это обстоятельство следует учитывать при проектировании элементов конструкций.

Пример решения задачи на кручение стержня круглого сечения

Кручение стержня круглого сечения – условие задачи

К стальному валу постоянного поперечного сечения (рис. 3.8) приложены четыре внешних скручивающих момента: кН·м; кН·м; кН·м; кН·м. Длины участков стержня: м; м, м, м. Требуется: построить эпюру крутящих моментов, определить диаметр вала при кН/см2 и построить эпюру углов закручивания поперечных сечений стержня.

Определяем реактивный момент, возникающий в жесткой заделке

Обозначим момент в заделке и направим его, например, против хода часовой стрелки (при взгляде навстречу оси z).

Запишем уравнение равновесия вала. При этом будем пользоваться следующим правилом знаков: внешние скручивающие моменты (активные моменты, а также реактивный момент в заделке), вращающие вал против хода часовой стрелки (при взгляде на него навстречу оси z), считаем положительными.

Тогда

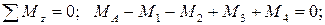
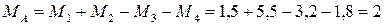кН·м.

Знак «плюс» в полученном нами выражении говорит о том, что мы угадали направление реактивного момента , возникающего в заделке.

Строим эпюру крутящих моментов

Напомним, что внутренний крутящий момент , возникающий в некотором поперечном сечении стержня, равен алгебраической сумме внешних скручивающих моментов, приложенных к любой из рассматриваемых частей стержня (то есть действующих левее или правее сделанного сечения). При этом внешний скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки (при взгляде на поперечное сечение), входит в эту алгебраическую сумму со знаком «плюс», а по ходу – со знаком «минус».

Соответственно, положительный внутренний крутящий момент, противодействующий внешним скручивающим моментам, направлен по ходу часовой стрелки (при взгляде на поперечное сечение), а отрицательный – против ее хода.

Разбиваем длину стержня на четыре участка (рис. 3.8, а). Границами участков являются те сечения, в которых приложены внешние моменты.

Делаем по одному сечению в произвольном месте каждого из четырех участков стержня.

Cечение 1 – 1. Мысленно отбросим (или закроем листком бумаги) левую часть стержня. Чтобы уравновесить скручивающий момент кН·м, в поперечном сечении стержня должен возникнуть равный ему и противоположно направленный крутящий момент . С учетом упомянутого выше правила знаков

кН·м.

Сечения 2 – 2 и 3 – 3:

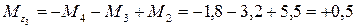кН·м;

кН·м.

Сечение 4 – 4. Чтобы определить крутящий момент, в сечении 4 – 4 отбросим правую часть стержня. Тогда

кН·м.

Легко убедиться в том, что полученный результат не изменится, если мы отбросим теперь не правую, а левую часть стержня. Получим

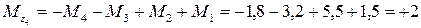кН·м.

Для построения эпюры крутящих моментов проводим тонкой линией ось, параллельную оси стержня z (рис. 3.8, б). Вычисленные значения крутящих моментов в выбранном масштабе и с учетом их знака откладываем от этой оси. В пределах каждого из участков стержня крутящий момент постоянен, поэтому мы как бы «заштриховываем» вертикальными линиями соответствующий участок. Напомним, что каждый отрезок «штриховки» (ордината эпюры) дает в принятом масштабе значение крутящего момента в соответствующем поперечном сечении стержня. Полученную эпюру обводим жирной линией.

Отметим, что в местах приложения внешних скручивающих моментов на эпюре мы получили скачкообразное изменение внутреннего крутящего момента на величину соответствующего внешнего момента.

Определяем диаметр вала из условия прочности

Условие прочности при кручении имеет вид

,

где – полярный момент сопротивления (момент сопротивления при кручении).

Наибольший по абсолютному значению крутящий момент возникает на втором участке вала: кН·см.

Тогда требуемый диаметр вала определяется по формуле

см.

Округляя полученное значение до стандартного, принимаем диаметр вала равным мм.

Что означает понятие крутящий момент детально

Многие ли из нас понимают в мощности автомобилей и что означают лошадиные силы? Никогда не приходила мысль сравнить автомобиль мощностью 100 л.с. с повозкой со ста скакунами, и что как-то странно сравнивать движок в 1,6 литра с сотней лошадей, которые и танк с места сдвинут а не только малолитражную машину?

Это ошибочное сравнение и вот почему.

Итак, давайте разберемся что есть мощность двигателя. В научном определении под мощностью понимается скорость преобразования и передачи энергии. Для двигателя это работа, которую он проделывает за единицу времени. Мощность двигателя измеряется в Ваттах, хотя нам более привычно измерять в лошадиных силах.

Единицу измерения в одну лошадиную силу получили опытным путем и определяется она как способность лошади поднять 75 кг на один метр в секунду, т.е. лошадиная сила равняется 735 Ваттам. Вместо переносимого веса используют крутящий момент, который равен силе, возникающей на определенном радиусе.

Крутящий момент — это механическая энергия от воспламеняющейся смеси в цилиндре, которая передается на коленчатый вал, трансмиссию, раздаточную передачу, колеса, и толкает, заставляя автомобиль двигаться. Обороты двигателя оказывают самое прямое влияние на крутящий момент.

Для примера возьмем мотор от Форд Фокуса объемом 1,6 л., который развивает мощность 100 л.с. и обладает крутящим моментом 150 Н*м.

Если учесть, что в килограмме десять ньютон, и если приделать к валу двигателя прут длиной 1 метр, то для того, чтобы не дать двигателю вращаться, достаточно повесить на этот прут всего 15 кг. 150 Н*м — это максимальный крутящий момент который развивается при оборотах двигателя близким к 4000 оборотам в минуту.

Так почему же двигатель, который можно удержать одной рукой, имеет характеристики 100 л.с.? Все это потому, что мощность зависит не только от силы, развиваемой на валу двигателя, но и от скорости вращения этого вала. Чем больше оборотов способен развивать двигатель, тем он мощнее.

С увеличением рабочего объема возрастает сила, которая действует на поршень и на крутящий момент. Также, чем сильнее давление в камере сгорания цилиндра, тем сила, давящая на поршень, больше. Чем больше площадь поршня тем меньше сила и удельное давление.

К примеру, 2-х литровых двигатель СкайЭктив от Мазды, развивающий 150 л.с., будет существенно шустрее разгонять автомобиль, чем 2-х литровый бензиновый двигатель Киа или Хёндэ и не только потому, что первый развивает больше крутящий момент, а потому, что он развивается раньше и полка крутящего момента у него шире за счёт большей компрессии в цилиндрах.

Высокий крутящий момент помогает автомобилю быстрее ускориться на разгоне при небольших оборотах коленвала, улучшаются тяговые свойства силового механизма, например, грузоподъемность машины и ее проходимость.

Максимальный показатель крутящего момента достигается мотором при конкретных оборотах. Бензиновые моторы имеют более высокое значение, нежели дизельные двигатели.

Наибольший крутящий момент у четырех цилиндрованного бензинового мотора достигается при 4000 оборотах (примерно 192 н*м), у турбированного 4х цилиндрового при 4500 оборотах (265 н*м), а у дизельного 4-х цилиндрового движка — при 2750 оборотах (400 н*м).

Какой двигатель лучше исходя из крутящего момента? Это спорный вопрос — все зависит от назначения. Если вы ездите на микроавтобусе либо занимаетесь грузоперевозками, то для вас важна тяга с нижних оборотов — тогда подойдет дизель с его низко оборотистым двигателем и высоким крутящим моментом (т.е. он тянуть будет просто бешено). Когда необходима высокая скорость — вы любите раскручивать двигатель до 6000-6500 оборотов в минуту, то здесь необходим бензин.

Автоконцерны придумывают разные способы чтобы увеличить крутящий момент, используя турбонаддув, управляемых фаз газораспределения, увеличения степени сжатия, благодаря конструктивных инновациям ДВС и т.д.

Рычаг

В каждом дворе есть качели, для которых нужны два качающихся (если в вашем дворе таких нет, посмотрите в соседнем). Большая доска ставится посередине на точку опоры. По сути своей, качели — это рычаг.

Рычаг — простейший механизм, представляющий собой балку, вращающуюся вокруг точки опоры.

Хорошо, теперь давайте найдем плечо этой конструкции. Возьмем правую часть качелей. На качели действует сила тяжести правого качающегося, проведем перпендикуляр от линии действия силы до точки опоры. Получилась, что плечо совпадает с рычагом, разве что рычаг — это вся конструкция, а плечо — половина.

Давайте попробуем опустить качели справа, тогда что получим: рычаг остался тем же самым по длине, но вот сместился на некоторый угол, а вот плечо осталось на том же месте. Если направление действия силы не меняется, как и точка опоры, то перпендикуляр между ними невозможно изменить.

Правило равновесия рычага Рычаг находится в равновесии тогда, когда силы, действующие на него, обратно пропорциональны плечам этих сил. F1, F2 — силы, действующие на рычаг l1, l2 — плечи этих сил

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов mi, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений: т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов mi, расположенных по одну сторону от рассматриваемого сечения.

Правило знаков внутренних скручивающих моментов: Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

В технике наиболее широко используются валы круглого поперечного сечения.

Теория кручения круглых валов основана на следующих гипотезах:

1. поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
2. радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.

Сдвиг

Сдвигом называют такую деформацию твердого тела, при которой все его плоские слои, параллельные некоторой плоскости сдвига, не искривляясь и не изменяясь в размерах, смещаются параллельно друг другу (рис. 3).

Рис. 3.

Деформация сдвига возникает под действием сил, приложенных к двум противоположным граням тела так, как показано на рисунках 3; 4. Эти силы вызывают смещение слоев тела, параллельных направлению сил. Расстояние между слоями не изменяется. Любой прямоугольный параллелепипед, мысленно выделенный в теле, превращается в наклонный.

Рис. 4.

Мерой деформации сдвига является угол сдвига γ — угол наклона вертикальных граней (рис. 5).

Рис. 5.

Сдвиг происходит под действием касательной силы F, приложенной к грани ВС, параллельной плоскости сдвига. Грань АД, параллельная ВС, закреплена неподвижно.

Так как угол мал, формулу можно записать в виде:

где СС1 = D X — абсолютный сдвиг, γ — угол сдвига, называемый также относительным сдвигом, выражается в радианах.

По закону Гука относительный сдвиг γ пропорционален касательному напряжению τ = F/S, где S — площадь поверхности грани ВС, т.е.

τ = F / S = Gg

где G — модуль сдвига.

Закон Гука для малой деформации сдвига выражается формулой:

Коэффициент G, зависящий от материала тела, называется модулем сдвига и характеризует упругие свойства тела при деформации сдвига. Например, для стального образца G = 76 ГПа.

Модуль сдвига равен касательному напряжению, которое возникло бы в образце при относительном сдвиге, равном 1 (при условии, что закон Гука выполняется).

Деформацию сдвига испытывают, например, заклепки и болты, соединяющие металлические конструкции. Сдвиг при больших углах приводит к разрушению тела — срезу. Срез происходит при работе ножниц, пилы и др.

Обратите внимание на принципиальное отличие модуля кручения от модуля сдвига, который зависит только от материала. Модуль кручения зависит не только от материала, но ещё и от диаметра и от длины цилиндра

Дата добавления: 2015-04-01; 8147; Опубликованный материал нарушает авторские права? | Защита персональных данных |

Не нашли то, что искали? Воспользуйтесь поиском:

Это интересно: Деформация изгиба — определение, формула, примеры

Определение изгибающих и крутящих моментов

скручивающих элементов машины работают на совместное действие кручения и изгиба. Эти детали имеют коленчатый вал. При расчете элементов, действующих одновременно на изгиб и кручение, сначала необходимо изучить расчетные значения изгибающих моментов

круглого сечения со шкивом и кривошипом. Схема вала показана на рисунке. 443 и 444. Рассмотрим момент, когда натяжение ремня T и t на правом конце кривошипного пальца становится горизонтальной силой P, а кривошип становится вертикальным. Размеры конструкции можно найти на чертежах. Объявления, которые определяют изгиб и крутящий момент вала. Сила,

действующая на шкив T и t (натяжение ремня), заменяется силой T4-L, приложенной в центре колеса, а пара (T-t)R Q Ro является радиусом шкива. Сила Т4~Т, вместе с весом шкива к, произведет гнуть вала; РО пары (т—т), переплетая вал, сбалансировано парой приложенной к правому концу. Заменить силу Р, действующую на палец кривошипа, силой Р, приложенной к валу при продолжении оси точки М и парой моментов Р/G0. Таким образом, pH§и (T—t)

R o приложены к концам вала; при равновесии, равномерном ходе машины, моменты этих пар равны и момент скручивания. Если мощность, передаваемая валом со скоростью вращения p и шкивом N в единицу времени, известна, то величина крутящего момента§ 166] определения изгиба и крутящего момента 511. Можно найти по формуле (11.3)§ 56: L4C= 716,2 Вт Тогда R= ХК И Т= 7?О (1-м)’ Где W=u. Что касается изгиба, то на вал действуют как вертикальные (Q), так

и горизонтальные (P) силы. Поэтому мы строим моменты appspy для каждого из них(рис. 445, а и в), считая подшипники В и с, опоры вала шарнирно сочленены; один из них имеет продольную подвижность. Имея график момента от вертикальной и горизонтальной нагрузок, мы показываем суммарный изгиб Mo 446 как геометрическую сумму обеих составляющих каждой секции вала, изображающую вектор-подобный геометрический изгибающий момент для секции\, где суммирующий момент равен Ma=V = V = V = V = V = V = V.

не влияя на результаты расчета, и мы изгибаем МО для всех сечений это делается на рисунке. 445, B. заметим, что график всего изгибающего момента L4I между участками B и C ограничен максимальной кривой, не давая доказательства Из контура графика видно, что опасной деталью может быть либо подшипник в, либо подшипник с, в зависимости от соотношения числовых данных.

Примеры решения задач по сопромату

Внецентренное сжатие или растяжение.	Определение напряжений и проверка прочности при изгибе с кручением
Ядро сечения	Вычисление напряжений и деформаций.

Расчеты стержней при кручении

Нагружение стержня, при котором из всех внутренних силовых факторов в его поперечных сечениях не равен нулю только момент, вектор которого направлен вдоль оси стержня, называется кручением. Стержни, работающие в таких условиях, называются валами.

При кручении цилиндрического вала, в его поперечных сечениях возникают только касательные напряжения, и это напряженное состояние называется «чистый сдвиг». При этом, поперечные сечения вала остаются плоскими и не меняют своего размера в радиальном направлении. Так же не меняются расстояния между поперечными сечениями, но при этом они поворачиваются друг относительно друга на некоторый угол φ.

В общем случае, максимальные касательные напряжения возникают у края поперечного сечения, за исключением наружных углов, в которых касательные напряжения равны нулю. Стержень не круглого поперечного сечения испытывает депланации — точки его сечения выходят из плоскости и перемещаются вдоль оси стержня в различных направлениях.

Онлайн расчеты, представленные в данном разделе, рассматривают кручение круглого вала сплошного сечения, кручение круглого вала с отверстием, выполненным с эксцентриситетом, треугольное, прямоугольное сечение, а так же кручение стержней стандартных сечений — уголка, двутавра и швеллера.

Основные понятия и зависимости.

Под кручением

стержня понимается такой вид нагружения, при котором в его поперечных сечениях возникает только крутящий моментМкр , а в поперечных сечениях возникают только касательные напряжения τ. (Прочие силовые факторы, т.е. Nz, Qx, Qy, Mx, My– равны нулю ).

Валом называется

– стержень, работающий на кручение. При расчете стержня (вала) на кручение требуется решить две основные задачи: прочность и жесткость. Если система является статически неопределимой, то необходимо раскрыть статическую неопределимость.

Для крутящего момента, независимо от формы сечения, принято следующее правило знаков. Если наблюдатель смотрит на поперечное сечение со стороны внешней нормали и видит момент Мкр

направленным против часовой стрелки, то момент считается положительным.

Расчет момента силы

Сейчас рассмотрим несколько вариантов того, как момент может рассчитываться. По идее просто нужно умножить силу на плечо, но поскольку мы имеем дело с векторами, все не так просто.

Если сила расположена перпендикулярно оси стержня, мы просто умножаем модуль силы на плечо.

Расстояние между точками A и B — 3 метра.

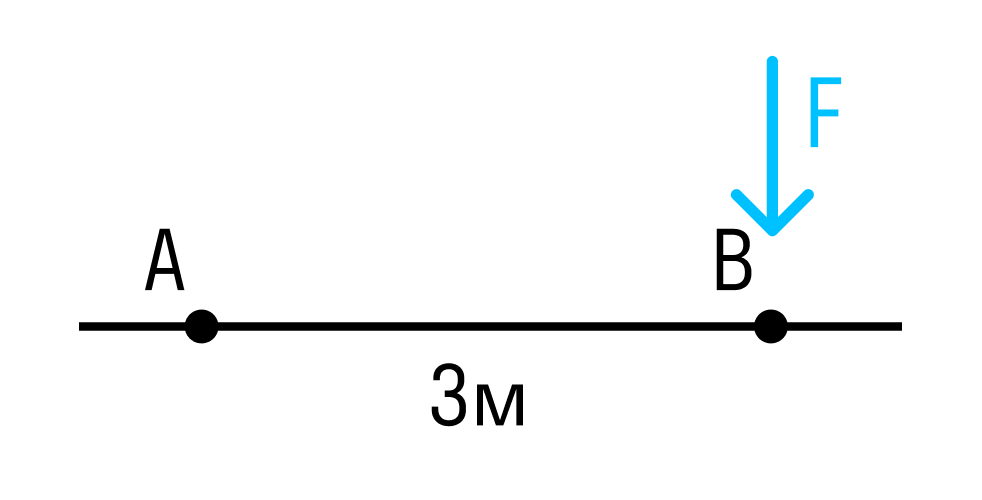
Момент силы относительно точки A:

           МА=F×AB=F×3м

Если сила расположена под углом к оси стержня, умножаем проекцию силы на плечо.

Обратите внимание, что такие задания могут встретиться только у учеников не раньше 9 класса!

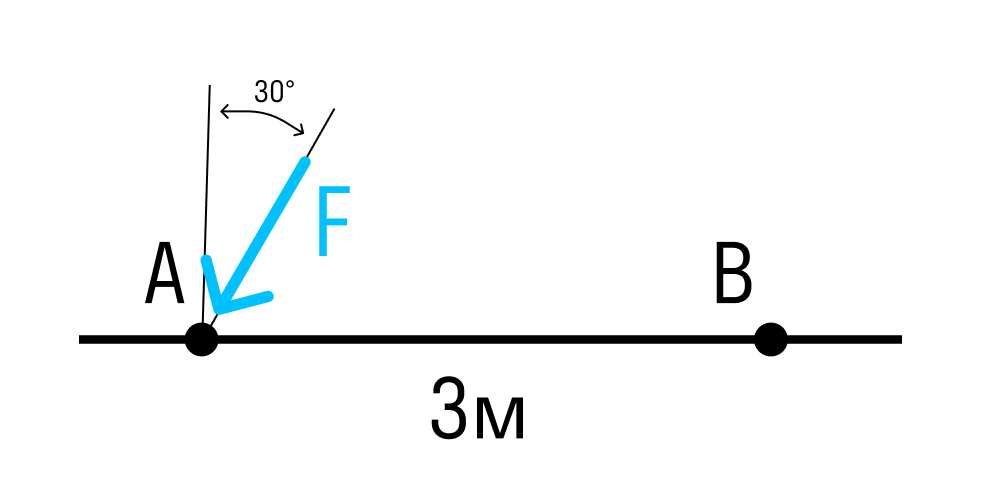
Момент силы относительно точки B:

           MB=F×cos30×AB=F×cos30×3м

Если известно самое короткое расстояние от точки до линии действия силы, момент рассчитывается как произведение силы на это расстояние (плечо).

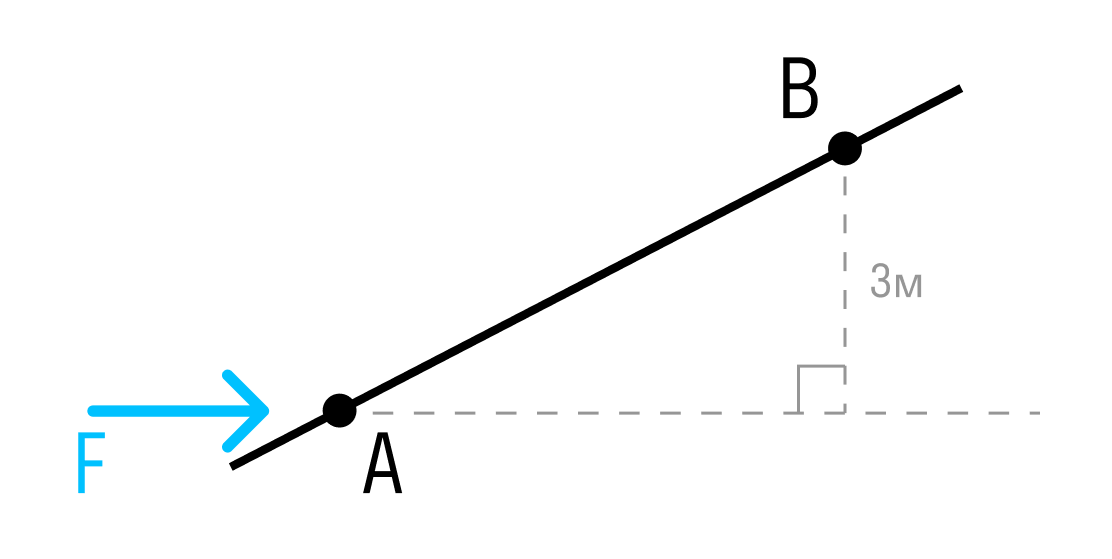
Момент силы относительно точки B:

           MB=F×3м

Общие сведения

В момент силы можно понимать как «вращающая сила». В единицей измерения момента силы является (Н·м). Момент силы иногда называют моментом пары сил, это понятие возникло в трудах над рычагами. В простейшем случае, если сила приложена к рычагу перпендикулярно ему, момент силы определяется как произведение величины этой силы на расстояние до оси вращения рычага. Например, сила в 3 ньютона, приложенная к рычагу на расстоянии 2 метра от его оси вращения, создаёт такой же момент, что и сила в 1 ньютон, приложенная к рычагу на расстоянии 6 метров от оси вращения. Более точно момент силы частицы определяется как :

M→=r→×F→,{\displaystyle {\vec {M}}=\left,}

где F→{\displaystyle {\vec {F}}} — сила, действующая на частицу, а r→{\displaystyle {\vec {r}}} — частицы (в предположении, что ось вращения проходит через начало координат).

Что такое момент силы

Определение

Моментом силы считается векторная величина в физической науке, которая равняется векторному произведению радиус-вектора, приведенного от оси вращения к точке приложения силы и ее направления.

Категория характеризует воздействие силы по отношению к твердому телу.

Случается, что велосипедисту приходится раскручивать колесо транспорта рукой. Рука берется за покрышку, т.к. таким способом колесо приводится в действие намного быстрее, чем при хватании велосипеда за спицы, поскольку они расположены ближе к точке оси вращения. Приводимое действие и будет считаться моментом силы, т.е. вращающимся.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут

Примечание

Вращающийся и крутящийся моменты не являются идентичными понятиями, поскольку «вращающийся» момент означает внешнее усилие, приложенное к объекту, в то время как «крутящийся» выражается во внутреннем усилии, возникающем в объекте под воздействием нагрузок.

Физическая наука трактует момент силы как вращение.

Единица измерения — ньютон-метр. В теории данную категорию также называют моментом пары сил — этот термин восходит к трудам Архимеда над рычагами. Так, если усилие прикладывается к рычагу перпендикулярно, то момент силы выступает как умножение величины приложенного усилия на расстояние до оси вращения рычага.

В механике линейного движения сила выступает мерой возможности для придания линейного ускорения телу. Аналогично, момент силы точки является мерой возможности сообщения углового ускорения системы. Он также выступает причиной возникновения углового ускорения — две этих категории прямо пропорциональны друг другу.

Пример

Так, если мы толкнем дверь дальше от дверных петель, т.е. там, где находится ручка, она откроется легче и быстрее. Отсюда видна разная возможность совершения вращения/поворота. Другой пример. Тяжелый предмет легче удерживается, если прижимать к нему руку вплотную, а не держать ее вытянутой. Таким образом, в указанных случаях момент силы меняется при уменьшении/увеличении рычага воздействия.

Формула моментов выглядит так:

\(dL\;=\;M\ast dt\)

М — момент силы (также обозначается как т), а dL — изменение момента импульса за бесконечно малый промежуток времени dt.

Так что же важнее и лучше

Здесь сложно сказать одно выходит из другого. С одной стороны момент, позволит развивать вам быстро максимальную мощность, в примере с дизелем, но он не сможет крутиться до таких оборотов как бензин, а значит его максимальная мощность в пике будет ниже. Тут знаете, кому что нужно, может быть вы водитель коммерческого транспорта, и вам не нужна максимальная скорость но важна тяга «с низов». Или наоборот, вы любите турбо моторы, которые крутятся до 8000 – 9000 оборотов и выстреливают с места.

Лично мне нравятся новые бензиновые агрегаты, такие как скажем у МАЗДЫ, мотор Skyactiv  которые сейчас устанавливаются на многие модели. Здесь увеличили степень сжатия, немного приблизили мотор к дизелю, но он остался бензиновым с высокими оборотами. Здесь есть и мощность и крутящий момент, золотая середина! Думаю за такими моторами будущее (если не брать гибриды и электромобили).

И запомните: — крутящий момент толкает машину вперед, а вот мощность это то, что этот момент производит. Так что покупаем лошадиные силы, а ездим на моменте!

Сейчас видео версия статьи, смотрим.

А сейчас голосование, что вы считаете важнее – крутящий момент или мощность двигателя.

НА этом заканчиваю, читайте наш АВТОБЛОГ, подписывайтесь на канал в YOUTUBE.

Кручение бруса прямоугольного сечения

Опыт показывает, что при кручении брусьев некруглого поперечного сечения сами сечения не остаются плоскими, то есть происходит депланация поперечных сечений. Исследовать напряженное и деформированное состояние таких брусьев при кручении методами сопротивления материалов не представляется возможным, так как в основе их лежит гипотеза плоских сечений (гипотеза Бернулли).

Задача о кручении бруса некруглого, в частности, прямоугольного сечения решена с помощью метода теории упругости, и на основе этого решения предложены простые расчетные формулы, имеющие ту же структуру, что и формулы для бруса круглого сечения, а именно:

Здесь: W_к=α∙h∙b 2 – момент сопротивления при кручении,

В этих формулах: b – меньшая из сторон прямоугольника,

h – большая сторона,

α, β – коэффициенты, значения которых приводятся в таблице в зависимости от отношения сторон h/b (эта таблица содержится в рубрике «Кручение», «Таблицы» или в любом учебнике сопротивления материалов).

Распределение касательных напряжений по прямоугольному сечению тоже отличается от распределения в круглом сечении:

Значения коэффициента γ Запись опубликована 05.09.2014 автором admin в рубрике Задачи, Задачи на кручение.

Источник

Внутренний крутящий момент

Внутренние скручивающие моменты появляются под действием внешних крутящих моментов mi, расположенных в плоскостях, перпендикулярных к продольной оси бруса.

Скручивающие моменты передаются на вал в местах посадки зубчатых колес, шкивов ременных передач и т.п.

Величина крутящего момента в любом сечении вала определяется методом сечений: т.е. крутящий момент численно равен алгебраической сумме скручивающих моментов mi, расположенных по одну сторону от рассматриваемого сечения.

Правило знаков внутренних скручивающих моментов: Положительными принимаются внутренние моменты, стремящиеся повернуть рассматриваемую часть вала против хода часовой стрелки, при рассмотрении со стороны отброшенной части вала.

В технике наиболее широко используются валы круглого поперечного сечения.

Теория кручения круглых валов основана на следующих гипотезах:

1. поперечное сечение, плоское до деформации вала, остается плоским и после деформации;
2. радиусы, проведенные мысленно в любом поперечном сечении, в процессе деформации вала не искривляются.