Передаточное отношение. передаточное отношение зубчатой передачи

Передаточное отношение цепной передачи

В подобной ременной передаче ремень может быть заменен на цепь, в этом случае шкивы также должны быть заменены на звездочки. Полученная передача называется цепной, она знакома каждому, ведь именно такая применяется на велосипедах. Для нее передаточное отношение определяется так же, как для ременной, но можно воспользоваться и соотношением количества зубьев на звездочках (ведущей и ведомой). Однако при таком расчёте передаточное отношение будет обратным, то есть передаточное число определяется делением числа зубьев ведомой звездочки на число зубьев ведущей (z2/z1).

Отличительной особенностью цепной передачи является повышенный уровень шума, а также износ при работе на высоких скоростях, поэтому ее при необходимости использования лучше всего ставить после уменьшения оборотов. В автомобиле возможно применение цепной передачи для привода ГРМ, правда, ограничением такого применения является повышенный уровень шума при ее работе.

Что такое передаточное число катушки

Давайте для начала разберемся, что такое передаточное число катушки, каким оно бывает и как это число может повлиять на вашу рыбалку.

В современных механизмах крутящий момент в различных узлах обеспечивается за счет зубчатой передачи. Это когда между собой сцеплены две шестерни, одна из которых передает движение другой. Таким образом, одна из них является ведущей (ее крутит двигатель или рыбак через ручку), а вторая ведомая, поскольку ее движение обеспечивается первой. Частота вращения обеих шестерен может в корне отличаться. Таким образом, каждая шестеренка может осуществлять свое количество оборотов за одинаковый отрезок времени. Связано это с разным количеством зубьев, от которых и зависит скорость вращения.

Рассмотрим небольшой пример. Если ведущая шестерня будет содержать 60 зубьев, а ведомая — только тридцать, то пока первая сделает один оборот, вторая прокрутится целых два раза. Чтобы узнать передаточное число такой катушки, значение зубьев ведущей шестерни делят на аналогичное число для ведомой, то есть 60/3=2. Таким образом, передаточное число в нашем примере равняется двум. Итак, зная значение этой характеристики катушки, о каких ее свойствах мы можем узнать предварительно?

Прежде всего, отметим, что внутренний механизм катушки состоит из множества шестерен. Они могут быть различными по своим свойствам. Как только рыбак начинает крутить рукоятку, он запускает движение ведущей шестерни с заданным количеством зубьев, а она уже приводит в работу остальные механизмы.

Интересно отметить, что при помощи передаточного числа возможно регулировать крутящий момент катушки. Это достигается путем изменения количества зубьев в передаче.

Итак, полученное вращение главная шестерня передает на одну или несколько следующих, которые находятся с ней в зацеплении. Последняя из этих шестерен (или ведомая) вращает ротор лесоукладывателя. Производителем рассчитано строгое количество оборотов, которое она будет совершать за одно полное движение рукоятки катушки. Чтобы узнать передаточное число катушки, необходимо соотнести между собою количество вращений ротора с оборотами ручки.

Сближенный и растянутый ряд в коробке передач

Не менее важным фактором, определяющим характер автомобиля, является разрыв между передаточными числами. Сближенный ряд передач гарантирует максимальное ускорение, которого может достичь автомобиль при прочих равных условиях. Кроме того, если во главу угла ставится экономичность, то такое решение позволяет держать рабочие обороты в оптимальной зоне, что также способствует продлению ресурса мотора.

Однако, есть у короткого ряда и существенный недостаток, а именно – необходимость в растянутой 1-й передаче, либо в короткой – высшей. Последствия от этого вполне очевидны, а единственным разумным решением является увеличение числа передач, что делает конструкцию дорогостоящей. Либо, всё же — переход к растянутому ряду.

Выбор решения обычно продиктован типом создаваемого автомобиля. Для скоростной и динамичной модели применяют сближенные по величине передаточного отношения передачи. Если же под капотом установлен двигатель с широким диапазоном мощности и плавным графиком крутящего момента, например – дизель, то необходимость в сближении передач отпадает. Для примера рассмотрим автомобиль Формулы-1, которые имеют очень плотный передаточный ряд, ввиду чего величина передаточных отношений 7-й и 8-й передач отличается всего в 1,12 раза, против 1,25 – у гражданских моделей.

Однако, сближенный ряд не всегда означает более высокую производительность. Например, у спортивного велосипеда, как правило, 8 очень близких по передаточному числу ступеней, при этом шестерня первой из них имеет 30 зубцов, а высшей – 11, это позволяет обеспечить наиболее рациональное использование энергии велосипедиста. Однако при таком подходе для обеспечения максимального ускорения необходимо интенсивно переключаться в интервале с 1-й по 5-ю передачу, всего за несколько секунд. Это касается и автомобилей, поскольку необходимость в столь частом переключении, как правило, предопределяет работу двигателя в неоптимальном режиме, особенно у неопытного водителя.

Всех этих недостатков лишены так называемые бесступенчатые типы трансмиссий, которые позволяют плавно изменять передаточные отношения, в зависимости от выбранного режима езды. К таким конструкциям относят, прежде всего, вариаторы, однако на сегодняшний день механизма, способного передавать огромный крутящий момент и оперативно подстраиваться под разгонную динамику спортивных моделей, пока не создано. Но прогресс не стоит на месте и непрерывная работа по совершенствованию таких агрегатов уже сделала их широко распространённым решением.

Определение передаточных отношений простейших планетарных и дифференциальных передач

Планетарными называются передачи, в которых оси одного или нескольких колес закреплены в подвижном звене – водиле.

Любая планетарная передача состоит из трех групп элементов. Первая группа – центральные колеса (колеса, расположенные на неподвижных осях), вторая группа – сателлиты (колеса, расположенные на подвижном звене – водиле) и третья группа – водила.

На рис. 237 показана схема передачи, состоящей из центрального колеса 1, сателлита 2 и водила H.

В общем случае центральное колесо и водило могут получать вращение от двух источников независимо друг от друга. Такая передача имеет две степени свободы и называется дифференциальной.

Если закрепить центральное колесо, то получается передача с одной степенью свободы – движение можно передавать либо от водила к сателлиту, либо от сателлита к водилу – такая передача называется простой планетарной (рис. 238).

Чтобы в процессе решения задач глубже проанализировать кинематику планетарных передач, целесообразно не пользоваться готовыми выведенными в учебниках формулами, а применять метод сложения двух движений.

Сателлиты планетарных передач совершают сложное вращательное движение. Движение сателлитов относительно Земли (относительно неподвижной системы координат) складывается из вращения их вместе с водилом – переносного движения и вращения их вокруг осей, закрепленных в водиле, – относительного движения.

Метод сложения двух движений можно распространить и на центральные колеса. Так, например, закрепленное центральное колесо простой планетарной передачи можно считать вращающимся вместе с водилом и одновременно поворачивающимся на их общей оси в обратную сторону с такой же скоростью, что и водило.

Поэтому метод, который подробно изложен в решениях задач, включает следующие четыре этапа:

1. Мысленно закрепляем все колеса на водиле и придаем ему вращение с угловой скоростью водила относительно его собственной неподвижной оси – получаем первое движение.

2. Освобождаем колеса от водила. Водило мысленно закрепляем (превращаем планетарную передачу в обычную зубчатую передачу с неподвижными осями) и поворачиваем центральное колесо с угловой скоростью -(n_H-n_ц), т. е. с угловой скоростью, равной разности абсолютных скоростей водила и центрального колеса, но в обратную сторону относительно направления вращения водила. В результате этого движения центрального колеса все остальные колеса передачи получают соответствующие угловые скорости, определяемые при помощи передаточных отношений. Так получается второе движение.

3. Угловые скорости всех элементов передачи, получившиеся в первом и втором движениях, складываем.

4. Из получившихся в результате сложения действительных зависимостей между угловыми скоростями определяем неизвестные в задаче величины.

Введем такие обозначения:

n₁, n₂, n₃, … (или ω₁, ω₂, ω₃, …) – угловые скорости, выраженные в об/мин (рад/сек) у зубчатых колес (центральных или сателлитов), дифференциальных передач, индексы соответствуют нумерации колес; n_H (или ω_H) – угловая скорость водила в дифференциальной передаче.

Угловые скорости колес или водила в простой планетарной передаче (с закрепленным колесом) обозначим теми же буквами, но с верхними индексами в скобках, соответствующих закрепленному колесу, например n₂(1) (или ω₂(1)) – угловая скорость второго колеса при закрепленном первом; n_H(1) – угловая скорость водила при закрепленном первом и т. д.

Аналогично обозначим и передаточные отношения:

i₁₂(H) – передаточное отношение от колеса 1 к колесу 2 при неподвижном водиле;

i_2H(1) – передаточное отношение от колеса 2 к водилу при неподвижном первом колесе;

i_1H – передаточное отношение от колеса 1 к водилу в дифференциальной передаче и т. д.

При решении задач с планетарными передачами необходимо очень внимательно следить за правильностью определения знаков передаточных отношений между отдельными элементами передачи. Правило знаков передаточных отношений приведено в § 39.

Задача 201. Определить передаточное отношение от сателлита 2 к водилу H для простой планетарной передачи, показанной на рис. 238, если числа зубьев…

Задача 202. Определить передаточное отношение от колеса 2 к водилу H простой планетарной передачи с закрепленным колесом внутреннего зацепления (рис. 239),…

Задача 204. Определить передаточное отношение i_H1(3) для простой планетарной передачи, показанной на рис. 241, если числа зубьев…

Задача 205. Определить угловую скорость водила H и колеса 2 дифференциального зубчатого механизма (рис. 242), если число зубьев колес z₁=18,…

Многоступенчатая передача

Для увеличения кинематического эффекта несколько зубчатых пар могут последовательно соединяться в единый . Такой механизм называется многоступенчатым зубчатым механизмом или многоступенчатой передачей
. Схема одного из таких механизмов приведена на рисунке 36.

Рисунок 36

Запишем передаточные отношения для каждой пары колес данного механизма:

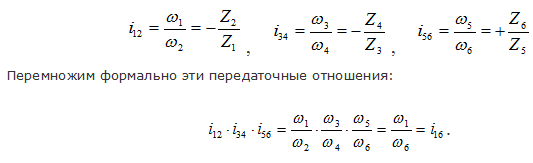
Из схемы видно, что колеса 2 и 3 находятся на одном валу и вращаются с одной угловой скоростью (ω 2 = ω 3
), аналогично ω 4 = ω 5
. Поэтому в приведенном выше уравнении эти члены сократились.

Таким образом, общее передаточное отношение многоступенчатого механизма равно произведению частных передаточных отношений ступеней, из которых состоит данный механизм:

В этой формуле “m” – число передач внешнего зацепления (если число передач внешнего зацепления четное, то знак «+», т.е. колеса на входе и на выходе вращаются в одну сторону; если нечетное, то знак «–». Количество передач внутреннего зацепления не учитывается, т.к. внутреннее зацепление не изменяет направление вращения).

В приведенном примере m=2 (пары Z 1* Z 2 и Z 3* Z 4 ; пара Z 5* Z 6 – пара внутреннего зацепления) и, таким образом, колеса «1» и «6» вращаются в одну сторону.

О главной паре

Практически все виды передач используются в автомобиле – крутящий момент от двигателя проходит цепочку различных устройств и претерпевает изменения, начиная от КПП, главной пары, и заканчивая колесами автомобиля. Все передаточные отношения для КПП и главной пары влияют непосредственным образом на динамику автомобиля. Поэтому с целью

1. уменьшения частоты переключения;
2. возможности движения при спокойной езде на небольших оборотах двигателя;
3. повышения верхнего порога скорости движения,

передаточные отношения, в том числе и для главной пары, должны быть уменьшены. Для улучшения разгонной динамики все должно быть наоборот.

Работа различных механизмов и устройств, в том числе и в автомобиле, не может происходить без преобразования используемой энергии, как по величине, так и по направлению. Оценить и рассчитать величину необходимого изменения, а также его последствия, помогает передаточное отношение.

Что еще стоит почитать

Виды коробок передач Турбонаддув двигателя

Виды парктроников

Ремень газораспределительного механизма

Редуктор заднего моста

Купить мотор-редуктор

ПТЦ «Привод» – производитель редукторов и мотор-редукторов с разными характеристиками и КПД, которому не безразличны показатели окупаемости его оборудования. Мы постоянно работаем не только над повышением качества нашей продукции, но и над созданием самых комфортных условий ее приобретения для вас.

Специально для минимизации ошибок выбора нашим клиентам предлагается интеллектуальный конфигуратор. Чтобы воспользоваться этим сервисом, не нужны специальные навыки или знания. Инструмент работает в режиме онлайн и поможет вам определиться с оптимальным типом оборудования. Мы же предложим лучшую цену мотор-редуктора любого типа и полное сопровождение его доставки.

Оценка статьи:

Сохранить себе в:

Как рассчитать редуктор на понижение оборотовСсылка на основную публикацию

Похожие публикации

• Как настроить нутромер индикаторный

Зависимость оборотов от диаметра шкива

как правильно рассчитать диаметры шкивов, чтобы ножевой вал деревообрабатывающего станка вращался со скоростью 3000…3500 оборотов в минуту. Частота вращения электрического двигателя 1410 оборотов в минуту (двигатель трехфазный, но будет включен в однофазную сеть (220 В) с помощью системы конденсаторов. Ремень клиновой.

Диаметр шкива, в зависимости от частоты вращения вала и линейной скорости шкива, определяют по формуле:

где D1 — диаметр шкива, мм; V — линейная скорость шкива, м/с; n — частота вращения вала, об/мин.

Легко подсчитать, что для шкива на валу электродвигателя с частотой вращения 1400 об/мин, минимальный диаметр шкива (повышающая передача) при линейной скорости ремня 10 м/с составит около 136 мм.

Диаметр ведомого шкива вычисляют по следующей формуле:

D2 = D1x(1 — ε)/(n1/n2),

где D1 и D2 — диаметры ведущего и ведомого шкивов, мм; ε — коэффициент скольжения ремня, равный 0,007…0,02; n1 и n2 — частота вращения ведущего и ведомого валов, об/мин.

Так как значение коэффициента скольжения весьма мало, то поправку на скольжение можно и не учитывать, то есть вышестоящая формула приобретет более простой вид:

Минимальное расстояние между осями шкивов (минимальное межцентровое расстояние) составляет:

где Lmin — минимальное межцентровое расстояние, мм; D1 и D2 — диаметры шкивов, мм; h — высота профиля ремня.

Чем меньше межцентровое расстояние, тем сильнее изгибается ремень при работе и тем меньше срок его службы. Целесообразно принимать межцентровое расстояние больше минимального значения Lmin, причем делают его тем больше, чем ближе значение передаточного отношения к единице. Но во избежание чрезмерной вибрации применять очень длинные ремни не следует. Кстати, максимальное межцентровое расстояние Lmax легко вычислить по формуле:

Lmax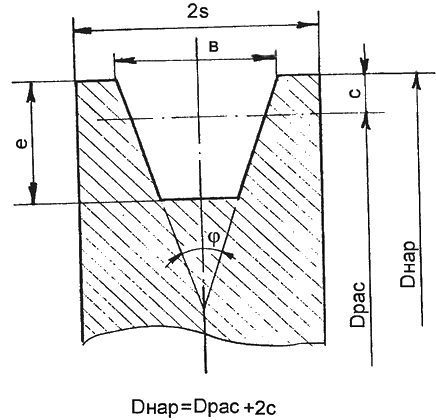

Работы по переборке электродвигателя подходят к завершению. Приступаем к расчёту шкивов ремённой передачи станка. Немного терминологии по ремённой передаче.

Главными исходными данными у нас будут три значения. Первое значение это скорость вращения ротора (вала) электродвигателя 2790 оборотов в секунду. Второе и третье это скорости, которые необходимо получить на вторичном валу. Нас интересует два номинала 1800 и 3500 оборотов в минуту. Следовательно, будем делать шкив двухступенчатый.

Заметка! Для пуска трёхфазного электродвигателя мы будем использовать частотный преобразователь поэтому расчётные скорости вращения будут достоверными. В случае если пуск двигателя осуществляется при помощи конденсаторов, то значения скорости вращения ротора будут отличаться от номинального в меньшую сторону. И на этом этапе есть возможность свести погрешность к минимуму, внеся поправки. Но для этого придётся запустить двигатель, воспользоваться тахометром и замерить текущую скорость вращения вала.

Наши цели определены, переходим выбору типа ремня и к основному расчёту. Для каждого из выпускаемых ремней, не зависимо от типа (клиноременный, поликлиновидный или другой) есть ряд ключевых характеристик. Которые определяют рациональность применения в той или иной конструкции. Идеальным вариантом для большинства проектов будет использование поликлиновидного ремня. Название поликлиновидный получил за счет своей конфигурации, она типа длинных замкнутых борозд, расположенных по всей длине. Названия ремня происходит от греческого слова «поли», что означает множество. Эти борозды ещё называют по другому – рёбра или ручьи. Количество их может быть от трёх до двадцати.

Поликлиновидный ремень перед клиноременным имеет массу достоинств, таких как:

• благодаря хорошей гибкости возможна работа на малоразмерных шкивах. В зависимости от ремня минимальный диаметр может начинаться от десяти – двенадцати миллиметров;
• высокая тяговая способность ремня, следовательно рабочая скорость может достигать до 60 метров в секунду, против 20, максимум 35 метров в секунду у клиноременного;
• сила сцепления поликлинового ремня с плоским шкивом при угле обхвата свыше 133° приблизительно равна силе сцепления со шкивом с канавками, а с увеличением угла обхвата сила сцепления становится выше. Поэтому для приводов с передаточным отношением свыше трёх и углом обхвата малого шкива от 120° до 150° можно применять плоский (без канавок) больший шкив;
• благодаря легкому весу ремня уровни вибрации намного меньше.

Принимая во внимание все достоинства поликлиновидных ремней, мы будем использовать именно этот тип в наших конструкциях. Ниже приведена таблица пяти основных сечений самых распространённых поликлиновидных ремней (PH, PJ, PK, PL, PM)

Виды приводных ремней

Видов ремней достаточно много, так как используются они в разных условиях. Где-то нужно передать очень большую мощность так, чтобы ремень не порвался и не растянулся. Где-то ремень не должен проскальзывать. Где-то ремень должен крутиться очень-очень быстро и мало изнашиваться со временем. А где-то нужно передать вращение на большое расстояние и под углом.

Очень распространенная классификация ремней – по поперечному сечению или форме. Основные виды: 1 — плоские ремни, 2 – клиновые ремни, 3 – ремни круглого сечения (пассики), 4 – многоручьевые ремни (или поликлиновые), 5 – зубчатые ремни.

Рис. 12. Виды приводных ремней

В крупной промышленной технике самые распространенные ремни – клиновые и поликлиновые. Они достаточно толстые по сечению и имеют увеличенную за счет боковой поверхности площадь сцепления со шкивами.

В небольших электронных устройствах чаще используются плоские ремни и пассики (ремни с круглым сечением).

Рис. 13. Четыре прядильные машины приводятся в движение от плоских приводных ремней с линейного вала. Лейпциг , Германия, около 1925 года

Плоские ремни широко использовались в 19-м и начале 20 века на фабриках для передачи движения на несколько машин с одного линейного вала (англ. line shaft). Они широко применялись и применяются в лесопильных станках, молотилках, электрогенераторах.

В станках с ЧПУ (3D-принтерах, плоттерах, лазерных станках) используются зубчатые ремни, так-так они сохраняют постоянное передаточное отношение и не проскальзывают.

Влияние передаточного числа на динамику

Передаточное число – величина вычисляемая, она находится отношением числа зубьев ведомой шестерни к количеству ведущей. Чем выше это значение, тем двигатель быстрее накрутит нужное количество оборотов и разгонит автомобиль более стремительно. «Супер!», — скажете вы, но ошибетесь в главном – максимум скорости в этом случае будет меньшим, а переключать передачи вам придется намного чаще. Поэтому производители придерживаются средних значений передаточных чисел КПП, создавая многоступенчатые конструкции.

Сначала конструкции КПП содержали 3 вала, где 3-я передача являлась прямой и позволяла достигать предельной скорости. Последующая же регулировка скорости сводилась к уменьшению оборотов двигателя через подачу топлива, в этом случае эффект управления скоростью достигался, но терялась экономичность авто совершенно. Поэтому количество передач увеличили, и бывшая прямая третья стала четвертой или пятой, а далее достигла и более высоких ступней.

Передаточные числа механической коробки передач самой распространенной 5-скоростной КПП находятся в следующих диапазонах:

• 1-я передача – от 3 до 4;
• 2-я передача – от 2 до 2,9;
• 3-я передача – от 1,2 до 1,9;
• 4-я передача – от 0,9 до 1,2;
• 5-я передача – от 0,7 до 0,9;
• задний ход – от 3 до 4.

Если передаточные числа АКПП будут настроены неправильно, то комфорта от поездки за рулем добиться не удастся. А вот в АКПП передаточные числа при несбалансированности способны равномерное движение автомобиля превратить в езду на упрямом осле, сопровождающуюся постоянными рывками и необоснованно большим расходом топлива.

Оптимальными специалисты считают значения, расположенные близко друг к другу, тогда у автомобиля будет разгон без рывков при переключении скоростей. Такого дробления не удастся осуществить, если передач будет мало, поэтому чем больше передач – тем лучше для вашего комфорта при вождении. Особенно это касается машин с автоматом: если есть возможность выбора, то АКПП с 5-ю, 6-ю, 7-ю скоростями будет намного предпочтительнее 4АКПП. Здесь за вас скорости переключает автоматика, и чем чаще она будет это делать, тем быстрее выйдут из строя дорогостоящие механизмы.

Часто значения передаточных чисел указывают в характеристиках автомобиля. За этими цифрами стоит скрупулезный подбор производителем оптимальных значений. Каких-то идеальных величин, как при оценке других параметров, здесь не существует. Поэтому назвать одно значение плохим, а другое хорошим нельзя, так как коробки передач влияют на динамику машины, а тип вождения и предпочтения у владельцев авто зачастую кардинально различны, и сложно рассматривать КПП отдельно от всего «организма» машины. Все скоростные режимы и рекомендации завода-изготовителя формируются только после определения передаточных чисел, ибо они должны учитывать такие нюансы, как:

• комфорт в управлении автомобилем, исключающий частое переключение передач как на механике, так и на автомате;
• хорошие показатели динамики автомобиля;
• все передачи должны работать слаженно, чтобы ни один режим поездки не выбивался из заданного ритма;
• расход топлива должен быть нормальным и соизмерим заявленной литражности, перегазовок быть не должно;
• длинная последняя передача способна разогнать авто до максимальной скорости;
• должна быть полная совместимость двигателя и передаточных чисел.

Последний пункт поясним немного подробнее. Для каждого двигателя разработчики создают коробку с заданными передаточными числами, поэтому задумываясь о замене КПП, вариант неродной коробки даже не стоит рассматривать. С данной модификацией вы можете приобрести массу проблем. Если новая коробка взята от такого же двигателя, но более мощного, то вам гарантирован больший износ мотора и не слишком удобное переключение скоростей, но к этому со временем можно привыкнуть, а вот преждевременный износ двигателя – вещь малоприятная.

Не лучше ситуация получается и при обратной замене – коробку взяли из пары, где двигатель был слабее. Этой модификацией вы обделите себя по потенциалу машины и увеличите топливные затраты на поездку.

Таким образом, для полноценной работы автомобиля в нем должна располагаться родная трансмиссия. Но народные умельцы автомобильного тюнинга уже научились менять в машине передаточное число, используя новые шестерни в рядах и получая другие характеристики модели. Такие модификации часто проводят с автомобилями ВАЗ. Следствие этого — более интенсивный разгон автомобиля, но приходится жертвовать максимальной скоростью.

Передаточное число гоночных автомобилей также разительно отличается от серийных моделей, ибо перед ними стоят другие задачи эксплуатации.

Выбор — передаточное число

Выбор передаточных чисел основной и дополнительной коробок передач производится при тяговом расчете автомобиля.
 

Выбор передаточного числа зависит от требуемой скорости движения автомобиля и мощности двигателя. У легковых автомобилей передаточное число колеблется в пределах от 3 2: 1 до 6 2: 1, у грузовых автомобилей — от 5 2: 1 до 7 5: I, а иногда и выше.
 

При выборе передаточного числа следует избегать общих множителей между числом ходов червяка и числом зубьев червячного колеса. В этом случае с помощью цилиндрической фрезы получают более чистую боковую поверхность и более высокую точность в положении начальной окружности червячного колеса, а также более благоприятные условия для работы и меньшего износа червячной передачи.
 

Вопрос о выборе передаточного числа мультипликатора представляет собой отдельную задачу.
 

Некоторые рекомендации по выбору передаточных чисел помещены в табл. 6.4. Наибольшие значения передаточных чисел следует принимать лишь в крайних случаях, так как передачи с наибольшими значениями i имеют большие габариты.
 

Может быть несколько причин, вызывающих желательность выбора передаточного числа у нижнего предела допустимых значений. Например, если нагрузка от трения составляет небольшую часть от общей нагрузки, то зубчатая передача может быть сделана более простой и экономичной.
 

К этим значениям и следует стремиться путем выбора передаточного числа кинематической схемы соединения электромагнита с исполнительным устройством при заданной противодействующей характеристике последнего и заданных размерах полюсного наконечника.
 

Вторым шагом при предварительном выборе основных параметров электропривода является выбор передаточного числа / редуктора, связывающего основной вал проектируемого механизма с двигателем.
 

Приведенные оптимальные передаточные числа являются лишь отправными величинами при выборе рабочего передаточного числа. Последнее выбирается после производства ряда расчетов с различными передаточными числами и сопоставления результатов с учетом максимально допустимой скорости механизма и требуемой мощности двигателя.
 

Если для привода используется высокоскоростной двигатель, то возникает проблема выбора передаточного числа механизма, связывающего двигатель с исполнительным звеном.
 

Таким образом, отмечая возможность улучшения тягово-сцепных свойств и экономичности автомобилей выбором оптимального передаточного числа межосевого дифференциала, необходимо констатировать, что окончательно эту задачу можно решить после проведения широких экспериментальных исследований по оценке фактических режимов работы автомобилей в различных дорожных условиях и выявлению истинного статистического распределения динамических реакций на осях и крутящих моментов, подводимых к ним, в том числе и при отборе мощности.
 

Средние значения КПД отдельных передач приведены в табл. 5.4, а рекомендации по выбору передаточных чисел — в табл. 5.5. Так как передачи с большими передаточными числами имеют большие габариты, их следует применять лишь в крайних случаях.
 

Если в системе привода с неизменным потоком возбуждения оптимальное значение передаточного числа редуктора не зависело от полного пути перемещения, то в рассматриваемой — системе эта зависимость — явно имеет место. Следовательно, выбор оптимального передаточного числа редуктора следует производить с учетом гистограммы перемещений рассматриваемого механизма.
 

Если действительный рабочий цикл совершается в растянутый период времени, то значительное количество тепла может быть удалено путем естественного охлаждения; но если рабочий цикл уплотнен в малый отрезок времени и включает высокие ускорения, то следует выбирать муфту увеличенного размера или прибегать к искусственному охлаждению. Способность муфты управлять заданной нагрузкой рассматривается в связи с выбором передаточного числа зубчатой передачи в § 14 — 7; здесь будет рассмотрена лишь энергия, рассеиваемая в муфте.