Как посчитать передаточное отношение зубчатой передачи

Планетарная передача

При производстве современных автомобилей и механизмов достаточно часто применяется планетарная схема. В данном случае речь идет про стандартный механизм, который используется для передачи и преобразования вращательных действий. Специально для этого применяются колеса с зубьями, которые помещены на перемещающиеся оси. Основными конструктивными компонентами выступают центральные колеса с зубьями, которые крепятся на осях неподвижного типа

Также здесь принимаются во внимание боковые зубчатые колеса, которые крепятся на перемещающиеся оси. Чтобы достичь максимального эффекта от такого соединения, механизмы производятся на параллельных осях. При такой схеме можно добиться максимального передаточного отношения передачи в 9 единиц

При такой схеме можно добиться максимального передаточного отношения передачи в 9 единиц.

Также у подобных механизмов очень высокий КПД, который нередко приближается к отметке в 0,98. На практике, чаще всего можно встретить изделия, где используется сразу несколько сателлитов, которые расположены с равными по величине угловыми шагами. В конечном итоге производители создают подобные конструкции с конечным иле переменным передаточным отношением. Также встречаются механизмы, где этот параметр подвергается регулировке, из-за чего из выпускают обратимыми или необратимыми.

Если говорить про обратимые конструкции, то здесь осуществляется движение только в прямом или обратном направлении. Что касается необратимых элементов, то здесь подобное движение невозможно. Что же касается передаточного отношения, то в таких вариантах изделий оно может иметь ступенчатый или бесступенчатый тип. В первом случае речь идет про механическую коробку переключения передач. Что касается второго типа, то он легко прослеживается в современных вариативных трансмиссиях. Нужно понимать, что упомянутые передаточные отношения передач в полной мере просчитываются производителями на этапе проектирования механизма, чтобы была возможность подобрать оптимальную кинетическую схему. Далее, производитель выбирает вариант соединения механизмов, а также определяет максимальную эффективность, чтобы оценить также и надежность конструкции.

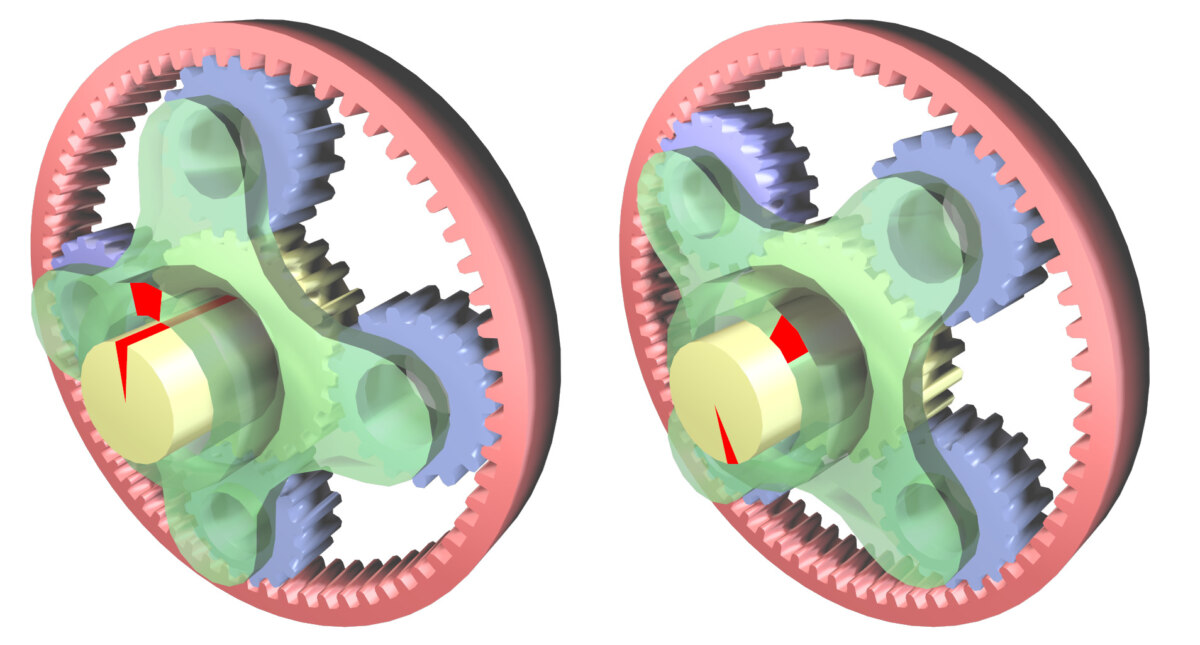
Передаточное отношение ременной передачи

Ременной передачей называют два шкива, которые соединяет ремень, как это показано на рисунке. Возможно, что она была одним из первых способов, которые применял человек. Менялся материал, используемый для изготовления ремня, менялась его форма, но неизменным оставалось передаточное отношение, определяемое как частое от деления скорости ведущего вала, на скорость ведомого, или как результат деления числа оборотов этих валов (n1/n2 или ω1/ω2).
Для ременной передачи оно может быть рассчитано с использованием диаметров (радиусов) шкивов. Передаточное число в таком случае также определяется как частное от деления оборотов.

Если при преобразовании энергии число оборотов понижается, то есть передаточное число больше 1, то передача будет понижающей, а само устройство носит название редуктора. Если результат меньше единицы, то устройство называется мультипликатором, хотя оно также выполняет функции редуктора, только понижающего. Передаточное отношение редуктора позволяет уменьшить число оборотов (угловую скорость), поступающих с ведущего вала на ведомый, увеличив при этом передаваемый момент.

Это свойство редуктора дает возможность добиваться инженерам при проектировании различных устройств изменения параметров передаваемой энергии, а передаточное отношение редуктора служит при этом мощным инструментом в решении поставленной задачи.

Несмотря на значительный возраст, для ременной передачи и сейчас находится работа на автомобиле, она используется как привод генератора, газораспределительного механизма, а также в некоторых других случаях.

Крутящий момент редуктора

Крутящий момент на выходном валу – вращающий момент на выходном валу. Учитывается номинальная мощность , коэффициент безопасности , расчетная продолжительность эксплуатации (10 тысяч часов), КПД редуктора.

Номинальный крутящий момент – максимальный крутящий момент, обеспечивающий безопасную передачу. Его значение рассчитывается с учетом коэффициента безопасности – 1 и продолжительность эксплуатации – 10 тысяч часов.

Максимальный вращающий момент – предельный крутящий момент, выдерживаемый редуктором при постоянной или изменяющейся нагрузках, эксплуатации с частыми пусками/остановками. Данное значение можно трактовать как моментальную пиковую нагрузку в режиме работы оборудования.

Необходимый крутящий момент – крутящий момент, удовлетворяющим критериям заказчика. Его значение меньшее или равное номинальному крутящему моменту.

Расчетный крутящий момент – значение, необходимое для выбора редуктора. Расчетное значение вычисляется по следующей формуле:

Mc2 = Mr2 x Sf ≤ Mn2

где Mr2 – необходимый крутящий момент; Sf – сервис-фактор (эксплуатационный коэффициент); Mn2 – номинальный крутящий момент.

Читать также: Качественные цепи для бензопил

Определение передаточного числа главной передачи.

Передаточ­ное число главной передачи находят исходя из максимальной ско­рости автомобиля на высшей передаче, заданной техническими условиями на проектируемый автомобиль.

Значение передаточного числа главной передачи определяют по формуле

Ur=3,6(wmaxrk)/VmaxUkUд

где vmax — максимальная скорость автомобиля, км/ч; wmах — мак­симальная угловая скорость коленчатого вала, рад/с; rk — радиус колеса, м; Uk — передаточное число коробки передач на высшей передаче; ид — передаточное число дополнительной коробки пе­редач на высшей передаче (ид = 1).

Полагают, что передаточные числа коробки передач на выс­шей передаче имеют следующие значения: ик= 1,0 — для прямой передачи и ик = 0,9…1,0 — для повышающей передачи легковых автомобилей; ик — 1,0 — для грузовых автомобилей с числом пере­дач не более шести; ик = 0,7…0,8 — для многоступенчатых коро­бок передач грузовых автомобилей.

Найденное расчетным путем передаточное число главной пе­редачи UТ должно иметь следующие значения: не более 5,0 — у легковых автомобилей; не более 7,0 — у грузовых автомобилей грузоподъемностью до 8 т; не более 8,0 — у грузовых автомобилей грузоподъемностью свыше 8 т.

Расчетное значение передаточного числа главной передачи не­обходимо сравнить с существующими передаточными числами главных передач автомобилей аналогичного типа и назначения. В том случае, если у новой модели автомобиля проектируется ве­дущий мост, то это значение передаточного числа уточняют с учетом числа зубьев шестерен главной передачи.

Определение передаточного числа первой передачи коробки передач. Определение передаточных чисел промежуточных ступеней коробки передач.

При опре­делении передаточных чисел коробки передач нужно помнить о том, что I передача предназначена для преодоления максималь­ного сопротивления дороги. Промежуточные передачи коробки пе­редач используются при разгоне автомобиля, преодолении повы­шенного сопротивления движению, работе автомобиля в услови­ях, не позволяющих двигаться с высокой скоростью (гололед, выбитая дорога, задержка впереди идущим транспортом и т.д.), а также при торможении двигателем на затяжных пологих спусках.

При расчете передаточных чисел сначала находят передаточ­ное число I передачи по заданному техническими условиями мак­симальному коэффициенту сопротивления дороги ψmах или мак­симальному динамическому фактору автомобиля по тяге Dmax на I передаче.

Это передаточное число определяют с помощью выражения, полученного из формулы для динамического фактора, пренебре­гая силой сопротивления воздуха, так как она незначительна при небольших скоростях движения:

u1=(Gaψmaxrk)/Mmaxηтрuгuд

где Ga — вес автомобиля с полной нагрузкой, Н; Mmax — макси­мальный крутящий момент двигателя, Н • м.

Полученное передаточное число I передачи коробки передач не гарантирует отсутствия буксования ведущих колес автомобиля. Чтобы не было буксования ведущих колес при движении на I пере­даче, необходимо выполнение следующего неравенства:

(Mmaxηтрuгuдu1)/ Gark≤Dсц=(mp2Ga2φx)/Ga

где Dсц — динамический фактор автомобиля по сцеплению; тР2 -= 1,20…1,35 — коэффициент изменения реакций на задних веду­щих колесах; Ga2 —- вес, приходящийся на задние колеса автомо­биля с полной нагрузкой, Н; фх= 0,6…0,8 — коэффициент сцеп­ления колес с дорогой.

Из этого соотношения определяют новое передаточное число I передачи, при котором буксования ведущих колес не будет:

u1=(mp2Ga2φxrk)/ Mmaxηтрuгuд

После проверки передаточного числа I передачи на отсутствие буксования ведущих колес автомобиля из двух найденных переда­точных чисел I передачи коробки передач для дальнейших расче­тов выбирают меньшее.

По этому значению передаточного числа I передачи и извест­ному значению передаточного числа высшей передачи определя­ют передаточные числа промежуточных передач.

Если высшая передача прямая (ип = 1), то для расчёта переда­точных чисел промежуточных передач используют следующее выражение:

Uk=

где п’ — число передач, не считая повышающую передачу и пере­дачу заднего хода; к — номер передачи.

Если высшая передача повышающая (ик < 1), то значение ее передаточного числа выбирают в соответствии с типом автомоби­ля, а остальные передаточные числа промежуточных передач рас­считывают с помощью приведенного выше выражения.

Передаточное число передачи заднего хода

Uзк=(1.2…..1,3)u1

Окончательное значение передаточного числа передачи задне­го хода определяют при компоновке коробки передач.

Рассчитанные передаточные числа коробки передач являются ориентировочными и при проектировании новой коробки пере­дач могут незначительно изменяться.

Что такое передаточное отношение

Очень часто для характеристики движения того или иного механизма используется такое термин, как передаточное отношение. Что это такое и в чем его суть, попробуем сейчас разобраться.

Каждый механизм характеризуется наличием входного и выходного вала и, соответственно, входных и выходных параметров, к которым, в частности, можно отнести взаимосвязанные между собой частоту вращения и угловую скорость. Двигатель всегда подключается в начале каждого устройства и передает движение на входной вал. Данный вал также называют ведущим, так как через него затем передается движение на механизм в целом и выходной (ведомый) вал в частности. При этом угловая скорость вала на выходе меняет либо свое значение, либо направление, либо то и другое. Поэтому для определения взаимосвязи или изменения характеристик вращения ведомого и ведущего валов и было некогда введено интересующее нас понятие.

Таким образом, можно утверждать, что передаточное отношение для любого механического устройства можно будет найти путем деления конечной угловой скорости на начальную. Учитывая существующую прямую зависимость между характеристиками движения вала, искомое отношение аналогичным образом находится через известные значения частот вращения валов. Так как производится деление одноименных величин, то найденный параметр не будет иметь размерности.

Передаточное отношение определяется не только для элементарных передач, но и для более сложных устройств. К ним, в частности, относятся коробки передач, многоступенчатые редукторы. Здесь возникают свои особенности расчетов. На последних устройствах остановимся более подробно.

Передаточное отношение редуктора будет зависеть от количества ступеней. Если в его состав входит только одна передача, то достаточно просто рассчитать искомое значение для нее как для простого устройства, чтобы достичь поставленной цели. Если же ступеней несколько, то общее передаточное отношение можно определять путем умножения передаточных чисел всех ступеней либо путем деления угловой скорости вала на входе в редуктор на угловую скорость на его выходе. Можно также воспользоваться знанием крутящего момента. Для этого нужно найти отношение на выходе и входе. Если оно больше единицы, то редуктор называется повышающим, если меньше – понижающим. Какой бы метод для своих расчетов вы не выбрали, во всех случаях должно получиться одно и то же числовое значение. Можно проверить правильность своих вычислений, воспользовавшись всеми перечисленными методами.

Передаточное отношение зубчатой передачи также определяется различными способами. Помимо выше перечисленных, можно также воспользоваться знанием числа зубьев на ведущем и ведомом колесах. Для этого достаточно найти отношение последнего значения и первого. Иногда в литературе подобным образом производится расчет передаточного числа, при этом отмечается, что оно не может быть меньше единицы. Однако в последнее время данные понятия слились воедино, и во многих современных учебниках по курсу «Детали машин» подобным образом рассчитывается именно отношение, а не только число. Это, по-видимому, правильно, так они фактически отражают одно и то же: как меняются входные и выходные параметры передачи, хотя изначально для определения отношения не имело значение, производится ли деление выходного параметра на выходной или наоборот.

Многие используют передаточное отношение для решения обратной задачи. Например, если мы знаем данную характеристику механизма и его входную угловую скорость, то для нахождения выходной достаточно будет умножить друг на друга названные параметры.

Надеюсь, прочитанная вами информация позволила заполнить некоторые пробелы в ваших знаниях, и вы сможете воспользоваться ею при выполнении различных инженерных расчетов.

fb.ru

Общее определение

Значение передаточного отношения у кинематических схем рассчитывается по стандартному математическому выражению. Результат получается при проведении математической операции деления значения угловой скорости ведущего вала или шестерёнки, на такой же параметр ведомого вала. Вместо этих значений используют отношение их частот вращения.

Современные кинематические схемы реализованы с использованием следующих механических соединений:

• с зубчатым зацеплением (в разных вариациях);
• червячных;
• фрикционных соединений;
• с помощью цепей;
• посредством специальных ремней;
• планетарных соединений.

Передача вращения основана на двух физических принципах: с помощью силы трения, с использованием механизмов зацепления. В зависимости от решаемой задачи механизмы изготавливаются с замедлением и ускорением. Первые называются редукторами, вторые — мультипликаторами. Обе разновидности бывают одноступенчатыми, двухступенчатыми, многоступенчатыми.

Пространственное расположение осей определяет следующие виды механизмов:

• параллельные (в них оба вала расположены параллельно друг относительно друга);
• пересекающиеся (зацепление происходит посредством пересечения);
• перекрещивающиеся механизмы (у них валы вступают в перекрестное зацепление).

Все типы механизмов бывают замедляющие и ускоряющие движение. Наиболее частое применение замедляющих конструкций объясняется более высокой скоростью используемых двигателей и необходимостью увеличить мощность выходного элемента кинематической схемы.

Таблица передаточных отношений является сводным документом. В ней приведены значения основных технических характеристик всех типов кинематических соединений.

В сводной таблице можно найти зависимость значения передаточного числа от допустимой мощности, которая передаётся конкретным видом соединения.

Планетарные зубчатые передачи

Планетарные зубчатые передачи, которые называются еще эпициклическими – это механизмы, состоящие из таких деталей, как сцепленные между собой зубчатые колеса, имеющие движущиеся геометрические оси. Зубчатые колеса такого типа иначе именуются сателлитами или планетными.

К основным конструктивным частям планетарных передач относятся следующие:

• «Солнечная» шестерня, располагающаяся в центральной части механизма
• Ведомая система «водило», предназначена для жесткой фиксации нескольких сателлитов (планетарных шестерен) друг относительно друга и имеющих одинаковый размер. Они находятся в состоянии зацепления с шестерней
• Внешнее зубчатое колесо (кольцевая шестерня), состоящая в зацеплении с шестернями планетарными (сателлитами)

Планетарные зубчатые механизмы чаще всего используются в так называемых, планетарных редукторах. Их широко применяют в дифференциалах как легковых, так и грузовых автомобилей (в том числе и тяжеловесных).

Планетарная система передач

Еще одной сферой, где они используются, является производство ручного электрического инструмента. К примеру, для обеспечения трансляции вращательного момента от двигателей шуруповертов к их рабочим частям применяются редукторы, построенные по планетарной схеме.

Для того чтобы получить большое количество передаточных чисел в различных механизмах, можно применять каскады планетарных зубчатых передач. Одним из ярчайших и наиболее наглядных примеров тому являются АКПП и МКПП различных транспортных средств.

Следует заметить, что наличие большого количества шестерней в планетарных зубчатых передачах обеспечивает меньшую нагрузку на каждый их элемент (в том числе, конечно же, и на зубья). Поэтому их применение позволяет конструкторам существенно снизить массу трансмиссионных устройств, при одновременном сохранении показателей передаваемой мощности.

Есть у планетарных зубчатых передач и некоторые недостатки. Главным из них является, пожалуй, невысокий коэффициент полезного действия тогда, когда используются достаточно большие передаточные отношения. Кроемее того, эти агрегаты достаточно «капризны» в смысле точности изготовления деталей и сборки.

Чаще всего планетарные зубчатые механизмы используются в следующих случаях:

• При необходимости разложения или сложения вращения
• Для обеспечения минимальных размеров устройств передачи вращения
• Для обеспечения больших передаточных отношений тогда, когда КПД можно пренебречь
• Для замены фрикционных муфт устройствами, более легкими в управлении
• Для обеспечения максимально возможной простоты управления многоступенчатыми коробками переключения передач

Планетарные зубчатые механизмы подразделяются на следующие разновидности:

• Передачи планетарные простые
• Передачи планетарные сложные (используются для значительных передаточных отношений)
• Коробки передач планетарные многоступенчатые
• Дифференциалы планетарного типа
• Вариаторы (фрикционно-планетарные передачи)
• Механизмы шарнирно-планетарные

При производстве всех тех устройств, которые перечислены выше, используются цилиндрические, винтовые, конические, червячные, фрикционные и цепные колеса.

Исследования свойств планетарных зубчатых передач ведется специалистами на протяжении уже многих десятков лет, причем применительно к их использованию в самых различных системах: машиностроении, металлообработке, формовке и т.п. В последние годы они стали наиболее активно применяться в прецизионных агрегатах.

Как рассчитать передаточное число

Шестерня и колесо имеют разное количество зубов с одинаковым модулем и пропорциональный размер диаметров. Передаточное число показывает, сколько оборотов совершит ведущая деталь, чтобы провернуть ведомую на полный круг. Зубчатые передачи имеют жесткое соединение. Передающееся количество оборотов в них не меняется. Это негативно сказывается на работе узла в условиях перегрузок и запыленности. Зубец не может проскользнуть, как ремень по шкиву и ломается.

Расчет без учета сопротивления

В расчете передаточного числа шестерен используют количество зубьев на каждой детали или их радиусы.

Где u12 – передаточное число шестерни и колеса;

Z2 и Z1 – соответственно количество зубьев ведомого колеса и ведущей шестерни.

Знак «+» ставится, если направление вращения не меняется. Это относится к планетарным редукторам и зубчатым передачам с нарезкой зубцов по внутреннему диаметру колеса. При наличии паразиток – промежуточных деталей, располагающихся между ведущей шестерней и зубчатым венцом, направление вращения изменяется, как и при наружном соединении. В этих случаях в формуле ставится «–».

При наружном соединении двух деталей посредством расположенной между ними паразитки, передаточное число вычисляется как соотношение количества зубьев колеса и шестерни со знаком «+». Паразитка в расчетах не участвует, только меняет направление, и соответственно знак перед формулой.

Обычно положительным считается направление движения по часовой стрелке. Знак играет большую роль при расчетах многоступенчатых редукторов. Определяется передаточное число каждой передачи отдельно по порядку расположения их в кинематической цепи. Знак сразу показывает направление вращения выходного вала и рабочего узла, без дополнительного составления схем.

Вычисление передаточного числа редуктора с несколькими зацеплениями – многоступенчатого, определяется как произведение передаточных чисел и вычисляется по формуле:

Способ расчета передаточного числа позволяет спроектировать редуктор с заранее заданными выходными значениями количества оборотов и теоретически найти передаточное отношение.

Зубчатое зацепление жесткое. Детали не могут проскальзывать относительно друг друга, как в ременной передаче и менять соотношение количества вращений. Поэтому на выходе обороты не изменяются, не зависят от перегруза. Верным получается расчет скорости угловой и количества оборотов.

КПД зубчатой передачи

Для реального расчета передаточного отношения, следует учитывать дополнительные факторы. Формула действительна для угловой скорости, что касается момента силы и мощности, то они в реальном редукторе значительно меньше. Их величину уменьшает сопротивление передаточных моментов:

• трение соприкасаемых поверхностей;
• изгиб и скручивание деталей под воздействием силы и сопротивление деформации;
• потери на шпонках и шлицах;
• трение в подшипниках.

Для каждого вида соединения, подшипника и узла имеются свои корректирующие коэффициенты. Они включаются в формулу. Конструктора не делают расчеты по изгибу каждой шпонки и подшипника. В справочнике имеются все необходимые коэффициенты. При необходимости их можно рассчитать. Формулы простотой не отличаются. В них используются элементы высшей математики. В основе расчетов способность и свойства хромоникелевых сталей, их пластичность, сопротивление на растяжение, изгиб, излом и другие параметры, включая размеры детали.

Что касается подшипников, то в техническом справочнике, по которому их выбирают, указаны все данные для расчета их рабочего состояния.

При расчете мощности, основным из показателей зубчатых зацепления является пятно контакта, оно указывается в процентах и его размер имеет большое значение. Идеальную форму и касание по всей эвольвенте могут иметь только нарисованные зубья. На практике они изготавливаются с погрешностью в несколько сотых долей мм. Во время работы узла под нагрузкой на эвольвенте появляются пятна в местах воздействия деталей друг на друга. Чем больше площадь на поверхности зуба они занимают, тем лучше передается усилие при вращении.

Все коэффициенты объединяются вместе, и в результате получается значение КПД редуктора. Коэффициент полезного действия выражается в процентах. Он определяется соотношением мощности на входном и выходном валах. Чем больше зацеплений, соединений и подшипников, тем меньше КПД.

Выбор — передаточное число

Выбор передаточных чисел основной и дополнительной коробок передач производится при тяговом расчете автомобиля.
 

Выбор передаточного числа зависит от требуемой скорости движения автомобиля и мощности двигателя. У легковых автомобилей передаточное число колеблется в пределах от 3 2: 1 до 6 2: 1, у грузовых автомобилей — от 5 2: 1 до 7 5: I, а иногда и выше.
 

При выборе передаточного числа следует избегать общих множителей между числом ходов червяка и числом зубьев червячного колеса. В этом случае с помощью цилиндрической фрезы получают более чистую боковую поверхность и более высокую точность в положении начальной окружности червячного колеса, а также более благоприятные условия для работы и меньшего износа червячной передачи.
 

Вопрос о выборе передаточного числа мультипликатора представляет собой отдельную задачу.
 

Некоторые рекомендации по выбору передаточных чисел помещены в табл. 6.4. Наибольшие значения передаточных чисел следует принимать лишь в крайних случаях, так как передачи с наибольшими значениями i имеют большие габариты.
 

Может быть несколько причин, вызывающих желательность выбора передаточного числа у нижнего предела допустимых значений. Например, если нагрузка от трения составляет небольшую часть от общей нагрузки, то зубчатая передача может быть сделана более простой и экономичной.
 

К этим значениям и следует стремиться путем выбора передаточного числа кинематической схемы соединения электромагнита с исполнительным устройством при заданной противодействующей характеристике последнего и заданных размерах полюсного наконечника.
 

Вторым шагом при предварительном выборе основных параметров электропривода является выбор передаточного числа / редуктора, связывающего основной вал проектируемого механизма с двигателем.
 

Приведенные оптимальные передаточные числа являются лишь отправными величинами при выборе рабочего передаточного числа. Последнее выбирается после производства ряда расчетов с различными передаточными числами и сопоставления результатов с учетом максимально допустимой скорости механизма и требуемой мощности двигателя.
 

Если для привода используется высокоскоростной двигатель, то возникает проблема выбора передаточного числа механизма, связывающего двигатель с исполнительным звеном.
 

Таким образом, отмечая возможность улучшения тягово-сцепных свойств и экономичности автомобилей выбором оптимального передаточного числа межосевого дифференциала, необходимо констатировать, что окончательно эту задачу можно решить после проведения широких экспериментальных исследований по оценке фактических режимов работы автомобилей в различных дорожных условиях и выявлению истинного статистического распределения динамических реакций на осях и крутящих моментов, подводимых к ним, в том числе и при отборе мощности.
 

Средние значения КПД отдельных передач приведены в табл. 5.4, а рекомендации по выбору передаточных чисел — в табл. 5.5. Так как передачи с большими передаточными числами имеют большие габариты, их следует применять лишь в крайних случаях.
 

Если в системе привода с неизменным потоком возбуждения оптимальное значение передаточного числа редуктора не зависело от полного пути перемещения, то в рассматриваемой — системе эта зависимость — явно имеет место. Следовательно, выбор оптимального передаточного числа редуктора следует производить с учетом гистограммы перемещений рассматриваемого механизма.
 

Кривые статической характеристики муфты типа свключено — выключено. а — момент в функции скорости. б — момент в функции сигнала управления.| Видоизмененная характеристика момент — сигнал управления ( с учетом гистерезиса муфты типа включено — выключено.| Кривые нелинейных статических Характеристик, типичные для некоторых муфт вихревых токов и фрикционно-дисковых муфт. а — момент в функции скорости. о — момент в функции сигнала управления.

Если действительный рабочий цикл совершается в растянутый период времени, то значительное количество тепла может быть удалено путем естественного охлаждения; но если рабочий цикл уплотнен в малый отрезок времени и включает высокие ускорения, то следует выбирать муфту увеличенного размера или прибегать к искусственному охлаждению. Способность муфты управлять заданной нагрузкой рассматривается в связи с выбором передаточного числа зубчатой передачи в § 14 — 7; здесь будет рассмотрена лишь энергия, рассеиваемая в муфте.
 

Калькулятор КПП и главной пары

R колеса
Ширина колеса
Профиль
Обороты двигателя	500100015002000250030003500400045005000550060006500700075008000850090009500100001050011000
Главная пара	3.9 3.5 3.74.14.34.54.74.95.16.8
1-я передача	3.63 (станд.) 2.92 (5-й ряд)2.92 (6-й ряд) 2.92 (7-й ряд)3.42 (8-й ряд) 3.42 (10-й ряд)3.63 (11-й ряд) 3.16 (12-й ряд) 3.17 (15-й ряд)3.17 (18-й ряд) 3.17 (20-й ряд)3.17 (102-й ряд)2.92 (103-й ряд)2.92 (104-й ряд)2.92 (200-й ряд)3.0 (026-й ряд) 3.0 (711-й ряд) 2.67 (745-й ряд)2.67 (74-й ряд)
2-я передача	1.95 (станд.)1.81 (5-й ряд)1.81 (6-й ряд)2.05 (7-й ряд)2.05 (8-й ряд)2.05 (10-й ряд)2.22 (11-й ряд)1.95 (12-й ряд)1.81 (15-й ряд)2.11 (18-й ряд)1.9 (20-й ряд)1.95 (102-й ряд)1.95 (103-й ряд)1.95 (104-й ряд)2.22 (200-й ряд)2.53 (026-й ряд) 2.53 (711-й ряд) 1.93 (745-й ряд)1.93 (74-й ряд)
3-я передача	1.36 (станд.)1.28 (5-й ряд)1.28 (6-й ряд)1.56 (7-й ряд)1.36 (8-й ряд)1.36 (10-й ряд)1.54 (11-й ряд)1.36 (12-й ряд)1.28 (15-й ряд)1.48 (18-й ряд)1.26 (20-й ряд)1.36 (102-й ряд)1.36 (103-й ряд)1.36 (104-й ряд)1.76 (200-й ряд)2.06 (026-й ряд) 2.06 (711-й ряд) 1.59 (745-й ряд)1.56 (74-й ряд)
4-я передача	0.94 (станд.)0.97 (5-й ряд)1.06 (6-й ряд)1.31 (7-й ряд)0.97 (8-й ряд)0.97 (10-й ряд)1.17 (11-й ряд)1.03 (12-й ряд)0.94 (15-й ряд)1.13 (18-й ряд)0.94 (20-й ряд)0.94 (102-й ряд)0.94 (103-й ряд)1.03 (104-й ряд)1.39 (200-й ряд)1.74 (026-й ряд) 1.74 (711-й ряд) 1.37 (745-й ряд)1.37 (74-й ряд)
5-я передача	0.78 (станд.)0.78 (5-й ряд)0.94 (6-й ряд)1.13 (7-й ряд)0.78 (8-й ряд)0.78 (10-й ряд)0.89 (11-й ряд)0.78 (12-й ряд)0.73 (15-й ряд)0.89 (18-й ряд)0.73 (20-й ряд)0.73 (102-й ряд)0.69 (103-й ряд)0.73 (104-й ряд)1.17 (200-й ряд)1.48 (026-й ряд) 1.48 (711-й ряд) 1.2 (745-й ряд)0.79 (74-й ряд)
6-я передача	нет0.69 (станд.)0.94 (7-й ряд)0.78 (18-й ряд)0.94 (200-й ряд)
Результаты:

martaler.ru

3.6. Определение общего передаточного отношения заданного привода, а также простой и планетарной ступени зубчатого механизма.

Зубчатый ряд – механизм, в который входит два и более зубчатых колёс.

В зубчатом ряду колёса могут быть:

— ведущими – получают движение через вал, передают через зыбья;

— ведомыми – получают движение через зубья, передают через вал;

— промежуточные – получают и передают движения через зубья;

Передаточное отношение зубчатого ряда равно произведению передаточных отношений отдельных ступеней зубчатого ряда (равно дроби, в числителе которой записываем произведение чисел зубьев ведомых колёс, а в знаменателе – произведение чисел зубьев ведущих колёс).

Знак передаточного отношения зубчатого ряда будет (+), если число внешних зацеплений будет чётное; (-) – число зацеплений нечётное. Промежуточные колёса на величину передаточного отношения не влияют, но влияют на знак.

Эпициклическими – называются зубчатые механизмы с подвижными осями зубчатых колес. Эпициклические механизмы делятся на: планетарные (W=1) и дифференциальные (W>1).

Опорным – называется неподвижное центральное колесо.

Признаки планетарного механизма:

сателлиты и вадило (рычаг, который связан с сателлитом), наличие центрального (солнечного) неподвижного колеса.

Назначение планетарных механизмов – передача движения с заданным передаточным отношением. Назначение дифференциальных механизмов – сложение или разложение движений.

Обращённым – называется механизм (условный), который получается, если условно остановить водило, а угловые скорости всех остальные зубчатых колёс уменьшить на величину угловой скорости водила, тогда обращённый механизм представляет собой простой зубчатый ряд.

Комбинированный механизм – механизм, в состав которого входит одна или несколько планетарных ступеней или планетарная ступень и простые зубчатые ряды. Передаточное отношение комбинированного механизма определяется как произведение передаточных отношений отдельных ступеней этого механизма.

Замкнутым дифференциалом – называется зубчатый механизм, дифференциальная часть которого соединяется дополнительной кинематической цепью, представляющую собой чаще всего простой зубчатый ряд (W=1).

Вычерчиваем схему планетарного редуктора:

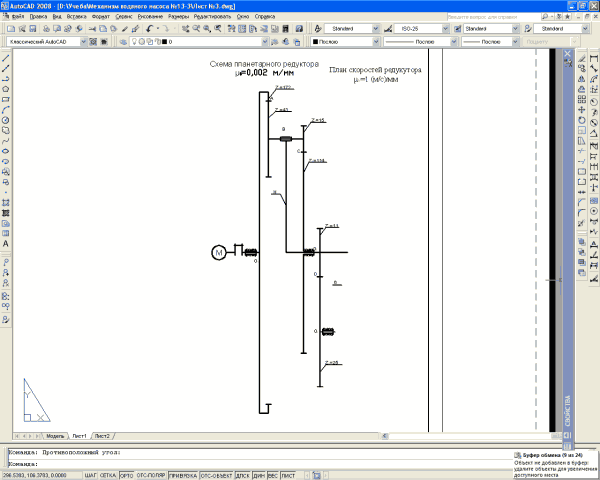
Рис.3.6.1. Схема планетарного редуктора.

Знак передаточного отношения – «+»;

m=10 мм; z₅=11; z₆=25;

По формуле Виллиса:

Для определения передаточного отношения планетарного механизма правую часть формулы Виллиса необходимо почленно на угловую скорость выходного планетарного механизма, и из полученного выражения определить требуемое передаточное отношение.

При синтезе планетарного механизма за основное условие принимали заданное передаточное отношение; в качестве дополнительного – условие соосности. Исходя из этих условий, подбираем числа зубьев всех колёс.

Проверяем, выполняется ли условие соосности.

Рассчитываем радиусы делительных окружностей:

Z₁=172

Z₂=43

Z₃=15

Z₄=114

Для построения планетарного редуктора выберем масштабный коэффициент:

При синтезе планетарного механизма, в качестве дополнительного условия может быть также ипоьзовано:

1. условие соседства:

когда для обеспечения прочности и жёсткости зубчатого механизма, в редуктор устанавливается несколько сателлитов.

₂₁

1. условие сборки:

заключается в том, что при установке первого сателлита, солнечные колёса займут вполне определённое положение и может случиться так, что при установке следующего сателлита его зубья наложаться на зубья одного из центральных колёс, что воспрепятствует сборке.

условие:

₁₃

Сумма центральных солнечных колёс должна быть кратной числу сателлитов.

StudFiles.ru