Погрешность измерения

Введение

Все, что сказано в этом введении, запоминать не нужно. это справочный материал, к которому вы будете обращаться при выполнении лабораторных работ.

1. Как определять погрешности измерений

Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.

Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.

Прямое измерение — определение значения физической величины непосредственно средствами измерения.

Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.

Введем следующие обозначения:

A, B, C, … — физические величины.

A_пр — приближенное значение физической величины, т.е. значение, полученное путем прямых или косвенных измерений.

ΔA — абсолютная погрешность измерения физической величины.

ε — относительная погрешность измерения физической величины, равная:

Δ_иA — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; указывается в каждой работе при описании прибора в разделе Оборудование и средства измерения)

Δ_оA — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения), она равна в большинстве случаев половине цены деления; при измерении времени — цене деления секундомера или часов.

Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:

ΔA=Δ_иA + Δ_оA

Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔA≈0,17=0,2); численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А=10,332≈10,3).

Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, отличаются друг от друга.

В этом случае A_пр находят как среднее арифметическое значение всех измерений, а ΔA (ее в этом случае называют случайной погрешностью) определяют методами математической статистики.

В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. При этом для получения результата достаточно одного измерения.

Относительная погрешность косвенных измерений определяется, как показано в таблице 1.

Абсолютная погрешность косвенных измерений определяется по формуле ΔA=A_прε (ε выражается десятичной дробью).

Таблица 1

Формулы для нахождения относительной погрешности косвенных измерений

Nº п/п	Формула физической величины	Формула относительной погрешности
1
2
3	A=B+C
4

2. О классе точности электроизмерительных приборов

Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γ_пр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность Δ_иA от всей шкалы прибора (A_max):

Класс точности указывается при описании прибора в разделе Оборудование и средства измерения. Cуществуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γ_пр) и всю его шкалу (A_max), определяют абсолютную погрешность Δ_иA измерения физической величины А этим прибором:

3. Как сравнивать результаты измерений

1. Записать результаты измерений в виде двойных неравенств:

A_{1 пр} – ΔA₁ < A_{1 пр} < A_{1 пр} + ΔA₁A_{2 пр} – ΔA₂ < A_{2 пр} < A_{2 пр} + ΔA₂
2. Сравнить полученные интервалы значений (рис.1): если интервалы не перекрываются, то результаты неодинаковы, если перекрываются — одинаковы при данной относительной погрешности измерений.

Рисунок 1.

4. Как оформлять отчет о проделанной работе

Отчетом о проделанной работе является форма, находящаяся в левом нижнем окне. После ее заполнения надо нажать на кнопку «Отправить результаты на сервер».

Значения измеренных физических величин переносятся в таблицу результатов автоматически после нажатия соответствующей кнопки.

Значения остальных величин и ответ на контрольный вопрос вводятся с клавиатуры.

домашней странице BARSIC

Методы Корнфельда и Стьюдента

Некоторые экспериментальные исследования требуют многократного измерения одного и того же показателя с помощью аппаратуры или приспособлений. В этом случае высока вероятность возникновения отклонений разброса. Определить ее величины можно разными способами. Самый распространенный и доступный из них называется по автору — методом Корнфельда.

Он применяется в ситуации, когда какая-либо физическая величина была измерена n раз. В этом случае рекомендован следующий порядок действий:

1. Предполагается, что имеется ряд результатов измерений от Х1 до Хn.
2. Из этих величин выбирают минимальную и максимальную.
3. Вычисляют среднее значение Х.
4. В пределах от наименьшего до наибольшего показателя выбирают доверительный интервал.
5. Чтобы найти абсолютное отклонение, необходимо вычесть из максимального результата измерения величину минимального. Полученную разность делят пополам.

Метод Корнфельда имеет существенный недостаток. Чтобы определить вероятность приведенного результата, необходимо провести большое количество измерений. При этом нет возможности изменить границы доверительного интервала. Более точные данные можно получить, используя метод расчета Стьюдента. Для этого используют специальные таблицы, где отражены так называемые коэффициенты Стьюдента.

Точность

Термин точность используется для выражения случайности измерительной ошибки. Случайная природа отклонений измеряемых значений в большинстве случае имеет тепловую природу. Из-за случайной природы этого шума не возможно получить абсолютную ошибку. Точность дается только вероятностью того, что измеряемая величина лежит в некоторых пределах.

Распределение Гаусса

Тепловой шум имеет гауссово, или, как еще говорят, нормальное распределение. Оно описывается следующим выражением:

Здесь  — среднее значение, показывает дисперсию и соответствует RMS-значению шумового сигнала. Функция дает кривую распределения вероятностей, как показано на рисунке ниже, где среднее значение и эффективная амплитуда шума .

Распределение вероятностей с и

В таблице указаны шансы получения значений в заданных пределах.

Граница	Шанс
0.5·σ	38.3 %
0.674·σ	50.0 %
1·σ	68.3 %
2·σ	95.4 %
3·σ	99.7 %

Как видно, вероятность того, что измеренное значение лежит в диапазоне ± равна .

Повышение точности

Точность может быть улучшена передискретизацией (изменением частоты дискретизации) или фильтрацией. Отдельные измерения усредняются, поэтому шум значительно снижается. Также снижается разброс измеренных значений. Используя передискретизацию или фильтрацию необходимо учитывать, что это может привести к снижению пропускной способности.

1.2 Многократные измерения

Проведём серию из nодинаковых (однотипных) измерений одной
и той же физической величины (например, многократно приложим линейку к стержню) и получим
ряд значений

𝐱={x1,x2,…,xn}.

Что можно сказать о данном наборе чисел и о длине стержня?
И можно ли увеличивая число измерений улучшить конечный результат?

Если цена деления самой линейки достаточно мала, то как нетрудно убедиться
на практике, величины {xi} почти наверняка окажутся
различными. Причиной тому могут быть
самые разные обстоятельства, например: у нас недостаточно остроты
зрения и точности рук, чтобы каждый раз прикладывать линейку одинаково;
стенки стержня могут быть слегка неровными; у стержня может и не быть
определённой длины, например, если в нём возбуждены звуковые волны,
из-за чего его торцы колеблются, и т. д.

В такой ситуации результат измерения интерпретируется как
случайная величина, описываемая некоторым вероятностным законом
(распределением).
Подробнее о случайных величинах и методах работы с ними см. гл. .

По набору результатов 𝐱 можно вычислить их среднее арифметическое:

⟨x⟩=x1+x2+…+xnn≡1n⁢∑i=1nxi.

(1.1)

Это значение, вычисленное по результатам конечного числа n измерений,
принято называть выборочным средним. Здесь и далее для обозначения
выборочных средних будем использовать угловые скобки.

Кроме среднего представляет интерес и то, насколько сильно варьируются
результаты от опыта к опыту. Определим отклонение каждого измерения от среднего как

Δ⁢xi=xi-⟨x⟩,i=1⁢…⁢n.

Разброс данных относительно среднего принято характеризовать
среднеквадратичным отклонением:

s=Δ⁢x12+Δ⁢x22+…+Δ⁢xn2n=1n⁢∑i=1nΔ⁢xi2

(1.2)

или кратко

s2=⟨(x-⟨x⟩)2⟩.

(1.3)

Значение среднего квадрата отклонения s2 называют
выборочной дисперсией.

Будем увеличивать число измерений n (n→∞). Если объект измерения и методика
достаточно стабильны, то отклонения от среднего Δ⁢xi будут, во-первых,
относительно малы, а во-вторых, положительные и отрицательные отклонения будут
встречаться примерно одинаково часто. Тогда при вычислении ()
почти все отклонения Δ⁢xi скомпенсируются и можно ожидать,
что выборочное среднее при n≫1 будет стремиться к некоторому пределу:

limn→∞⁡1n⁢∑i=1nxi=x¯.

Тогда предельное значение x¯ можно отождествить с «истинным» средним
для исследуемой величины.

Предельную величину среднеквадратичного отклонения при n→∞
обозначим как

limn→∞⁡1n⁢∑i=1nΔ⁢xi2=σ.

Замечание. В общем случае указанные пределы могут и не существовать. Например, если измеряемый параметр
меняется во времени или в результате самого измерения, либо испытывает слишком большие
случайные скачки и т. п. Такие ситуации требуют особого рассмотрения и мы на них не
останавливаемся.

Замечание. Если n мало (n<10), для оценки среднеквадратичного отклонения
математическая статистика рекомендует вместо формулы () использовать
исправленную формулу (подробнее см. п. ):

sn-12=1n-1⁢∑i=1nΔ⁢xi2,

(1.4)

где произведена замена n→n-1. Величину sn-1
часто называют стандартным отклонением.

Итак, можно по крайней мере надеяться на то, что результаты небольшого числа
измерений имеют не слишком большой разброс, так что величина ⟨x⟩
может быть использована как приближенное значение (оценка) истинного значения
⟨x⟩≈x¯,
а увеличение числа измерений позволит уточнить результат.

Многие случайные величины подчиняются так называемому нормальному закону
распределения (подробнее см. Главу ). Для таких величин
могут быть строго доказаны следующие свойства:

• •

  при многократном повторении эксперимента бо́льшая часть измерений
  (∼68%) попадает в интервал x¯-σ<x<x¯+σ
  (см. п. ).

• •

  выборочное среднее значение ⟨x⟩ оказывается с большей
  вероятностью ближе к истинному значению x¯, чем каждое из измерений
  {xi} в отдельности. При этом ошибка вычисления среднего
  убывает пропорционально корню из числа опытов n
  (см. п. ).

ВЕСА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ

При неравноточных измерениях, когда результаты каждого измерения нельзя считать одинаково надежными, уже нельзя обойтись определением простого арифметического среднего. В таких случаях учитывают достоинство (или надежность) каждого результата измерений.Достоинство результатов измерений выражают некоторым числом, называемым весом этого измерения. Очевидно, что арифметическое среднее будет иметь больший вес по сравнению с единичным измерением, а измерения, выполненные при использовании более совершенного и точного прибора, будут иметь большую степень доверия, чем те же измерения, выполненные прибором менее точным.
Поскольку условия измерений определяют различную величину средней квадратической погрешности, то последнюю и принято принимать в качестве основы оценки весовых значений, проводимых измерений. При этом веса результатов измерений принимают обратно пропорциональными квадратам соответствующих им средних квадратических погрешностей.
Так, если обозначить через р и Р веса измерений, имеющие средние квадратические погрешности соответственно m и µ, то можно записать соотношение пропорциональности:

Например, если µ средняя квадратическая погрешность арифметического среднего, а m – соответственно, одного измерения, то, как следует из

можно записать:

т. е. вес арифметического среднего в n раз больше веса единичного измерения.

Аналогичным образом можно установить, что вес углового измерения, выполненного 15-секундным теодолитом, в четыре раза выше веса углового измерения, выполненного 30-секундным прибором.

При практических вычислениях обычно вес одной какой-либо величины принимают за единицу и при этом условии вычисляют веса остальных измерений. Так, в последнем примере если принять вес результата углового измерения 30-секундным теодолитом за р = 1, то весовое значение результата измерения 15-секундным теодолитом составит Р = 4.

Понятие и классификация

Под термином погрешность принято понимать степень отклонения реальной величины от вычисленной. Этот показатель служит мерой точности измерения.

Существует несколько разновидностей погрешности:

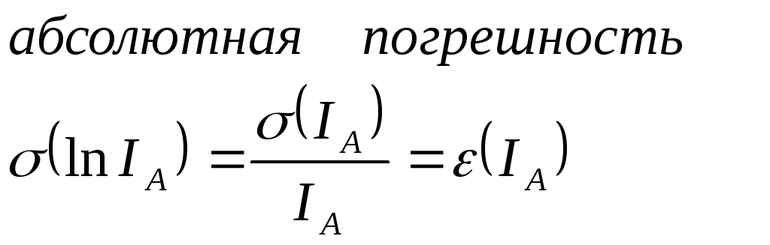
1. Абсолютная — оценка ошибки в абсолютных единицах. Величина ее может быть разной в зависимости от способа расчета.
2. Относительная — отношение абсолютной величины к тому значению, которое принято считать истинным. Измеряется в процентах.
3. Приведенная — разновидность относительной. Ее вычисляют отношением абсолютной и условной постоянной величины, определяется в процентах.
4. Приборная или инструментальная — погрешность, которую дают технические средства измерений. Она обусловлена неточной цифровой градуировкой приборов или недостаточной наглядностью. Класс точности приборов будет равен максимальной приведенной погрешности и выражается в процентах. К примеру, класс точности вольтметра ΔU = ±0,75 В.
5. Методическая — связанная с несовершенством метода измерения или его чрезмерным упрощением.
6. Субъективная или операторная — погрешность, связанная с личными свойствами оператора — невнимательностью, утомлением, профессиональной подготовленностью.
7. Случайная. Погрешность, которая может изменяться при разных измерениях. Изменения возможны по знаку или величине отклонения. Причиной может быть техническое несовершенство приборов отсчета или объекта измерения, неблагоприятные для работы условия или особенности измеряемых единиц.
8. Систематическая. Погрешность, изменения которой имеют некоторую закономерность во времени. В качестве частного случая допускают постоянное отклонение, которое не изменяется во времени.
9. Прогрессирующая или дрейфовая — медленно изменяется во времени и не может быть предсказана. Такое отклонение относится к случайным.
10. Грубая или промах. Значительное отклонение от принятой нормы. Возникает в результате неисправности аппаратуры или ошибки экспериментатора.

Разрешение

Разрешением, или, как еще говорят, разрешающей способностью измерительной системы является наименьшая различимая измеряемая величина. Определение разрешения прибора не относится к точности измерения.

Цифровые измерительные системы

Цифровая система преобразует аналоговый сигнал в цифровой эквивалент посредством аналого-цифрового преобразователя. Разница между двумя значениями, то есть разрешение, всегда равно одному биту. Или, в случае с цифровым мультиметром, это одна цифра.

Возможно также выразить разрешение через другие единицы, а не биты. В качестве примера рассмотрим цифровой осциллограф, имеющий 8-битный АЦП. Чувствительность по вертикали установлена в 100 мВ/дел и число делений равно 8, полный диапазон, таким образом, равен 800 мВ. 8 бит представляются 28=256 различными значениями. Разрешение в вольтах тогда равно 800 мВ / 256 = 3125 мВ.

Аналоговые измерительные системы

В случае аналогового прибора, где измеряемая величина отображается механическим способом, как в стрелочном приборе, сложно получить точное число для разрешения. Во-первых, разрешение ограничено механическим гистерезисом, причиной которого является трение механизма стрелки. С другой стороны, разрешение определяется наблюдателем, делающем свою субъективную оценку.

Абсолютная и относительная погрешность

Абсолютной погрешностью или, короче, погрешностью приближенного
числа называется разность между этим числом и его точным значением (из большего числа вычитается меньшее)*.

Пример 1. На предприятии 1284 рабочих и служащих. При
округлении этого числа до 1300 абсолютная погрешность
составляет 1300 — 1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 — 1280 = 4.

Относительной погрешностью приближенного числа называется отношение
абсолютной погрешности приближенного числа к самому этому числу.

Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная
погрешность составляет 200 — 197 = 3. Относительная погрешность равна 3/197 или, округленно, 3/197 = 1,5 %.

В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности.
Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.

Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза
неизвестен. Но абсолютная погрешность не
превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈ 1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью. Число, заведомо превышающее
относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.

В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность — 1,4 %.

Величина предельной погрешности не является вполне определенной. Так, в примере 3 можно принять за предельную абсолютную
погрешность 100 г, 150 г и вообще всякое число, большее чем 50 г. На практике берется по возможности меньшее значение
предельной погрешности. В тех случаях, когда известна точная величина погрешности, эта величина служит одновременно
предельной погрешностью. Для каждого приближенного числа должна быть известна его предельная погрешность
(абсолютная или oотносительная). Когда она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания
предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого
соглашения всегда можно обойтись без указания предельной погрешности числа.

Предельная абсолютная погрешность обозначается греческой буквой Δ («дельта»); предельная относительная
погрешность — греческой буквой δ («дельта малая»). Если приближенное число обозначить буквой а, то

δ = Δ/a.

Пример 4. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная
относительная погрешность этого измерения?
Здесь а = 17,9 см; можно принять Δ = 0,1 см, так как с точностью до 1 мм измерить карандаш нетрудно, a значительно уменьшить, предельную погрешность ни удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого карандаша ребра могут разниться на бoльшую величину). Относительная погрешность равна 0,1/17,9.
Округляя, находим δ = 0,1/18 ≈ 0,6%.

Пример 5. Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы
предельная относительная погрешность составляла 0,05%?Решение. По условию, предельная абсолютная погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная
абсолютная погрешность равна 36*(0,05/100) = 0,0175 (мм) или, усиливая, 0,02 (мм). Можно воспользоваться
формулой δ = Δ/a.
Подставляя в неё а = 35, δ = 0,0005, имеем 0,0005 = Δ/35. Значит, Δ = 35 • 0,0005 = 0,0175 (мм).

* Иначе говоря, если a есть приближенное число, а х – его точное значение, то абсолютная погрешность есть абсолютное
значение разности a – х. В некоторых руководствах абсолютной погрешностью называется сама
разность a – х (или разность х — a). Эта величина может быть положительной или отрицательной.

30 Поверка и калибровка си. Определения. Правовые основы.

В
соответствии с законом РК «Об обеспечении
единства измерений» введе­ны следующие
понятия:

— поверка
средства измерений —
совокупность операций, выполняемых
органа­ми Государственной метрологической
службы (другими уполномоченными на то
органами, организациями) с целью
определения и подтверждения соответ­ствия
средства измерений установленным
требованиям;

— калибровка
средств измерений —
совокупность операций, выполняемых с
це­лью определения и подтверждения
действительных значений метрологических
характеристик и/или пригодности к
применению средства измерений, не
под­лежащего государственному
метрологическому контролю и надзору.

В
обоих случаях, как при поверке, так и
при калибровке, определяются метрологические
характеристики средств измерений,
причем часто по одной и той же методике,
называемой методикой
поверки,
но на этом их сходство заканчивается. Различия
между этими понятиями имеют
более принципиальный характер.

Во-первых,
в сферах распространения ГМКиН могут
применяться только поверенные СИ, а
калиброванные — не могут.

Во-вторых,
поверке могут подвергаться только СИ
утверж­денного типа, то есть внесенные
в Государственный реестр СИ, а калибровке
— любые, в том числе нестандартизованные
и изготовленные в од­ном экземпляре.

В-третьих,
при поверке проверяется соответствие
СИ своему типу, внесенному в Государственный
реестр, тогда как при калибровке
опреде­ляются действительные
метрологические характеристики, которые
прибор име­ет на момент калибровки.

Если
при поверке СИ обнаружено его несоответствие
хотя бы одному пункту утвержденного
типа, средство измерений должно быть
забраковано. При калибровке этому СИ
будут приписаны новые значения
метро­логических характеристик.

Положительные
результаты поверки удостоверяются
поверительным клеймом или свидетельством
о поверке. Если средство измерений по
результатам поверки признано непригодным
к применению, оттиск поверительного
клейма и свиде­тельство о поверке
аннулируются и выписывается извещение
о непригодности или делаются соответствующие
записи в технической документации.

Результаты
калибровки удостоверяются калибровочным
знаком (клеймом), наносимым на средство
измерений, или сертификатом о калибровке,
а также, записью в эксплуатационных
документах. В соответствии с законом
РК «Об обеспечении единства измерений»
калибровка средств измерений является
процедурой добровольной и осуществляемой
по желанию владельца прибора с це­лью,
например, получения достоверных
результатов измерений, влияющих, в
конечном счете, на результаты труда.
ГМКиН на такие средства измерений не
распространяется.

Средняя квадратическая ошибка

_______Точность результатов измерений оценивается средней квадратической ошибкой. Средняя квадратическая ошибка одного измерения вычисляется по формуле:

где – сумма квадратов вероятнейших ошибок; n – число измерений. Средняя квадратическая ошибка арифметической середины вычисляется по формуле:

_______Предельная ошибка не должна превышать утроенной средней квадратической ошибки, т.е. ε = 3 x m.

_______Иногда о точности измерений судят не по абсолютной величине средней квадратической или предельной погрешности, а по величине относительной ошибки.
___

_______Относительной ошибкой называется отношение абсолютной ошибки к значению самой измеренной величины. Относительную ошибку выражают в виде простой дроби, числитель которой — единица, а знаменатель — число, округленное до двух-трех значащих цифр с нулями. Например, относительная средняя квадратическая погрешность
измерения линии длиной:

_______l = 110 м, при m = 2 см, равна m/l = 1/5500.

_______Пример:

_______Линия измерена шесть раз. Определить ее вероятнейшую длину и оценить точность этого результата. Вычисления приведены в таблице:

Таб. 1

_______По формулам вычислены абсолютные средние квадратические ошибки, а оценивать
точность измерения длины линии необходимо по относительной ошибке. Поэтому нужно абсолютную ошибку разделить на длину линии. Для нашего примера относительная
ошибка вероятнейшего значения измеренной линии равна

Максимальная абсолютная погрешность

Процесс зфавновсшивагия в цифровых приборах развертывающего уравновеши.

В цифровых циклических приборах выходной код N приближается к искомому отсчету Nх с одной стороны, сверху или снизу, поэтому при АХп ч 0 максимальная абсолютная погрешность от квантования равна ступени & хк.
 

Здесь: Арн — максимальная абсолютная погрешность величины рн, равная половине единицы разряда последней значащей цифры в табличном значении рн; Ар и АГ — максимальные абсолютные погрешности измерения р и Т соответственно.
 

Абсолютная погрешность температурного предела смеси при использовании в расчете надежных экспериментальных данных по давлению пара чистых компонентов, растворимости и коэффициентам активности, как правило, не превышает максимальной абсолютной погрешности температурного предела компонентов смеси.
 

Абсолютная погрешность при изображении в ячейке чисел с запятой, фиксированной после определенного разряда, не превосходит по величине единицы младшего разряда, то есть, как говорят, максимальная абсолютная погрешность при этом постоянна. https://spb-evacuator.ru.
 

Для учета в модели однократной экстракции NRTL влияния воды, были дополнительно подобраны эмпирические коэффициенты бинарного взаимодействия воды с компонентами системы, применение которых при численных исследованиях существенно уменьшило погрешности моделирования в области содержания воды в экстрагенте выше 8 % об. По выходу рафината и содержанию в нем аренов максимальные абсолютные погрешности в этой области составляют 0 6 и 0 9 %, соответственно. Погрешности расчета по выходу экстракта и содержания в нем аренов снизились до 0 6 и 1 1 %, что составляет 4 8 и 1 4 % относительной по.
 

Следует отметить, что для измерения среднего фазового сдвига рассмотренным методом характерно уменьшение погрешности дискретности по сравнению с имеющей место при измерении одиночного интервала времени. Хотя максимальная абсолютная погрешность дискретности определения длительности одного интервала АГ составляет ГСЧ, результирующая погрешность за время измерения Ткзм уменьшается, так как результаты измерения всех k интервалов АГ суммируются, а возникновение частотной погрешности дискретности положительного или отрицательного знака равновероятно.
 

Рассмотрим погрешность от квантования. Следовательно, максимальная абсолютная погрешность от квантования будет равна единице.
 

Второй способ сводится к увеличению числа импульсов, заполняющих временные ворота, достигаемому умножением частоты исследуемого сигнала. При этом максимальная абсолютная погрешность меняется ( если неизменна длительность ворот), но уменьшается относительная погрешность. Осуществление данного способа сопряжено с применением дополнительного блока — умножителя частоты, что усложняет и удорожает аппаратуру.
 

Максимальную погрешность Дгд Т0 удобно учитывать через эквивалентное случайное изменение числа счетных импульсов Nx на 1 импульс. При этом максимальная абсолютная погрешность дискретизации может быть определена разностью значений частоты / получаемых по формулам (7.4) или (7.5) при Л 1 и Nx, и равна А.
 

Максимальные абсолютные погрешности показаний манометров Мп и Мв, исправленных на систематические погрешности приборов, принимаются равными 0 2н — 0 5 цены наименьшего деления шкалы, если эта величина не превышает вариации показаний прибора. В противном случае максимальная абсолютная погрешность равна вариации показа ний прибора, которая определяется при тарировании.
 

Максимальные абсолютные погрешности показаний манометров М и Мв, исправленных на систематические погрешности приборов, принимаются равными 0 2 — 0 5 цены наименьшего деления шкалы, если эта величина не превышает вариации показаний прибора. В ином случае максимальная абсолютная погрешность будет равна вариации показаний прибора, которая определяется при тарировании.
 

Вид кривой У 10 — 4Х2 и ее аппроксимация линейными отрезками.

Точность результата зависит от того, в каком состоянии находится счетчик-интегратор в момент остановки цикла вычисления. Для этого значения получаем максимальную абсолютную погрешность — 5 импульсов младшего разряда.
 

Например, при отсчете или установке визира на логарифмической линейке длиной 250 мм ошибка не превышает 0 1 мм. Таким образом, обычно бывает известна максимальная абсолютная погрешность, получаемая при измерении величины х; обозначим эту погрешность через их.
 

Абсолютная и относительная погрешности

Абсолютная погрешность величины — это разница между ней и принятым точным значением. Чтобы определить этот показатель, из большего числа вычитают меньшее. Единицы обозначения такие же, как и для основной величины. В формулах обозначается греческой буквой дельта и исследуемой величиной.

Пример: В пакете находится 478 граммов сахара. Это число можно округлить до 500. В этом случае абсолютная погрешность приближения будет 500 — 478 =22 г

Для вычислений разработана специальная формула: Δа=А-а,

где А — это точная величина,

а — приближенная, это число, которое немного отличается от точного.

Результаты вычисления записывают со знаком ±. Например, длина бумажного рулона составляет 25 м ± 5 см. Наибольшее значение абсолютной погрешности принято называть ее пределом.

Чтобы получить измерения высокой точности, рассчитать абсолютную погрешность недостаточно. Если измерять предмет длиной 30 см и допустить неточность в 1 см, ее величина будет значительной. При измерении 30-метрового участка дороги то же самое отклонение в 1 см допускается, такое измерение будет наиболее точным. При вычислении ускорения свободного падения с помощью маятника неточность не превышает 10 -5 м/с. 2

Относительная погрешность — условная величина, равная отношению абсолютной к самому числу.

Пример: количество сахара в пакете равно 478 граммов, абсолютная погрешность составляет 22 грамма, относительная равняется 22: 478 = 0, 046. Если перевести в проценты, получается 4,6%. Для отрезка длиной 10 см погрешность в 1 см будет составлять 10%, а для отрезка в 1 м такая же абсолютная величина составит всего 1%. Относительная оценка считается наиболее точной.

Относительная погрешность может быть случайной, возникающей под действием внешних факторов. Ее размер зависит от способа нахождения.