Задачи на движение

Коэффициент использования пробега (КИПр)

Определяет степень использования пробега автомобиля с грузом.

При работе автомобиля на линии различают пробеги: общий, с грузом, холостой и нулевой.

Общий пробег — это расстояние в километрах, проходимое автомобилем в течение рабочего дня.

Пробег с грузом является производительным пробегом.

Холостой пробег — это пробег автомобиля без груза между пунктами разгрузки и погрузки. Нулевой пробег — это пробег автомобиля от парка до пункта погрузки и с последнего пункта разгрузки до парка, а также проезды на заправку топливом. Коэффициент использования пробега определяют по формуле:

где: S_гp — пробег с грузом, км; S_о.пр — общий пробег автомобиля, км.

Пример. Общий пробег автомобиля за день составил 320 км, с грузом — 244 км. Определить КИПр.

Решение.

Величина коэффициента использования пробега зависит от размещения пунктов погрузки и разгрузки, характера грузопотоков и организации диспетчерской службы на линии. Водители-новаторы добиваются сокращения непроизводительных пробегов за счет перевозки попутных грузов. Например, при перевозке сахарной свеклы с поля на сахарный завод они используют обратные рейсы для перевозки на поля минеральных удобрений.

Решение задач на среднюю скорость

Решение задач на среднюю скорость

Задачи простые, важно понять и запомнить формулу:

Если участков пути было два, тогда

Если три, то соответственно:

Как вы поняли, смысл таков: в знаменателе складываются отрезки времени, в

числители суммируем расстояния пройденные за соответствующие им отрезки

№1: Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 61

км/ч, а вторую половину времени – со скоростью 87 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения.

В задаче сказано о двух участках пути.

Среднюю скорость будем искать по формуле:

Пусть на весь путь автомобиль затратил t часов.

Значит за первую половину времени со скоростью 61 км/ч автомобиль прошёл

0,5∙t∙61 километров, а за вторую половину времени 0,5∙t∙87 километров, тогда:

№2: Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74

км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

№3: Путешественник переплыл море на яхте со средней скоростью 17 км/ч.

Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите

среднюю скорость путешественника на протяжении всего пути. Ответ дайте в

Мы не знаем, каким было расстояние, которое преодолел путешественник. Знаем

только, что это расстояние было одинаковым на пути туда и обратно.

Когда расстояние не указано его принимают за 1 (в данном случае — одно море).

Тогда время, которое путешественник плыл на яхте, равно 1/17, а время, затраченное

на полет, равно 1/323.

Общее время равно:

Тогда средняя скорость равна:

Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он

летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость

путешественника на протяжении всего пути. Ответ дайте в км/ч.

№5: Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть –

со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения. В

задаче сказано о трёх участках пути.

Среднюю скорость будем искать по формуле:

Обозначим весь пусть S.

Тогда первую треть пути автомобиль ехал:

Вторую треть пути автомобиль ехал:

Последнюю треть пути автомобиль ехал:

№6: Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть –

со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

№7: Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со

скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения. В

задаче сказано о трёх участках пути.

Среднюю скорость будем искать по формуле:

Исходя из условия мы можем определить протяжённость каждого участка:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

№8: Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со

скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

№9: Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км — со

скоростью 80 км/ч, а затем 150 км — со скоростью 100 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения. В

задаче сказано о трёх участках пути.

Среднюю скорость будем искать по формуле:

Протяжённость участков дана. Определим время, которое затратил автомобиль на

каждый участок: на первый участок автомобиль затратил 120/60 часов, на второй

участок 120/80 часов, на третий 150/100 часов.

Находим среднюю скорость:

№10: Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со

скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю

Курс повышения квалификации

Сейчас обучается 807 человек из 76 регионов

Курс профессиональной переподготовки

Сейчас обучается 358 человек из 68 регионов

Курс повышения квалификации

Современные педтехнологии в деятельности учителя

• Курс добавлен 23.09.2021
• Сейчас обучается 46 человек из 23 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-309466

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Как решать задачи на среднюю скорость

В ЕГЭ по матматике профильного уровня встречаются задачи на нахождение средней скорости автомобиля, путешественника, бегуна и т.п. В этой статье мы постараемся разобраться со способами решения данного типа зданий. Попробуйте решить следующие задачи:

1. Первую треть трассы велосипедист ехал со скоростью 12 км/ч, вторую треть – со скоростью 16 км/ч, а последнюю треть – со скоростью 24 км/ч. Найдите среднюю скорость велосипедиста на протяжении всего пути. Ответ дайте в км/ч.
2. Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость путешественника на протяжении всего пути. Ответ дайте в км/ч.
3. Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74 км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Если у Вас возникает недопонимание, или же вы просто не знаете как решать такие задачи, то данная статья предназначена как раз для Вас!

Средняя скорость объекта

Для начала вспомним формулу, по которой решаются все задачи на движение: ​ \( S=vt \) ​ — пройденный путь равняется произведению скорости и времени. Так вот, средняя скорость равна отношению всего пути ко времени, которое было затрачено на прохождение этого пути. Если перевести на математический язык:

Однако, раз возникла нужда вычислить среднюю скорость, то наверняка она была разной на различных промежутках. Например, Вам необходимо прийти в школу. Сначала вы какой-то путь проезжаете на автобусе, а затем идете пешком. Условно, весь ваш путь можно разделить на 2 промежутка, и на обоих Ваша скорость и время его прохождения будет разной. Поэтому, если в задаче дано несколько промежутков, то мы должны найти общий путь, который равен сумме всех промежутков вашего пути (то есть ​ \( S=S_1+S_2+\ldots+S_n \) ​ (где ​ \( n \) ​ — количество путей, на которых скорость была постоянной). Аналогично мы должны вычислить и общее время, которое было затрачено на прохождение всего пути. То есть ​ \( t=t_1+t_2+\ldots+t_n \) ​, причем время вычисляем на каждом промежутке! То есть, запишем математически формулу для нахождения времени на n-м промежутке: ​ \( t_n=\dfrac\) ​

Решение задач

А теперь, обогатившись некоторой теорией решим первую из предложенных задач:

Решение:

1. По условию задачи мы видим, что автомобиль прошёл сначала одну треть, затем вторую треть и последнюю треть. Значит весь его маршрут состоит из трёх участков. Поэтому удобно обозначить длину всего его пути за ​ \( 3S \) ​
2. Теперь нам необходимо выяснить за какое время автомобиль прошёл каждый из этих промежутков (воспользовавшись формулой ​ \( t_n=S_n/v_n \) ​). Причем длина каждого из трёх промежутков будет равна S.
   1. Время, за который был пройдена первая треть: ​ \( t_1=\dfrac\) ​.
   2. Аналогично, найдем время, за которое были пройдены вторая и третья трети всего пути: ​ \( t_2=\dfrac\) ​ и ​ \( t_3=\dfrac\) ​
3. Итак, мы выяснили сколько времени тратит автомобиль на прохождение каждого из отрезков своего пути, значит можем найти сколько он потратил времени всего: ​ \( t=t_1+t_2+t_3 \) ​. Таким образом: ​ \( t=\dfrac\) ​

Теперь мы знаем длину всего пути ( \( 3S \) ​) и сколько времени автомобиль затратил на прохождение всего пути ( \( t=\dfrac \) ​, значит найти среднюю скорость не составит и труда:

Теперь постарайтесь самостоятельно решить оставшиеся две текстовые задачи на нахождение средней скорости, а если не получается, то посмотрите видео-урок

Видео-урок: “Как решать задачу на нахождение средней скорости”:

В данном видео-уроке я покажу, как решаются все три предложенные текстовые задачи на нахождение средней скорости. Также Вы можете сравнить своё решение с моим.

Равноускоренное движение

Если в течение времени положение тела изменяется относительно предметов, находящихся в покое, то считается, что оно движется. При этом в качестве основного параметра, описывающего перемещение, используется скорость. Движение тела или точки можно представить в виде линии, повторяющей путь прохождения. Называется она траекторией. Если линия прямая, то движение считается прямолинейным.

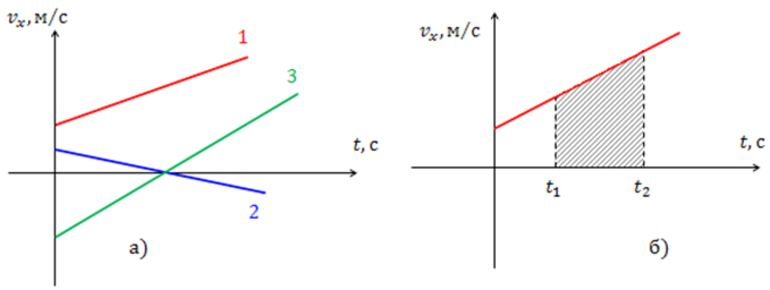
Неравномерное движение характеризуется перемещением по различной траектории с непостоянной величиной скорости. При этом изменение положения может быть равноускоренным, то есть параметр на одинаковых промежутках увеличивается или уменьшается на одно и то же значение. В качестве примера можно привести падение камня.

Таким образом, если векторы V и ускорения A лежат вдоль прямой, то в проекциях такое направление можно рассматривать как алгебраические величины. При равноускоренном движении по прямой траектории скорость точки вычисляется по формуле: V = V0 + A*t. Где:

• V0 — начальная скорость;
• A — ускорение (имеет постоянное значение);
• t — время движения.

Это основная формула в физике. На графике она изображается как прямая линия v (t). По оси ординат откладывается время, а абсцисс — скорость. Построив график, по наклону прямой можно определить ускорение точки A. Для этого используется формула нахождения сторон треугольника: A = (v-v0) / t.

Если на оси времени выделить промежуток Δt, то можно предположить, что движение будет равномерным и описываться некоторым параметром, равным мгновенному значению в середине отрезка. Эта моментальная величина является векторной. Она численно равна пределу, который пытается достигнуть скорость за промежуток времени, стремящийся к нулю. В физике это состояние описывается формулой мгновенной скорости: V = lim (Δ s/ Δ t) = r-1(t). То есть, с математической точки зрения, это первая производная.

Из этой формулы можно вывести выражение для нахождения конечной скорости материальной точки: V = (V20 — 2* A * s)½. Если же в начальный момент V0 = 0, то формулу можно упростить до вида: V = (2* A * s)½.

Основные понятия и законы кинематики

кинематикойМеханическим движениемСистемой отсчётаТелом отсчётаМатериальной точкойТраекториейпрямолинейноекриволинейноеПуть — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).

Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение — это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории

А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории.

Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещенияСкоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:

Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:

Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину

Ускорением

Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x + V_xt, где x — начальная координата тела, V_x — скорость движения.Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с2, не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.

Скорость при свободном падении рассчитывается по формуле:
Перемещение по вертикали рассчитывается по формуле:

Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости
ω:
Угловая скорость связана с линейной скоростью соотношением где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν
Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности:

Как найти скорость, формула

Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.

Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики.

Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.

1

Как найти скорость – равномерное движение

Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.

Тогда V=S/t, где:

• V – искомая скорость,
• S – пройденное расстояние (общий путь),
• t – общее время движения.

2

Как найти скорость – ускорение постоянно

Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:

V=V (нач) + at, где:

• V (нач) – первоначальная скорость движения объекта,
• a – ускорение тела,
• t – общее время пути.

3

Как найти скорость – неравномерное движение

В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),

S(2) – за t(2) и т.д.

На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.

Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:

V= (S(1)+S(2))/(t(1)+t(2)).

В случае вращения речь идет об угловой скорости, определяющей угол, на который поворачивается элемент за единицу времени. Обозначается искомая величина символом ω (рад/с).

Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).

В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:

• ω = 2π/T, где:
  π – константа ≈3,14,
• T – период.
• Или ω = 2πn, где:
  π – константа ≈3,14,
• n – частота обращения.

При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:

1. ω = V/R, где:
   V – численное значение векторной величины (линейной скорости),
2. R – радиус траектории следования тела.

5

Как найти скорость – сближение и отдаление точек

• В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.
• Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
  V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.
• Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).

6

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

Средняя скорость — движение — автомобиль

Средняя скорость движения автомобиля зависит от максимальной скорости, которую он может развить на дорогах различного качества, и от интенсивности разгона. Кроме того, на среднюю скорость автомобиля существенное влияние оказывают его тормозные свойства.
 

Средние скорости движения автомобилей приведены для дорог с усовершенствованным типом покрытия в хорошем состоянии.
 

Средняя скорость движения автомобиля составляет v км / час.
 

Средняя скорость движения автомобиля зависит от многих факторов: на нее влияют, с одной стороны, конструктивные особенности автомобиля, а с другой — дорожные условия. При испытаниях ее стремятся поддерживать максимально возможной. Чтобы полнее выяснить причины, вызывающие ограничение скорости, принято определять среднюю скорость чистого движения и среднюю техническую скорость.
 

Стремление повысить среднюю скорость движения автомобилей ( автопоездов) при одновременном увеличении их полной массы приводит к повышению мощности двигателя, что, в свою очередь, вызывает повышенные требования к трансмиссии автомобиля. Это непосредственно относится и к ведущему мосту, назначение которого состоит в изменении крутящего момента двигателя при передаче его к ведущим колесам таким образом, чтобы вместе с коробкой передач обеспечить согласование скоростной характеристики двигателя с динамической характеристикой автомобиля.
 

График, для определения нагрузочного режима трансмиссии автомобиля ( по нормали.

Угловую скорость рассчитываемых подшипников определяют по средней скорости движения автомобиля аа ср — с учетом соответствующего передаточного числа между валами коробки передач.
 

Эффективность действия тормозов оказывает влияние на среднюю скорость движения автомобиля, особенно в условиях городского движения.
 

Именно эта скорость имеется в виду, когда, например, говорят о средней скорости движения автомобиля или средней скорости поезда.
 

За эквивалентное число оборотов пэкв принимается число оборотов подшипника ( вала), соответствующее средней скорости движения автомобиля на основной ( прямой) передаче.
 

Установка на шасси автомобиля двигателя повышенной мощности, ранее практиковавшаяся в Америке, повышала среднюю скорость движения автомобиля, уменьшала его износы и шумность работы, но ухудшала топливную экономичность. Последнее объясняется тем, что в двигателях большей мощности и большого рабочего объема при работе на малых нагрузках возрастает относительная величина тепловых, насосных и механических потерь.
 

Расстояние между площадками для кратковременных остановок и стоянок автомобилей зависит от интенсивности движения на дороге, средней скорости движения автомобилей, вместимости стоянки и средней продолжительности пребывания автомобиля на стоянке.
 

Зависимость коэффициента сцепления от различных факторов.

В практике управления автомобилем важно знать н только максимальную скорость движения автомобиля на отдельных участках маршрута, но и среднюю скорость на всем маршруте. Возможность определения средней скорости движения автомобиля имеет практическое значение для осуществления планирования перевозок грузов и пассажиров на автомобильном транспорте.
 . Из выражения ( 34) следует, что чем выше удельная мощность, тем больше ускорение разгона и меньше продолжительность этапа разгона до установившейся скорости

Из выражения ( 34) следует, что чем выше удельная мощность, тем больше ускорение разгона и меньше продолжительность этапа разгона до установившейся скорости

В итоге следует ожидать повышения средней скорости движения автомобиля. Для того чтобы оценить степень влияния удельной мощности на среднюю скорость вследствие сокращения именно этого этапа цикла, рассмотрим процесс разгона автомобиля с учетом переключения передач.
 

Из выражения ( 34) следует, что чем выше удельная мощность, тем больше ускорение разгона и меньше продолжительность этапа разгона до установившейся скорости. В итоге следует ожидать повышения средней скорости движения автомобиля. Для того чтобы оценить степень влияния удельной мощности на среднюю скорость вследствие сокращения именно этого этапа цикла, рассмотрим процесс разгона автомобиля с учетом переключения передач.
 

Задача №6

Самолет, летящий со скоростью $300 \frac$, в безветренную погоду пролетел расстояние между аэродромами A и B за $2.2 \space ч$. Обратный полет из-за встречного ветра он совершил за $2.5 \space ч$. Определите скорость ветра.

Дано:$\upsilon_1 = 300 \frac$$t_1 = 2.2 \space ч$$t_2 = 2.5 \space ч$

Показать решение и ответ

Решение:

Сначала вычислим расстояние между аэродромами, которое пролетает самолет:$S = \upsilon_1 t_1$,$S = 300 \frac \cdot 2.2 \space ч = 660 \space км$.

Теперь рассчитаем скорость, с которой самолет совершил обратный полет:$\upsilon_2 = \frac$,$\upsilon_2 = \frac = 264 \frac$

Если бы ветра не было, то скорость самолета составила бы $300 \frac$. Но ветер направлен противоположно движению самолеты, вектор его скорости противоположно направлен вектору скорости самолета. Поэтому мы можем записать, что скорость самолета, летящего при встречном ветре, равна разности скорости самолета в безветренной обстановке и скорости ветра:$\upsilon_2 = \upsilon_1 — \upsilon_в$.

Рассчитаем скорость ветра:$\upsilon_в = \upsilon_1 — \upsilon_2$,$\upsilon_в = 300 \frac — 264 \frac = 36 \frac$,или в СИ $\upsilon_в = 36 \cdot \frac = 10 \frac$.

Ответ: $\upsilon_в = 10 \frac$.