Простые механизмы
Содержание:
Содержание
Слайд 1
Подготовила: учитель физики МБОУСОШ №8 г.Ессентуки Ягодкина Юлия Сергеевна
Слайд 2
Простые механизмы — устройства (приспособления), позволяющие преобразовать силу в силу, существенно большую.
Простые механизмы
Рычаг Наклонная плоскость (блок, ворот, лом) (клин, винт)
Простые механизмы дают выигрыш в силе.
Слайд 3
Рычаг – твёрдое тело, которое может вращаться вокруг неподвижной опоры.
Рычаг начал применяться людьми ещё в глубокой древности. С его помощью удавалось поднимать тяжёлые каменные плиты при постройке пирамид в Древнем Египте.
Слайд 4
F₁ ⁄ F₂ = ℓ₂/ ℓ₁
Слайд 5
Физическая величина, равная произведению силы на её плечо, называется моментом силы.
M₁=M₂
Рычаг находится в равновесии, если момент силы, вращающий его по часовой стрелке равен моменту силы, вращающей его против часовой стрелке.
Слайд 6
Слайд 7
Различные части тела животного и человека, например конечности, могут действовать как рычаг.
Рычаги передней конечности собаки
Одноплечный рычаг руки человека
Слайд 8
Блок– это колесо с желобом, по которому пропускают верёвку, трос или цепь.
Блок подвижный неподвижный
Даёт выигрыш в силе в 2 раза.
Слайд 9
Обычно на практике применяют комбинацию подвижного блока с неподвижным.
Неподвижный блок не даёт выигрыша в силе. А применяется для удобства. Он изменяет направление действия силы, например, позволяет поднимать груз, стоя на земле.
Слайд 10
Для получения большего выигрыша в силе применяют грузоподъёмный механизм – полиспаст.
Слайд 11
Наклонная плоскость— простой механизм в виде плоской поверхности, установленной под углом, отличным от прямого, к горизонтальной поверхности.
Слайд 12
Клин — простой механизм в виде призмы, рабочие поверхности которого сходятся под острым углом. Используется для раздвижения, разделения на части обрабатываемого предмета.
Слайд 13
Винт — простой механизм. Резьба винта, в сущности, представляет собой другой простейший механизм — наклонную плоскость, многократно обёрнутую вокруг цилиндра.
Слайд 14
Ворот- это два колеса, соединенные вместе и вращающиеся вокруг одной оси, например, колодезный ворот с ручкой.
Слайд 15
Лебедка — конструкция , состоящая из двух воротов с промежуточными передачами в механизме привода.
Слайд 16
Архимед (287-212 г.г
до н.э.)
Баллиста
Катапульта
Слайд 17
Во сколько раз выигрываем в силе, во столько же раз проигрываем в расстоянии.
Слайд 18
Слайд 19
Домашнее задание.
А.В.Пёрышкин Физика-7 §55-60.
Слайд 20
Спасибо за внимание!
Посмотреть все слайды
КПД – коэффициент полезного действия
Прежде нужно разобраться в словах «полезное действие». Вот пример. Картофель, собранный для хранения на семена, фермер засыпает из ведер в большие контейнеры. Погрузка картофеля ведрами является полной (иначе совершенной) работой. Она состоит из подъема ведер и самого картофеля. Подъем картофеля – это работа полезная, а заполнение и поднятие ведер – бесполезная. Ведра нужно поднимать, опускать, наполнять картофелем.
Полная работа, конечно же, превышает полезную. Находя, как относится полезная работа к полной (совершенной работе), получают величину, называемую коэффициентом полезного действия (КПД). Часто КПД вычисляется в процентах. Для обозначения используется буква η (эта) из греческого алфавита.
η = (Аполезная/Аполная) ∙ 100 %
КПД можно рассчитать следующим образом. Пусть дана наклонная плоскость:
Схематически на рисунке это выглядит так:

Работая над конструкциями и создавая машины, изобретатели стараются повысить КПД. Уменьшая массу работающих и движущихся частей в устройствах, трение контактирующих деталей, конструкторы добиваются неплохих результатов.
Нужно отметить, что нет механизмов, дающих КПД в 100%. В настоящее время уже есть машины и механизмы с КПД около 98-99 %, но создать работающее устройство со 100% — м КПД невозможно.
Словарь
1. Тычинка – мужская составляющая в строении цветка. Содержит пыльник с пыльцой, тычиночную нить.
2. Пыльник – часть тычинки, где созревает пыльца.
3. Пестик – часть цветка, представляющая женский орган с рыльцем, столбиком и завязью.
4. Призма – физическое тело, многогранник с двумя параллельными основаниями и боковыми гранями – параллелограммами. (Клин – треугольная призма, в основаниях которой лежат треугольники).
Для чего нужны простые машины?
Простые машины облегчают работу, выполняя одну или несколько из следующих функций:
— Перенести силы из одного места в другое.
— Измените направление силы.
— Увеличьте величину силы.
— Увеличьте дистанцию силы.
Хотя простые машины имеют множество различных форм, они бывают шести основных типов:
— Клин: устройство для разделения вещей.
— Колесо и ось: используются для уменьшения трения и как усилитель.
— Рычаг: перемещается вокруг точки опоры для увеличения или уменьшения механического преимущества.
— Наклонная плоскость: поднимайте предметы при подъеме по склону.
— Винт: устройство, которое может поднимать или удерживать предметы вместе.
— Шкив: изменяет направление силы.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Исследуя условия равновесия рычага, ученик выполнил соответствующую лабораторную работу. В таблице представлены значения сил и их плеч для рычага, находящегося в равновесии. Определите, чему равно плечо \( l_1 \)?

1) 12,8 м
2) 2,5 м
3) 0,8 м
4) 0,25 м
2. Ученик выполнял лабораторную работу по исследованию условий равновесия рычага. Результаты для сил и их плеч, которые он получил, представлены в таблице.

Чему равна сила \( F_1 \), если рычаг находится в равновесии?
1) 100 Н
2) 50 Н
3) 25 Н
4) 9 Н
3. Рычаг находится в равновесии под действием двух сил. Сила \( F_1 \) = 6 Н. Чему равна сила \( F_2 \), если длина рычага 50 см, а плечо силы \( F_1 \) равно 30 см?
1) 0,1 Н
2) 3,6 Н
3) 9 Н
4) 12 Н
4. Выигрыш в силе, приложенной к грузу, нельзя получить с помощью
1) подвижного блока
2) неподвижного блока
3) рычага
4) наклонной плоскости
5. С помощью неподвижного блока в отсутствие трения силе
1) выигрывают в 2 раза
2) не выигрывают, но и не проигрывают
3) проигрывают в 2 раза
4) возможен и выигрыш, и проигрыш
6. С помощью подвижного блока в отсутствие трения
1) выигрывают в работе в 2 раза
2) проигрывают в силе в 2 раза
3) не выигрывают в силе
4) выигрывают в силе в 2 раза
7. На рисунке изображён неподвижный блок, с помощью которого, прикладывая к свободному концу нити силу 20 Н, равномерно поднимают груз. Если трением пренебречь, то масса поднимаемого груза равна
1) 4 кг
2) 2 кг
3) 0,5 кг
4) 1 кг
8. Наклонная плоскость даёт выигрыш в силе в 2 раза. В работе при отсутствии силы трения эта плоскость
1) даёт выигрыш в 2 раза
2) даёт выигрыш в 4 раза
3) не даёт ни выигрыша, ни проигрыша
4) даёт проигрыш в 2 раза
9. Вдоль наклонной плоскости длиной 5 м поднимают груз массой 40 кг, прикладывая силу 160 Н. Чему равна высота наклонной плоскости, если трение при движении груза пренебрежимо мало?
1) 1,25 м
2) 2 м
3) 12,5 м
4) 20 м
10. Груз массой 10 кг поднимают по наклонной плоскости длиной 2 м и высотой 0,5 м, прикладывая силу 40 Н. Чему равен КПД наклонной плоскости?
1) 160%
2) 62,5%
3) 16%
4) 6,25%
11. Груз поднимают с помощью подвижного блока радиусом \( R \) (см. рисунок). Установите соответствие между физическими величинами (левый столбец) и формулами, по которым они определяются (правый столбец).
Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) плечо силы \( \vec{F}_1 \) относительно точки A
Б) плечо силы \( \vec{F}_2 \) относительно точки A
B) момент силы \( \vec{F}_1 \) относительно точки A
ФОРМУЛЫ
1) \( F_1R \)
2) \( 2F_1R \)
3) \( \frac{F_1}{R} \)
4) \( R \)
5) \( 2R \)
12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.
1) Любой простой механизм даёт выигрыш в силе.
2) Ни один простой механизм не даёт выигрыша в работе.
3) Наклонная плоскость выигрыша в силе не даёт.
4) Коэффициент полезного действия показывает, какая часть совершенной работы является полезной.
5) Неподвижный блок даёт выигрыш в силе в 2 раза.
Часть 2
13. Чему равна сила, с которой действуют на брусок массой 0,2 кг, перемещая его по наклонной плоскости длиной 1,6 м и высотой 0,4 м, если КПД наклонной плоскости 80%.
Простейшие механизмы
Для облегчения совершения механической работы издавна используются различные приспособления — простые механизмы.
Простые механизмы — это устройства, в которых работа совершается только за счет механической энергии. Простые механизмы (рычаг, наклонная плоскость, блок и др.) служат для преобразования силы, их применяют при совершении работы в тех случаях, когда надо действием одной силы уравновесить другую силу.
Наклонная плоскость
Ее используют в тех случаях, когда надо поднять тяжелый груз на некоторую высоту.
Рассмотрим гладкую наклонную плоскость (рис. 1). Рассчитаем силу F, которую надо приложить к телу массой m, чтобы поднять его равномерно на высоту h.
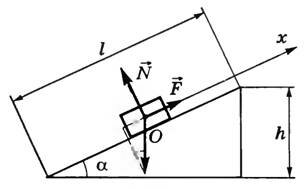
Рис. 1
Запишем основное уравнение динамики\. Спроецируем это равенство на ось Ox\. Отсюда искомая сила
\(~F = mg \sin \alpha = mg \frac hl \Rightarrow \frac{mg}{F} = \frac lh,\)
т.е для равномерного поднятия груза с помощью наклонной плоскости необходимо приложить силу, во столько раз меньшую силы тяжести груза, во сколько раз длина наклонной плоскости больше ее высоты.
Рычаг
Рычагом называют имеющее неподвижную ось вращения твердое тело, на которое действуют силы, стремящиеся повернуть его вокруг этой оси. Различают рычаги первого и второго рода.
Рычагом первого рода называют рычаг, ось вращения О которого расположена между точками А и В приложения сил, а сами силы направлены в одну сторону (рис. 2, а). Это коромысло равноплечих весов, железнодорожный шлагбаум, ножницы и др.
Рис. 2
Рычаг второго рода — рычаг, ось вращения О которого расположена по одну сторону от точек приложения сил, а сами силы направлены противоположно друг другу (рис. 2, б). Это гаечные ключи, щипцы для раскалывания орехов, двери и др.
Условие равновесия рычага вытекает из M1 = M2.
Так как M1 = F1l1 и M2 = F2l2, где l1 и l2 — плечи сил, действующих на рычаг, то \(~\frac{F_1}{F_2} = \frac{l_2}{l_1}\) — условие равновесия рычага.
При равновесии рычага под действием двух сил модули этих сил обратно пропорциональны их плечам.
С помощью рычага можно получить выигрыш в силе, т.е. меньшей силой можно уравновесить большую силу.
Блок
Блоки используют для поднятия грузов. Блок представляет собой колесо с желобом, укрепленное в обойме. По желобу блока пропускают веревку, трос или цепь. Неподвижным называют такой блок, ось которого закреплена и при подъеме грузов она не поднимается и не опускается (рис. 3, а, б).
Рис. 3
Неподвижный блок можно рассматривать как равноплечий рычаг, у которого плечи приложенных сил равны радиусу колеса. Следовательно, из правила моментов mgr = Fr вытекает, что неподвижный блок выигрыша в силе не дает (F = mg). Он позволяет менять направление действия силы.
Рис. 4
На рисунке 4, а, б изображен подвижный блок (ось блока поднимается и опускается вместе с грузом). Такой блок поворачивается около мгновенной оси О. Правило моментов для него будет иметь вид
\(~mgr = F \cdot 2r \Rightarrow F = \frac{mg}{2}.\)
Таким образом, подвижный блок дает выигрыш в силе в два раза.
Обычно на практике применяют комбинацию неподвижного блока с подвижным (рис. 5). Неподвижный блок применяется только для удобства. Он, изменяя направление действия силы, позволяет, например, поднимать груз, стоя на земле.
Рис. 5
Перечень неисправностей КШМ
Главные неприятности, которые могут случится с кривошипно-шатунным механизмом:
- Как шатунные, так и коренные шейки коленчатого вала подвержены износу и механическим повреждениям.
- Износ, механические повреждения и даже расплавление могут угрожать и вкладышам (подшипникам) шеек коленвала.
- «Болезни» поршневых колец – это закоксовывание не до конца сгоревшими продуктами горения (углеводороды окисляются только до углерода), их залегание и даже поломки, что может привести к фатальным последствиям.
- Цилиндропоршневая группа также подвержена износу. В современных «движках» это не так заметно, всё-таки они созданы по последнему слову техники, но у каждой детали имеется конечный ресурс.
- На днище поршня может отложиться нагар.
- В деталях могут появиться трещины, они могут прогореть, обломиться и даже расплавиться.
- Двигатель может даже заклинить.
Требования безопасности
При проектировании и монтаже рычажного механизма учитываются требований безопасности. Они во многом зависят от области применения устройства, а также особенностей самого механизма.

Среди особенностей этого момента можно отметить следующее:
- При изготовлении должен подбираться материал, который будет соответствовать всем требованиям. Примером можно назвать высокую коррозионную стойкость. При проектировании указывается то, какой именно материал должен применяться при изготовлении устройства. Часто отдается предпочтение углеродистой стали и легированным сплавам. Некоторые элементы могут быть изготовлены из уплотнительных и других материалов, все зависит то конкретного случая.
- При проектировании учитывается то, каким образом происходит перераспределение нагрузки. Это связано с тем, что в некоторых местах она будет критической.
- Под активным элементом при подъеме тяжелых объектов не должно находится людей, другого оборудования, а также частей самого рычажного механизма. Это связано с высокой вероятностью падения переносимого груза.
- Перед непосредственным применением оборудования следует проводить визуальный осмотр, который позволяет определить наличие или отсутствие повреждений. Кроме этого, должно проводится периодическое обслуживание. Даже незначительный дефект может стать причиной существенного снижения прочности рычажного механизма. Периодическое обслуживание позволяет существенно продлить срок службы устройства.
- Запрещается применять механизм не по предназначению. Перед каждым его использованием проверяется надежность крепления. Нагрузка должна оказываться на конструкцию соответствующим образом, так как в противном случае происходит неправильное перераспределение силы. Именно поэтому при проектировании указывается то, каким образом устройство должно устанавливаться и как использоваться.
- При применении учитывается то, на какую максимальную нагрузку рассчитано оборудование. Слишком высокий показатель может стать причиной, по которой происходит повреждение основных элементов. При проектировании учитывается то, какая нагрузка может оказываться на конструкцию.
Как правило, соответствующее руководство по применению устройства составляется непосредственно на месте его эксплуатации в соответствии с установленными нормами. Это связано с тем, что рычажные механизмы получили весьма широкое распространение, могут устанавливаться в качестве составного узла другого оборудования.
При этом узел оборудован тремя важными независимыми системами:
- Гидравлическая. Эта часть устанавливается в большинстве случаев для передачи усилия. Гидравлика получила весьма широкое распространение, так как она предназначена для непосредственной передачи усилия. Гидравлическая часть основана на подаче специальной жидкости, при помощи которой проводится передача усилия. Гидравлика несет с собой опасность по причине того, что подвижный элементы могут передавать усилие. Поэтому все основные элементы должны быть защищены от воздействия окружающей среды, для чего проводится установка различных кожухов.
- Механическая. Механика отвечает за непосредственную передачу усилия и достижения других целей. Неправильная работа устройства может стать причиной повреждения и деформации. Механика также защищается специальными кожухами, так как попадание посторонних элементов запрещается.
- Электрическая. Для управления механизмом проводится установка электрической части. Она должна быть защищена от воздействия окружающей среды, так как даже незначительное механическое воздействие может стать причиной повреждения магистрали электроснабжения.
Опасность с собой несет и электрическая часть, которая состоит из конечных выключателей. Схема подключения предусматривает использование как минимум двух выключателей, устройство должно обесточиваться в случае выхода из строя одного из них.
Механическая система защиты действует путем прерывания подачи масла в гидравлический цилиндр. При этом проводится слив масла с цилиндра в общую емкость. Подобная система срабатывает даже при незначительном повреждении устройства.
Определение и разновидности
Из уроков истории известны факты применения приспособлений для метания снарядов, перемещения строительных материалов, передачи механической энергии. Они вызывали движения, преодолевающие большие силы, особенно противодействующие им в начале процесса, например, сдвигание тяжелого камня с места. Из предыдущих уроков вы знаете, что такое механическая работа. Она вычисляется как произведение приложенной к телу силы на преодолённое под её действием расстояние: A = F*s.
Природа создана так, что в замкнутой системе получить выигрыш в работе нельзя. Во сколько раз меньшую силу приложите, во столько проиграете в расстоянии – тело придётся перемещать дальше и наоборот. Простые механизмы применяют для того, чтобы развивать силы, равные по модулю и противоположные по значению противодействующим движению силам.
При расчётах величиной сил трения могут пренебрегать.
Замена цилиндра замка
Цилиндровый замок врезной с защёлкой удобен тем, что при необходимости не обязательно демонтировать всё устройство – достаточно заменить личинку. Провести замену цилиндра замка можно самостоятельно следуя предложенному алгоритму:
- Открыть дверь, в торце найти на планке винт возле цилиндра.
- Выкрутить винт.
- Если замки с ручками – цилиндр легко достаётся, если без – необходимо вставить ключ в разъём, повернуть против часовой стрелки до упора и потянуть на себя.
- Затем ключ и ручку чуть передвинуть в противоположную сторону, чтобы рычаг опустился вниз – тогда цилиндр легко выйдет из корпуса.
- Новый цилиндр помешается в механизм за ручку, или вставленным в него ключом. Следить за положением рычага – он должен полностью быть в секрете.
- Попробовать закрыть врезной замок с защёлкой, передвигая верёд и назад, что бы он свободно закрывался.
- Установить на место винт.
- Проверить работу.

Чтобы заменить личинку накладного замка, корпус необходимо снять с полотна. Затем всё как с предыдущим – найти винт, достать старый цилиндр и заменить новым механизмом.
Чтобы не прогадать с размером цилиндра рекомендуется совершать покупку нового со старым механизмом или измерить его размер.
Момент силы. Простые механизмы в природе, технике и быту
Из пропорции F2/F1 = l1/l2 получается равенство F1 ∙ l1 = F2∙ l2. Используя его, П.Вариньон (французский ученый) ввел первое определение момента силы:
Момент силы – это одна из величин, полученных путем математических преобразований. Использовали основное свойство пропорции F2/F1 = l1/l2, получили новое равенство F1 ∙ l1 = F2∙ l2. Слева и справа произведения одинаковых физических величин, только индексы разные. Слева — первая сила и ее плечо, справа — вторая сила и ее плечо. Назвали такое произведение моментом силы.
Если к телу приложены две силы, одна поворачивает тело по часовой стрелке, а другая – против, то для соблюдения равновесия нужно равенство:

Правило моментов соблюдается для произвольного жесткого тела, у которого зафиксирована ось вращения. Пусть тело произвольной формы имеет возможность вращаться (на рис. т.О обозначает ось). Плечом силы d здесь выступает расстояние от линии этой силы до оси. На тело может действовать несколько сил (необязательно две).
Из определения момента F ∙ l = M даже незначительная сила может дать большой вращающий момент, если взять достаточно большое плечо. Это условие часто применяют в технических и бытовых ситуациях. Расширенная рукоятка ключей, штопоров и отверток, удлиненные ручки гаечных ключей, вытянутые ручки ножниц по металлу – в этих устройствах длинные плечи.
Во многих отраслях деятельности человек издавна не обходится без использования рычагов. Это – технические устройства, механизмы, строительство.
Природа также создала много примеров рычагов. Самый замечательный из них – человеческая рука.
Чтобы удержать в руке тело, нужно уравновесить силу тяжести F2 и мышечную силу руки F1.
Интересен и такой пример природы. «Рычажный механизм» внутри цветка шалфея «загружает» шмелей пыльцой. Шмель, приземлившись на губу цветка (шалфей – семейство губоцветных), проникает внутрь за нектаром. У входа в цветок находятся две тычинки. Они преграждают путь шмелю. Тычинки по внешнему виду напоминают рычаг. Мелкая часть каждой тычинки представляет одно плечо рычага. Находится это плечо снизу. Другое плечо рычага – это длинная верхняя часть тычинки. На ней раскачивается пыльник.
Шмель, залезая в цветок, давит на нижнее, короткое, плечо. Сверху длинное плечо наклоняется, и пыльник смазывает пыльцой спинку насекомого. А дальше шмель садится на следующий цветок. Спинка зацепляется за рыльце пестика другого цветка. Рыльце легко задеть, так как оно наклонено вниз. Пыльца попадает внутрь пестика. Таким образом происходит опыление шалфея насекомыми.
Простые механизмы: блок и ворот – это виды рычагов.
Ворот — по сути бревно, способное вращаться вместе со своей осью. К оси крепится ручка, держась за которую можно осуществлять вращение. Как простой механизм ворот часто применяют при подъеме тяжелых грузов с глубины.
Чтобы увидеть в блоке рычаг, нужно мысленно диаметрально провести через центр блока отрезок (на рисунке отрезок АВ). Тогда l1 и l2 будут плечами приложенных к тросу сил.
Плечи сил F1 и F2 при равновесии одинаковы, значит и силы тоже одинаковы. Неподвижный блок выиграть в силе не может.
Плечо l1 больше плеча l2 в 2 раза, то есть l1 = 2l2.
Тогда равенство F1 ∙ l1 = F2∙ l2 запишется так: F1 ∙ 2l2 = F2∙ l2 (вместо l1 подставляем 2l2). Слева и справа есть одинаковый множитель l1. на него можно сократить обе части равенства. Получается, что F1 ∙ 2 = F2. Иначе F2 = 2 F1
Из условия равновесия сила F1 меньше силы F2 в 2 раза. Подвижный блок в 2 раза выигрывает в силе.
Часто тяжелые тела поднимают по наклонной плоскости. Работа получается больше, но зато выходит выигрыш в силе. Разделив длину наклонной плоскости на высоту, возможно рассчитать этот выигрыш. В данном случае при условии незначительного трения это будет довольно приближенная оценка.
Привычная лестница – пример наклонной плоскости:
По вертикальной лестнице труднее подниматься. По наклонной лестнице подниматься легче, но она длиннее.
Винты и винтообразные устройства, клинообразные приспособления – часто применяемые разновидности наклонной плоскости. Винт — это накрученная на ось наклонная плоскость. Клин – две наклонные плоскости, объединенные в призму.
 Винт Источник
Винт Источник
 Клин Источник
Клин Источник
Архимедов рычаг
Хорошей помощью в понимании золотого закона механики является презентация работы простого рычага. Он состоит из точки опоры и либо одного, либо двух плеч в зависимости от рода. Существуют три рода этого механизма:
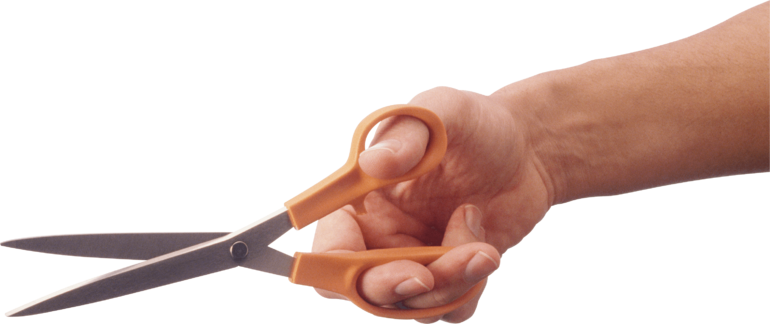
- Точка приложения силы и точка сопротивления ей находятся по разные стороны от опоры. Такая конструкция позволяет с помощью действия меньшей по величине силы противодействовать значительным усилиям, хотя за счет проигрыша в пути. Примерами рычагов первого рода являются ножницы, плоскогубцы, катапульта, действие человеческих суставов и мышц.
- Внешняя сила и сопротивление действуют по одну сторону от опоры так, что плечо сопротивления всегда меньше плеча внешнего усилия. Это расположение действующих сил позволяет всегда выигрывать в силе и проигрывать в перемещении. Примерами механизмов-рычагов второго рода являются одноколесная ручная тачка и орехокол.
- Если внешняя сила и сопротивление приложены по одну сторону от опоры, но первая лежит ближе к ней, чем вторая, то ведут речь о рычаге третьего рода. Смысл его использования заключается в выигрыше. в перемещении, хотя для этого приходится пожертвовать прилагаемым усилием. Здесь можно привести такие примеры, как удочка для рыбной ловли и щипцы для ухода за бровями.
Для рычагов всех родов справедлива следующая формула, которую получил еще Архимед:
F1*d1 = F2*d2.
Произведение силы на длину плеча является величиной постоянной
Следует обратить внимание, что сила должна быть приложена перпендикулярно плечу, если это условие не выполняется, то для справедливости равенства следует в него подставлять не сами силы, а их проекции на перпендикуляры к плечам.. Это выражение показывает равенство моментов
Действительно, согласно определению произведение F*d может рассматриваться как момент силы F. Золотое правило рычага в таком случае преобразуется в следующий вид:
Это выражение показывает равенство моментов. Действительно, согласно определению произведение F*d может рассматриваться как момент силы F. Золотое правило рычага в таком случае преобразуется в следующий вид:
M1 = M2.
Равенство моментов является одним из двух условий равновесия в системах, имеющих оси вращения. Второе условие — это равенство нулю всех действующих в системе сил. В случае рычага, который находится в равновесии, это условие может быть записано так:
F1 + F2 = N.
Где N — сила реакции опоры, вектор которой направлен в противоположную силам действия и противодействия сторону.