«science-pop»

Ежедневные примеры

Легко представить себе изохорный процесс, нужно только думать о процессе, который происходит в постоянном объеме; то есть, в котором контейнер, содержащий вещество или материальную систему, не изменяется в объеме.

Примером может служить случай (идеального) газа, заключенного в закрытый контейнер, объем которого не может быть изменен никакими средствами, к которым подводится тепло. Предположим, в случае газа, заключенного в бутылку.

Передача тепла газу, как уже объяснялось, в конечном итоге приведет к увеличению или увеличению его внутренней энергии..

Обратный процесс будет происходить с газом, заключенным в контейнер, объем которого не может быть изменен. Если газ охлаждается и отдает тепло окружающей среде, тогда давление газа будет уменьшаться, а значение внутренней энергии газа будет уменьшаться..

Идеальный цикл Отто

Цикл Отто является идеальным случаем цикла, используемого бензиновыми двигателями. Тем не менее, его первоначальное использование было в машинах, которые использовали природный газ или другое топливо в газообразном состоянии.

В любом случае идеальный цикл Отто является интересным примером изохорного процесса. Это происходит, когда сгорание смеси бензина и воздуха происходит мгновенно в двигателе внутреннего сгорания..

В этом случае происходит повышение температуры и давления газа внутри цилиндра, при этом объем остается постоянным.

Удельная теплоемкость: понятие и формула для расчета

Формулы количества теплоты для нагревания и охлаждения мы уже разбирали, но давайте еще раз:

Нагревание Q = cm(tконечная — tначальная) Охлаждение Q = cm(tначальная — tконечная) Q — количество теплоты c — удельная теплоемкость вещества [Дж/кг*˚C] m — масса tконечная — конечная температура tначальная — начальная температура

В этих формулах фигурирует такая величина, как удельная теплоемкость. По сути своей — это способность материала получать или отдавать тепло.

С точки зрения математики удельная теплоемкость вещества — это количество теплоты, которое надо к нему подвести, чтобы изменить температуру 1 кг вещества на 1 градус Цельсия:

Удельная теплоемкость вещества c= Q/m(tконечная — tначальная) Q — количество теплоты c — удельная теплоемкость вещества [Дж/кг*˚C] m — масса tконечная — конечная температура tначальная — начальная температура

Также ее можно рассчитать через теплоемкость вещества:

Удельная теплоемкость вещества c= C/m c — удельная теплоемкость вещества [Дж/кг*˚C] C — теплоемкость вещества [Дж/˚C] m — масса

Величины теплоемкость и удельная теплоемкость означают практически одно и то же. Отличие в том, что теплоемкость — это способность всего вещества к передаче тепла. То есть формулу количества теплоты для нагревания тела можно записать в таком виде:

Количество теплоты, необходимое для нагревания тела Q = C(tконечная — tначальная) Q — количество теплоты c — удельная теплоемкость вещества [Дж/кг*˚C] m — масса tконечная — конечная температура tначальная — начальная температура

Онлайн-курсы физики в Skysmart не менее увлекательны, чем наши статьи!

Таблица удельных теплоемкостей

Удельная теплоемкость — табличная величина. Часто ее указывают в условии задачи, но при отсутствии в условии — можно и нужно воспользоваться таблицей. Ниже приведена таблица удельных теплоемкостей для некоторых (многих) веществ.

Газы	C, Дж/(кг·К)
Азот N2	1051
Аммиак NH3	2244
Аргон Ar	523
Ацетилен C2H2	1683
Водород H2	14270
Воздух	1005
Гелий He	5296
Кислород O2	913
Криптон Kr	251
Ксенон Xe	159
Метан CH4	2483
Неон Ne	1038
Оксид азота N2O	913
Оксид азота NO	976
Оксид серы SO2	625
Оксид углерода CO	1043
Пропан C3H8	1863
Сероводород H2S	1026
Углекислый газ CO2	837
Хлор Cl	520
Этан C2H6	1729
Этилен C2H4	1528

Металлы и сплавы	C, Дж/(кг·К)
Алюминий Al	897
Бронза алюминиевая	420
Бронза оловянистая	380
Вольфрам W	134
Дюралюминий	880
Железо Fe	452
Золото Au	129
Константан	410
Латунь	378
Манганин	420
Медь Cu	383
Никель Ni	443
Нихром	460
Олово Sn	228
Платина Pt	133
Ртуть Hg	139
Свинец Pb	128
Серебро Ag	235
Сталь стержневая арматурная	482
Сталь углеродистая	468
Сталь хромистая	460
Титан Ti	520
Уран U	116
Цинк Zn	385
Чугун белый	540
Чугун серый	470

Жидкости	Cp, Дж/(кг·К)
Азотная кислота (100%-ная) NH3	1720
Бензин	2090
Вода	4182
Вода морская	3936
Водный раствор хлорида натрия (25%-ный)	3300
Глицерин	2430
Керосин	2085…2220
Масло подсолнечное рафинированное	1775
Молоко	3906
Нефть	2100
Парафин жидкий (при 50С)	3000
Серная кислота (100%-ная) H2SO4	1380
Скипидар	1800
Спирт метиловый (метанол)	2470
Спирт этиловый (этанол)	2470
Топливо дизельное (солярка)	2010

Задача

Какое твердое вещество массой 2 кг можно нагреть на 10 ˚C, сообщив ему количество теплоты, равное 7560 Дж?

Решение:

Используем формулу для нахождения удельной теплоемкости вещества:

c= Q/m(t_{конечная} — t_{начальная})

Подставим значения из условия задачи:

c= 7560/2*10 = 7560/20 = 378 Дж/кг*˚C

Смотрим в таблицу удельных теплоемкостей для металлов и находим нужное значение.

Металлы и сплавы	C, Дж/(кг·К)
Алюминий Al	897
Бронза алюминиевая	420
Бронза оловянистая	380
Вольфрам W	134
Дюралюминий	880
Железо Fe	452
Золото Au	129
Константан	410
Латунь	378
Манганин	420
Медь Cu	383
Никель Ni	443
Нихром	460
Олово Sn	228
Платина Pt	133
Ртуть Hg	139
Свинец Pb	128
Серебро Ag	235
Сталь стержневая арматурная	482
Сталь углеродистая	468
Сталь хромистая	460
Титан Ti	520
Уран U	116
Цинк Zn	385
Чугун белый	540
Чугун серый	470

Ответ: латунь

Эффект изохорного процесса и его применение

Свойства изохорного процесса, так же как и свойства изобарного и изотермического процессов, широко применяются в современных изобретениях.

Главный эффект изохорного процесса заключается в том, что при неизменном объеме теплоемкость значительно ниже, чем при постоянном давлении. Теплоемкость – величина, показывающая, какое количество теплоты необходимо для нагрева тела на один градус.

В изохорном процессе при изменении температуры система не совершает никакой работы, и, следовательно, вся подведенная теплота расходуется на изменение тепловой энергии: \.

Согласно закону Шарля, в идеальном газе при изохорном процессе изменение давления прямо пропорционально изменению температуры. Однако для неидеальных газов закон Шарля не применим. Так как в этом случае некоторая часть теплоты, сообщаемой газу, расходуется на увеличение энергетического потенциала взаимодействия элементарных частиц.

В бензиновом двигателе внутреннего сгорания, в работе которого в максимальном приближении внедрен идеальный цикл Отто, такты 2-3 и 4-1 являются изохорными процессами. 2-3 – изохорный подвод тепла, 4-1 – изохорный отвод тепла. Работа, которая совершается на выходе мотора, равна разности основных работ. То есть разности между работой, совершаемой газом во время рабочего хода (над поршнем во время третьего такта), и работой, затрачиваемой поршнем на сжатие газа во втором такте. Принудительное сжигание смеси, используемое в таких двигателях, позволяет увеличить степень сжатия газа в 7-12 раз.

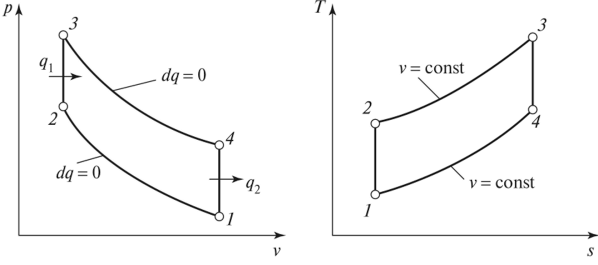Рисунок 2. Цикл Отто

Изохорные такты также присутствуют в двигателях с циклом Стирлинга. В таких двигателях установлен регенератор, обеспечивающий выполнение изохорного процесса в двух тактах. Проходя через наполнитель в одну сторону, газ передает регенератору тепловую энергию рабочего тела. Двигаясь в обратном направлении, газ снова возвращает энергию рабочей системе. КПД и обратимость идеального цикла Стирлинга равны показателям цикла Карно.

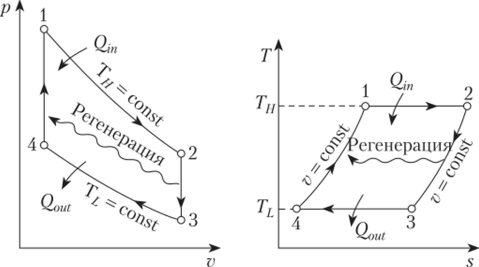Рисунок 3. Цикл Стирлинга

Также изохорный подвод тепла используется в циклах ГТУ – газотурбинных установок.

Популярные статьи

Сила Лоренца
Физика

Преимущества и недостатки рыночной экономики
Экономика

Правила речевого этикета
Русский язык

Уравнение Майера
Физика

Формула производной от дроби, примеры
Математика

Что такое производная сложной функции и как её найти
Математика

Конституционные обязанности человека и гражданина
Право и юриспруденция

Черты личности и структура характера
Психология

Итоги Великой французской революции
История

Понятие и признаки общества
Социология

Изохорная теплоемкость

Изменение энтропии ds.

Вычислим изохорную теплоемкость влажного водяного пара, имеющего степень сухости х 0 575 при давлении 1 бар. Поданным опытов А. М. Керимова, теплоемкости су и су при давлении р 1 бар равны соответственно 1 007 и 16 95 ккал / кг. Непосредственное вычисление по таблицам водяного пара дает значение cv 10 1 ккал / ( кг — град), практически не отличающееся от экспериментального.
 

Так как изохорная теплоемкость влажного пара cv — величина положительная, то это значит, что знаки дифференциалов dp и dv противоположны.
 

Так как изохорная теплоемкость влажного пара cv — величина положительная, то величины dp и dv — противоположны. Таким образом, изоэнтропическое расширение влажного пара обусловливает уменьшение его давления и температуры, а изоэнтропическое сжатие — возрастание их.
 

Так как изохорная теплоемкость влажного пара с есть положительная величина, то отсюда следует, что знаки дифференциалов dp и dv противоположны.
 

Результаты исследований изохорной теплоемкости на изохорах, проведенные вдали от критической точки v 2 67; 2 92; 4 95; 5 96; 9 92 см3 / г, показывают, что теплоемкость cv с увеличением температуры монотонно увеличивается, достигает некоторого своего максимального значения при определенной температуре, затем происходит скачкообразное ее уменьшение, что является признаком совершения перехода из двухфазного состояния в однофазное через пограничную кривую. В однофазной области в исследованном температурном интервале теплоемкость с на изохорах раствора данной концентрации с увеличением температуры монотонно уменьшается. Установлено, что величины теплоемкости сс в двухфазной области и их разрыв при переходе в однофазное состояние с ростом значения v возрастают.
 

Экспериментальное исследование изохорной теплоемкости некоторых углеводородов и спиртов.
 

Характер сингулярности изохорной теплоемкости одноком понентной жидкости таков, что до сих пор можно встретит утверждения, основанные на рассмотрении искаженного участ ка аномалии, об отсутствии расходимости этой величины в кри тической точке.
 

Уравнение для изохорной теплоемкости са записывается следующим образом ( г V сопз.
 

Следовательно, изохорную теплоемкость можно определить как количество теплоты, которое необходимо подвести к системе при постоянном объеме, чтобы повысить ее температуру на один градус.
 

Здесь Су — изохорная теплоемкость в идеальном состоянии, отнесенная к одной частице газа; Л, Л / — число положительных ионов и электронов.
 

Покажите, что изохорная теплоемкость этого газа не зависит от объема.
 

С г — изохорная теплоемкость газа; i CPICV; Pt и Р2 — начальное и конечное давление; СР — изобарная теплоемкость газа; TI и TZ — начальная и конечная температура; Vi и У2 — — начальный и конечный объем.
 

Зависимость изохорной теплоемкости от температуры для простых кристаллических веществ.| Изобарная теплоемкость металлов.

Таким образом, изохорная теплоемкость кристалла простого вещества должна быть равна 25 Дж / ( К-моль), Это правило соблюдается только при достаточно высоких температурах для многих металлов, начиная с четвертого периода системы элементов. Чем больше атомная масса элемента, тем при более низкой температуре достигается теоретическое значение теплоемкости. Теплоемкость алмаза не достигает этого значения даже при 1200 С.
 

Примеры теплоаккумуляторов в жизни

Что это может быть? К примеру, какие-то внутренние кирпичные стены, большая печь или камин, стяжки из бетона.

Мебель в любом доме или квартире является отличным теплоаккумулятором, ведь фанера, ДСП и дерево фактически в три раза больше могут запасаться теплом лишь на килограмм веса, нежели пресловутый кирпич.

Есть ли недостатки в теплоаккумуляторах? Конечно, главный минус данного подхода состоит в том, что теплоаккумулятор требуется проектировать еще на стадии создания макета каркасного дома. Все из-за того, что он отличается большим весом, и это потребуется учесть при создании фундамента, а после еще представить, как данный объект будет интегрирован в интерьер. Стоит сказать, что учитывать придется не только массу, потребуется оценивать в работе обе характеристики: массу и теплоемкость. К примеру, если применять золото с невероятным весом в двадцать тонн на кубометр в качестве теплоаккумулятора, то продукция будет функционировать как нужно лишь на двадцать три процента лучше, нежели бетонный куб, вес которого составляет две с половиной тонны.

От: admin

Эта тема закрыта для публикации ответов.

Расчёт

Выполним расчёт C_P воды и олова при следующих условиях:

• m = 500 грамм;
• t1 =24ºC и t2 = 80ºC – для воды;
• t1 =20ºC и t2 =180ºC – для олова;
• Q = 28 тыс. Дж.

Для начала определяем ΔT для воды и олова соответственно:

• ΔТв = t2–t1 = 80–24 = 56ºC
• ΔТо = t2–t1 = 180–20 =160ºC

Затем находим удельную теплоёмкость:

1. с=Q/(m*ΔТв)= 28 тыс. Дж/(500 г *56ºC) = 28 тыс.Дж/(28 тыс.г*ºC) = 1 Дж/г*ºC.
2. с=Q/(m*ΔТо)=28тыс.Дж/(500 гр*160ºC)=28 тыс.Дж/(80 тыс.г*ºC)=0,35 Дж/г*ºC.

Таким образом, удельная теплоемкость воды составила 1 Дж/г *ºC, а олова 0,35 Дж/г*ºC. Отсюда можно сделать вывод о том, что при равном значении подводимого тепла в 28 тыс. Дж олово нагрется быстрее воды, поскольку его теплоёмкость меньше.

Теплоёмкостью обладают не только газы, жидкости и твёрдые тела, но и продукты питания.

Вырожденный газ

Для вырожденного электронного газа в металлах теплоёмкость определяется формулой

cVe=23m∗32ℏ3μ12kB2T{\displaystyle c_{V}^{e}={\frac {\sqrt {2}}{3}}{\frac {m^{*3/2}}{\hbar ^{3}}}\mu _{0}^{1/2}k_{B}^{2}T},

где m∗{\displaystyle m^{*}} — эффективная масса электронов, ℏ{\displaystyle \hbar } — приведённая постоянная Планка, kB{\displaystyle k_{B}} — постоянная Больцмана, μ{\displaystyle \mu _{0}} — энергия уровня Ферми, T — температура.

Теплоёмкость стремится к нулю при малых температурах, удовлетворяя теореме Нернста и линейно возрастает с температурой. Поскольку теплоёмкость кристаллической решётки при низких температурах пропорциональная кубу температуры (см. закон Дебая), то существует область низких температур, при которых теплоёмкость электронов больше чем теплоёмкость решётки. Однако при более высоких температурах, чем температура Дебая, вклад электронной подсистемы в общую теплоёмкость твёрдого тела не превышает нескольких процентов. Для этих температур справедливо

cVecVL≈kbTμ{\displaystyle {\frac {c_{V}^{e}}{c_{V}^{L}}}\approx {\frac {k_{b}T}{\mu _{0}}}},

где cVL{\displaystyle c_{V}^{L}} — теплоёмкость кристаллической решётки.

Объясняется такое соотношение тем, что вклад в электронную теплоёмкость вносят лишь те электроны, которые имеют энергию, близкую к энергии Ферми. Электроны с энергиями, намного меньшими, чем энергия уровня Ферми, не могут получать тепло, поскольку для увеличения энергии им нужно было бы перейти на близкие энергетические уровни внутри зоны, уже занятые другими электронами. Из-за принципа Паули переход в занятое другим электроном состояние невозможен.

Практические примеры

Первый пример

Учитывая (идеальный) газ, заключенный в цилиндр с поршнем, укажите, являются ли следующие случаи примерами изохорных процессов..

— 500 Дж работа на газе.

В этом случае это не будет изохорный процесс, поскольку для выполнения работы с газом необходимо его сжать, а значит, изменить его объем..

— Газ расширяется за счет горизонтального смещения поршня.

Опять же, это не был бы изохорный процесс, учитывая, что расширение газа подразумевает изменение его объема..

— Поршень цилиндра закреплен так, что его нельзя сместить, а газ охлаждают.

В этом случае это будет изохорный процесс, поскольку не будет изменений объема.

Второй пример

Определите изменение внутренней энергии, которое будет испытывать газ, содержащийся в контейнере объемом 10 л, который подвергается воздействию 1 атм давления, если его температура поднимается от 34ºC до 60ºC в изохорном процессе, известном его удельной молярной теплотой С_v = 2,5 ·R (будучи R = 8,31 Дж / моль · К).

Поскольку это процесс с постоянным объемом, изменение внутренней энергии будет происходить только вследствие тепла, подаваемого в газ. Это определяется по следующей формуле:

Q_v = n ∙ C_v  T ΔT

Чтобы рассчитать подводимое тепло, сначала необходимо рассчитать количество молей газа, содержащегося в контейнере. Для этого необходимо прибегнуть к уравнению идеальных газов:

P ∙ V = n ∙ R ∙ T

В этом уравнении n — число молей, R — постоянная, значение которой составляет 8,31 Дж / моль · K, T — температура, P — давление, которому подвергается газ, измеренный в атмосферах, и T — температура. измеряется в кельвинах.

Очисти и получишь:

n = R ∙ T / (P ∙ V) = 0, 39 молей

Так что:

Δ U = Q_В  = n ∙ C_v  T ΔT = 0,39 ∙ 2,5 ∙ 8,31 ∙ 26 = 210,65 Дж

Первый закон термодинамики для изохорного процесса

Формула

Формула первого закона термодинамики имеет следующий вид:

\

Где Q – количество теплоты, \ – сумма изменения внутренней энергии, A – работа системы.

Закон подразумевает, что для каких-либо изменений внутри системы необходимо приложить внешние усилия. Таким образом, можно предложить следующую простейшую формулировку первого закона термодинамики: для изменения внутренней энергии некоторой системы требуется внешнее воздействие. Именно этот закон доказывает невозможность изобретения вечного двигателя, над которым так долго бились ведущие ученые разных стран.

Изохорный процесс:

• Процесс, происходящий с газом неизменной массы при постоянном объеме называется изохорным.
• Закон Шарля: при изохорном нагревании газа относительное изменение его давления пропорционально конечной температуре.

\

Как уже отмечалось, изохорным процессом в термодинамике считается физическое явление, протекающее при постоянном объеме. То есть при изменении температуры некоторого газа, находящегося внутри сосуда, его объем не изменится. Следовательно, работа, совершаемая газом при \, равна нулю, т.е. A=0.

Формула

Таким образом, первый закон термодинамики для изохорного процесса выражается следующей формулой:

\

Где \ – внутренняя энергия идеального газа при начальной температуре, \ – внутренняя энергия идеального газа при конечной температуре.

При изохорном нагреве внутренняя энергия газа возрастает за счет поглощения тепла \, а при охлаждении газ отдает тепло и его внутренняя энергия уменьшается \.

Изучения термодинамических изменений подразумевает под собой определение следующих параметров: работы, которая была совершена в данном процессе, изменения внутренней энергии и количества теплоты. Также определяется взаимосвязь некоторых величие, характеризующих состояние газа.  

Исследование изохорических процессов проводится по следующему методу:

• устанавливается взаимосвязь показателями рабочего тела на начальный и конечный момент, то есть выводится физическое уравнение;
• определяется работа, совершаемая газом, при изменении объема;
• определяется количество подводимой/отводимой  теплоты;
• вычисляется изменение внутренней энергии и энтропии (функции состояния исследуемой системы).

Нет времени решать самому?

Наши эксперты помогут!

Контрольная

| от 300 ₽ |

Реферат

| от 500 ₽ |

Курсовая

| от 1 000 ₽ |

Нужна помощь

Теплоотдача и терморегуляция

Количество
теплоты Q,
переносимое вследствие теплопро­водности
за время Δt,
определяется формулой

Q=k₁ΔTΔSΔt/Δx

где
k₁—
коэффициент теплопроводности; ΔT/Δx
— градиент тем-

пературы
в направлении, перпендикулярном площадке
ΔS.

Количество
теплоты Q,
переносимое вследствие конвекции за
время Δt,
определяется формулой;

Q=k₂(T-T)ΔSΔt

где
k₂
— коэффициент теплопередачи при
конвекции; Т и Т
— соответственно
температуры поверхности ΔS
и омываемой среды.

Количество
теплоты Q,
излучаемое за время Δt
абсолютно черным телом, определяется
формулой (закон Стефана — Больцмана)

Q=σT4ΔSΔt

где
σ—
постоянная Стефана — Больцмана; Т
— абсолютная температура
тела; ΔS
— площадь излучающей поверхности тела.
Для
реальных физических тел закон Стефана
— Больцмана имеет
вид

Q=k₃σT4ΔSΔt

где
k₃
— коэффициент, учитывающий, что свойства
поверхности реальных
физических тел отличны от свойств
поверхности абсолютно
черного тела (k₃<. k>3=
1.

При
наличии двух встречных потоков радиации
от излу­чающей
поверхности к среде и от среды к
поверхности закон Стефана
— Больцмана имеет вид

Q=k₃σ(T4–T4)ΔSΔt

где
Т и Т
— абсолютные температуры тела и
среды; ΔS
— площадь
излучающей поверхности тела.

Длина
волны λ_т,
которой соответствует максимум
излуча-тельной способности черного
тела, обратно пропорциональна абсолютной
температуре Т (закон смещения Вина):

λ_m=b/T

где
b
— постоянная закона смещения Вина.

Удельная, молярная и объёмная теплоёмкости

Основные статьи: Удельная теплоёмкость, Молярная теплоёмкость и Объёмная теплоёмкость

Очевидно, что чем больше масса тела, тем больше требуется теплоты для его нагревания, и теплоёмкость тела пропорциональна количеству вещества, содержащегося в нём. Количество вещества может характеризоваться массой или количеством молей. Поэтому удобно пользоваться понятиями удельной теплоёмкости (теплоёмкости единицы массы тела):

c=Cm{\displaystyle c={C \over m}}

и молярной теплоёмкости (теплоёмкости одного моля вещества):

Cμ=Cν,{\displaystyle C_{\mu }={C \over \nu },}

где ν=mμ{\displaystyle \nu ={m \over \mu }} — количество вещества в теле; m{\displaystyle m} — масса тела; μ{\displaystyle \mu } — молярная масса. Молярная и удельная теплоёмкости связаны соотношением Cμ=cμ{\displaystyle C_{\mu }=c\mu }.

Объёмная теплоёмкость (теплоёмкость единицы объёма тела):

C′=CV.{\displaystyle C’={C \over V}.}

В) Влияние параметров состояния газа на его теплоемкость

Теплоемкость
идеального газа зависит только от
температуры и увеличивается при
увеличении Т
.

Одноатомные газы
представляют исключение, т.к. их
теплоемкость практически не зависит
от температуры.

Классическая
молекулярно-кинетическая теория газов
позволяет довольно точно определить
теплоемкости одноатомных идеальных
газов в широком диапазоне температур
и теплоемкости многих двухатомных (и
даже трехатомных) газов при невысоких
температурах.

Но при температурах,
существенно отличных от 0 о С,
экспериментальные значения теплоемкости
двух- и многоатомных газов оказываются
значительно отличающимися от предсказанных
молекулярно-кинетической теорией.

с
v
Т

В теплотехнических
расчетах обычно пользуются опытными
значениями теплоемкости газов,
представленными в виде таблиц. При этом
теплоемкость, определенная в опыте (при
данной температуре), называется истинной


теплоемкостью. А если в опыте измерялось
количество теплоты q
,
которое было затрачено на существенное
повышение температуры 1 кг газа от
некоторой температуры T
0
до
температуры
T
,
т.е. на Т

= Т

T
0
, то отношение

называется средней


теплоемкостью газа в данном интервале
температур.

Обычно в справочных
таблицах значения средней теплоемкости
даются при значении T
0
, соответствующем
нулю градусов Цельсия.

Теплоемкость
реального
газа


зависит, кроме температуры, также и от
давления из-за влияния сил межмолекулярного
взаимодействия.

Учитывая, что теплоемкость непостоянна,
а зависит от температуры и других
термических параметров, различают
истинную и среднюю теплоемкости. Истинная
теплоемкость выражается уравнением
(2.2) при определенных параметрах
термодинамического процесса, то есть
в данном состоянии рабочего тела. В
частности, если хотят подчеркнуть
зависимость теплоёмкости рабочего тела
от температуры, то записывают её как
,
а удельную – как.
Обычно под истинной теплоёмкостью
понимают отношение элементарного
количества теплоты, которое сообщается
термодинамической системе в каком-либо
процессе к бесконечно малому приращению
температуры этой системы, вызванному
сообщенной теплотой. Будем считатьистинной
теплоёмкостью термодинамической системы
при температуре системы равной,
а-
истинной удельной теплоёмкостью рабочего
тела при его температуре равной.
Тогда среднюю удельную теплоёмкость
рабочего тела при изменении его
температуры отдоможно
определить как

Обычно в таблицах приводятся средние
значения теплоемкости
для
различных интервалов температур,
начинающихся с.
Поэтому во всех случаях, когда
термодинамический процесс проходит в
интервале температур отдо,
в котором,
количество удельной теплотыпроцесса
определяется с использованием табличных
значений средних теплоемкостейследующим
образом:

.

Значения средних теплоемкостей
и,
находят по таблицам.

Краткая теория и методика выполнения работы

Удельной
теплоемкостью
вещества называется величина, равная
количеству теплоты, которую необходимо
сообщить единице массы вещества для
увеличения ее температуры на один градус
Кельвина:

. (4.1)

Теплоемкость
одного моля вещества называется молярной
теплоемкостью:

, (4.2)

где
m – масса, µ – молярная масса вещества,– число молей газа.

Значение
теплоемкости газов зависит от условий
их нагревания. В соответствии с первым
законом термодинамики количество
теплоты,
сообщенное системе, расходуется на
увеличение ее внутренней энергиии на совершение системой работыпротив внешних сил:

. (4.3)

Изменение
внутренней энергии идеального газа в
случае изменения его температурыравно:

, (4.4)

здесь
– число степеней свободы молекулы газа,
под которым подразумевается число
независимых координат, полностью
определяющих положение молекулы в
пространстве;– универсальная газовая постоянная.

При
расширении газа система совершает
работу:

. (4.5)

Если
газ нагревать при постоянном объеме
(),
тои, согласно (4.3), все полученное газом
количество теплоты расходуется только
на увеличение его внутренней энергии.
Следовательно, учитывая (4.4), молярная
теплоемкость идеального газа при
постоянном объеме будет равна:

. (4.6)

Если
газ нагревать при постоянном давление
(),
то полученное газом количество теплоты
расходуется на увеличение его внутренней
энергиии совершение газом работы:

.

Тогда
молярная теплоемкость идеального газа
при постоянном давлении определяется
следующим образом:

. (4.7)

Используя
уравнение состояния идеального газа
(уравнение Клапейрона–Менделеева),
можно показать, что для одного моля газа
справедливо соотношение:

,

поэтому:

.

Последнее выражение
называют уравнением Майера. Из него,
учитывая (4.6), получаем:

. (4.8)

Отношение
теплоемкостейобозначаюти называют показателем адиабаты или
коэффициентом Пуассона:

. (4.9)

Адиабатным
называется процесс, протекающий в
термоизолированной системе, т.е. без
теплообмена с окружающей средой,.

На
практике он может быть осуществлен в
системе, окруженной теплоизоляционной
оболочкой, но поскольку для теплообмена
необходимо некоторое время, то адиабатным
можно считать также процесс, который
протекает так быстро, что система не
успевает вступить в теплообмен с
окружающей средой.

Первый
закон термодинамики для адиабатного
процесса имеет вид.
Знак минус говорит о том, что при
адиабатном процессе система может
совершать работу только за счет внутренней
энергии. С учетом (4.4)–(4.6) имеем:

. (4.10)

Продифференцировав
уравнение Клапейрона–Менделеева,
получим:

.

Выразим
из негои подставим в формулу (4.10):

.

Выразивиз уравнения Майера и учитывая соотношение
(4.8), получим:

.

Интегрируя
данное дифференциальное уравнение при
условииполучим выражение:

.
(4.11)

Уравнение
(4.11) называется уравнением адиабаты или
уравнением Пуассона.

Метод
определения показателя адиабаты,
предложенный Клеманом и Дезормом (1819
г.), основывается на изучении параметров
некоторой массы газа, переходящей из
одного состояния в другое двумя
последовательными процессами –
адиабатным и изохорным. Эти процессы
на диаграмме–(рис. 4.1) изображены кривыми соответственно
1–2 и 2–3.

Если
в сосуд, соединенный с дифференциальным
датчиком давления, накачать воздух и
подождать до установления теплового
равновесия с окружающей средой, то в
этом начальном состоянии 1 газ имеет
параметры,,,
причем температура газа в сосуде равна
температуре окружающей среды,
а давлениенемного больше атмосферного.

Если
теперь на короткое время соединить
сосуд с атмосферой, то произойдет
адиабатное расширение воздуха. При этом
воздух в сосуде перейдет в состояние
2, его давление понизится до атмосферного.
Масса воздуха, оставшегося в сосуде,
которая в состоянии 1 занимала часть
объема сосуда, расширяясь, займет весь
объем.
При этом температура воздуха, оставшегося
в сосуде, понизится до.
Поскольку процесс 1–2 – адиабатный, к
нему можно применить уравнение Пуассона
(4.11):

или.

Отсюда:

. (4.12)

После
кратковременного соединения сосуда с
атмосферой охлажденный из-за адиабатного
расширения воздух в сосуде будет
нагреваться (процесс 2–3) до температуры
окружающей средыпри постоянном объеме.
При этом давление в сосуде поднимется
до.

Поскольку
процесс 2–3 – изохорный, к нему можно
применить закон Шарля:

или

. (4.13)

Из уравнений (4.12)
и (4.13) получим:

.

Прологарифмируем
это выражение:

.

Поскольку
избыточные давленияиочень малы по сравнению с атмосферным
давлением,
а также учитывая, что при,
будем иметь:

.

Откуда:

. (4.14)

Избыточные
давленияиизмеряют с помощью дифференциального
датчика давления.

Таблица удельной теплоемкости пищевых продуктов

В таблице приведены значения средней удельной теплоемкости пищевых продуктов (овощей, фруктов, мяса, рыбы, хлеба, вина и т. д.) в диапазоне температуры 5…20°С и нормальном атмосферном давлении.

Таблица удельной теплоемкости продуктов питания

Продукты	C, Дж/(кг·К)
Абрикосы	3770
Ананасы	3684
Апельсины	3730
Арбуз	3940
Баклажаны	3935
Брюква	3810
Ветчина	2140
Вино крепленое	3690
Вино сухое	3750
Виноград	3550
Вишня	3650
Говядина и баранина жирная	2930
Говядина и баранина маложирная	3520
Горох	3684
Грибы свежие	3894
Груши	3680
Дрожжи прессованные	1550…3516
Дыни	3850
Ежевика	3642
Земляника	3684
Зерно пшеничное	1465…1549
Кабачки	3900
Капуста	3940
Картофель	3430
Клубника	3810
Колбасы	1930…2810
Крыжовник	3890
Лимоны	3726
Лук	2638
Макароны не приготовленные	1662
Малина	3480
Мандарины	3770
Маргарин сливочный	2140…3182
Масло анисовое	1846
Масло мятное	2080
Масло сливочное	2890…3100
Масло сливочное топленое	2180
Мед	2300…2428
Молоко сухое	1715…2090
Морковь	3140
Мороженое (при -10С)	2175
Мука	1720
Огурцы	4060
Пастила	2090
Патока	2512…2700
Перец сладкий	3935
Печенье	2170
Помидоры	3980
Пряники	1800…1930
Редис	3970
Рыба жирная	2930
Рыба нежирная	3520
Салат зеленый	4061
Сало топленое	2510
Сахар кусковой	1340
Сахарный песок	720
Свекла	3340
Свинина жирная	260
Свинина нежирная	3010
Слива	3750
Сметана	3010
Смородина черная	3740
Сода	2256
Соль поваренная (2% влажности)	920
Спаржа	3935
Сыр жирный	2430
Творог	3180
Телятина жирная	3180
Телятина нежирная	3520
Тесто заварное	2910
Тыква	3977
Хлеб (корка)	1680
Хлеб (мякиш)	2800
Черешня	3770
Чернослив	3181
Чеснок	3140
Шоколад	2340…2970
Шпинат	3977
Яблоки	3760
Яйцо куриное	3180

Кроме таблиц удельной теплоемкости, вы также можете ознакомиться с подробнейшей таблицей плотности веществ и материалов, которая содержит данные по величине плотности более 500 веществ (металлов, пластика, резины, продуктов, стекла и др.).

1. Исаченко В. П., Осипова В. А., Сукомел А. С. Теплопередача. Учебник для вузов, изд. 3-е, перераб. и доп. — М.: «Энергия», 1975.
2. Тепловые свойства металлов и сплавов. Справочник. Лариков Л. Н., Юрченко Ю. Ф. — Киев: Наукова думка, 1985. — 439 с.
3. Физические величины. Справочник. А. П. Бабичев, Н. А. Бабушкина, А. М. Братковский и др. Под ред. И. С. Григорьева — М.: Энергоатомиздат, 1991. — 1232 с.
4. Еремкин А. И., Королева Т. И. Тепловой режим зданий: Учебное пособие. — М.: Издательство ACB, 2000 — 368 с.
5. Кириллов П. Л., Богословская Г. П. Тепломассобмен в ядерных энергетических установках: Учебник для вузов.
6. Михеев М. А., Михеева И. М. Основы теплопередачи. Изд. 2-е, стереотип. М.: «Энергия», 1977. — 344 с. с ил.
7. Казанцев Е. И. Промышленные печи. Справочное руководство для расчетов и проектирования.
8. Франчук А. У. Таблицы теплотехнических показателей строительных материалов, М.: НИИ строительной физики, 1969 — 142 с.
9. Добрынин В. М., Вендельштейн Б. Ю., Кожевников Д. А. Петрофизика: Учеб. для вузов. 2-ое изд. перераб. и доп. под редакцией доктора физико-математических наук Д. А. Кожевникова — М.: ФГУП Издательство «Нефть и газ» РГУ нефти и газа им. И.М. Губкина, 2004. — 368 с., ил.
10. В. Блази. Справочник проектировщика. Строительная физика. М.: Техносфера, 2005. — 536 с.
11. Енохович А. С. Справочник по физике. М.: «Просвещение», 1978. — 415 с. с ил.
12. Строительная теплотехника СНиП II-3-79. Минстрой России — Москва 1995.
13. Мустафаев Р. А. Теплофизические свойства углеводородов при высоких параметрах состояния. М.: Энергоатомиздат, 1991. — 312 с.
14. Новиченок Н. Л., Шульман З. П. Теплофизические свойства полимеров. Минск, «Наука и техника» 1971. — 120 с.
15. Шелудяк Ю. Е., Кашпоров Л. Я. и др. Теплофизические свойства компонентов горючих систем. М., 1992. — 184 с.