Объемный расход — volumetric flow rate

Подходящая скорость жидкости, в зависимости от вида трубопровода

Прежде всего учитываются минимальные затраты, без которых невозможно перекачивать жидкость. Кроме того, обязательно рассматривается стоимость трубопровода.

При расчете, нужно всегда помнить об ограничениях скорости двигающейся среды. В некоторых случаях, размер магистрального трубопровода должен отвечать требованиям, заложенным в технологический процесс.

На габариты трубопровода влияют также возможные скачки давления.

Когда делаются предварительные расчеты, изменение давление в расчет не берется. За основу проектирования технологического трубопровода берется допустимая скорость.

Когда в проектируемом трубопроводе существуют изменения направления движения, поверхность трубы начинает испытывать большое давление, направленное перпендикулярно движению потока.

Такое увеличение связано с несколькими показателями:

• Скорость жидкости;
• Плотность;
• Исходное давление (напор).

Причем скорость всегда находится в обратной пропорции к диаметру трубы. Именно поэтому для высокоскоростных жидкостей требуется правильный выбор конфигурации, грамотный подбор габаритов трубопровода.

Уравнение неразрывности

Характерной чертой несжимаемых жидкостей является то, что масса жидкости сохраняется с помощью двух секций. По этой причине выполняется уравнение неразрывности, которое устанавливает следующую связь:

ρ₁ К₁ V₁ = ρ₂ К₂ V₂

В этом уравнении ρ — плотность жидкости.

Для случаев режимов постоянного потока, в которых плотность постоянна и, следовательно, верно, что ρ₁ = ρ₂, сводится к следующему выражению:

К₁ V₁ = А₂ V₂

Это равносильно утверждению, что поток сохраняется и, следовательно:

Q₁ = Q₂.

Из наблюдений выше следует, что жидкости ускоряются, когда достигают более узкого участка трубопровода, и замедляются, когда достигают более широкого участка канала. Этот факт имеет интересные практические приложения, поскольку позволяет играть со скоростью движения жидкости.

Стационарное течение жидкости. Уравнение неразрывности

Рассмотрим случай, когда невязкая жидкость течет по горизонтальной цилиндрической трубе с изменяющимся поперечным сечением.

Течение жидкости называют стационарным, если в каждой точке пространства, занимаемого жидкостью, ее скорость с течением времени не изменяется. При стационарном течении через любое поперечное сечение трубы за равные промежутки времени переносятся одинаковые объемы жидкости.

Жидкости практически несжимаемы, т. е. можно считать, что данная масса жидкости всегда имеет неизменный объем. Поэтому одинаковость объемов жидкости, проходящих через разные сечения трубы, означает, что скорость течения жидкости зависит от сечения трубы.

Пусть скорости стационарного течения жидкости через сечения трубы S₁ и S₂ равны соответственно v₁ и v₂. Объем жидкости, протекающей за промежуток времени t через сечение S₁, равен V₁=S₁v₁t, а объем жидкости, протекающей за то же время через сечение S2, равен V₂=S₂v₂t. Из равенства V₁=V₂ следует, что

S₁V₁=S₂V₂. (5.10)

Соотношение (5.10) называют уравнением неразрывности. Из него следует, что

v₁/v₂=S₂/S₁.

Следовательно, при стационарном течении жидкости скорости движения ее частиц через разные поперечные сечения трубы обратно пропорциональны площадям этих сечений.

Согласно второму закону Ньютона, причиной ускорения является сила. Этой силой в данном случае является разность сил давления, действующих на текущую жидкость в широкой и узкой частях трубы. Следовательно, б широкой части трубы давление жидкости должно быть больше, чем в узкой. Это можно непосредственно наблюдать на опыте. На рис. показано, что на участках разного поперечного сечения S₁ и S₂ в трубу, по которой течет жидкость, вставлены манометрические трубки.

Как показывают наблюдения, уровень жидкости в манометрической трубке у сечения S₁ трубы выше, чем у сечения S₂. Следовательно, давление в жидкости, протекающей через сечение с большей площадью S₁, выше, чем давление в жидкости, протекающей через сечение с меньшей площадью S₂. Следовательно, при стационарном течении жидкости в тех местах, где скорость течения меньше, давление в жидкости больше и, наоборот, там, где скорость течения больше, давление в жидкости меньше. К этому выводу впервые пришел Бернулли, поэтому данный закон называется законом Бернулли.

Закон Бернулли является следствием закона сохранения энергии для стационарного потока идеальной (то есть без внутреннего трения) несжимаемой жидкости:

Здесь

ρ — плотность жидкости,

v — скорость потока,

h — высота, на которой находится рассматриваемый элемент жидкости,

p — давление.

Константа в правой части обычно называется напором, или полным давлением. Размерность всех слагаемых — единица энергии, приходящейся на единицу объёма жидкости.

Это соотношение называют уравнением Бернулли. Величина в левой части имеет отношение к интегралу Бернулли.

Для горизонтальной трубы h = const и уравнение Бернулли принимает вид .

Согласно закону Бернулли полное давление в установившемся потоке жидкости остается постоянным вдоль этого потока. Полное давление состоит из весового, статического и динамического давления. Из закона Бернулли следует, что при уменьшении сечения потока, из-за возрастания скорости, то есть динамического давления, статическое давление падает. Закон Бернулли справедлив и для ламинарных потоков газа. Явление понижения давления при увеличении скорости потока лежит в основе работы различного рода расходомеров, водо- и пароструйных насосов.

Закон Бернулли справедлив в чистом виде только для жидкостей, вязкость которых равна нулю, то есть таких жидкостей, которые не прилипают к поверхности трубы. На самом деле экспериментально установлено, что скорость жидкости на поверхности твердого тела всегда в точности равна нулю.

Закон Бернулли можно применить к истечению идеальной несжимаемой жидкости через малое отверстие в боковой стенке или дне широкого сосуда.

Согласно закону Бернулли приравняем полные давления на верхней поверхности жидкости и на выходе из отверстия:

,

где

p — атмосферное давление,

h — высота столба жидкости в сосуде,

v — скорость истечения жидкости.

Отсюда: . Это — формула Торричелли. Она показывает, что при истечении идеальной несжимаемой жидкости из отверстия в широком сосуде жидкость приобретает скорость, какую получило бы тело, свободно падающее с высоты h.

Относительный расход — жидкость

Относительный расход жидкости /, умноженный на максимальный расход ее через клапан, равен действительному расходу жидкости через клапан. Следовательно, коэффициент передачи клапана является функцией действительного расхода жидкости и не зависит от размеров клапана. Это одна из причин, обусловивших широкое использование клапанов с логарифмической характеристикой.
 

Общий вид зависимостей qf ( x.

По оси ординат здесь отложен относительный расход жидкости в ядре потока x3 G K / GCM. МВт / м2, при паросодержаниях, близких к граничным, кривые Xa f ( x) выходят на горизонтальные линии.
 

На рис. 2.23 показано изменение относительного расхода жидкости в пленке xz, равное отношению расхода жидкости в пленке т2 к общему расходу смеси в канале. На графике по оси абсцисс дается массовое расходное паросодержание жп. В проведен комплекс экспериментальных работ по дисперсно-кольцевому режиму течения в диапазоне давлений от 4 0 до 7 0 МПа и удельных массовых расходов 500 — 4000 кг / м2 — с и расходных паросодержапий х от 0 1 до 0 9 в трубах диаметром 13 3 мм.
 

На рис. 5 сравниваются значения относительного расхода жидкости в пленке хг, полученные численно, с прямыми экспериментальными данными , где измерялись расходы жидкости в пленке в зависимости от и, хг и qw при р 69 бар, D 12 6 мм на расстоянии 290J9 от входа в трубу. Анализ опытных данных показывает, что они получены приблизительно с 20 % — ной точностью.
 

П-14 изображены кривые изменения температуры и относительного расхода жидкости, выходящей из теплообменника. Регулирование температуры жидкости на выходе из теплообменника осуществляется путем изменения подачи водяного пара. При возрастании расхода жидкости до 80 % температура ее на выходе изменяется без колебаний. При уменьшении расхода жидкости до 40 % демпфирование колебаний контура регулирования уменьшается, но все же остается достаточно большим, и лишь при уменьшении расхода до 20 % контур регулирования обеспечивает сглаживание колебаний до ] / 4 амплитуды за один период. Описанное явление аналогично изменению диапазона пропорциональности регулятора. При этом чем слабее демпфирование, тем дальше регулируемый параметр устанавливается от заданного значения. Такое влияние противоположно влиянию изменения диапазона пропорциональности регулятора ( см. рис. 1 — 7), Различие кривых переходного процесса вызвано изменением коэффициента передачи объекта, который слабее демпфирован, и более чувствителен к возмущениям при малых объемных скоростях жидкости.
 

Зависимость / от т для трубопровода с клапаном, имеющим логарифмическую характеристику, при различных отношениях С0 / Св.

На рис. П-6 дан график зависимости относительного расхода жидкости от положения штока клапана, который при постоянном Ар совпадает с графиком зависимости относительного открытия клапана от относительного положения штока. В частности, у клапана с линейной характеристикой относительное открытие прямо пропорционально относительному положению штока.
 

Осредненные зависимости тем — Осредненные зависимости пов добычи нефти Гн и обводненности нефтеотдачи г от относительного от-добываемой продукции Ьв от нефтеотдачи пластов т при различной вязкости.

Эта зависимость показывает, при каком относительном расходе жидкости ( воды) получена конкретная нефтеотдача пластов. Удельный расход жидкости или объем нагнетаемой воды на единицу добываемой нефти служит показателем эффективности заводнения залежей.
 

При выводе этой формулы считалось, что невелико влияние вязкостей и относительного расхода жидкости.
 

Соотношение между скоростью газового потока V, расходом жидкости L и перепадом давления ДР в насадочной колонне.| I Характеристика наиболее распространенных насадок.

Диаметр абсорбционной колонны определяется двумя факторами, первым из них является достижение удовлетворительного относительного расхода жидкости и газа, а вторым — наиболее экономичными размерами башни. При низких расходах жидкости и газа образуются регулярные струйки жидкости, стекающей с насадки. Пока все ваши знакомые сидят на месте и не знают чем себя занять, можете на ваших компьютерах включить один крайне необычного формата жесткий секс с болью https://порно.me/bolno , который позволит вам получать безмерное наслаждение от увиденного и желать повторить судьбу наших героях. По крайней мере мужика, который только и кайфует от ситуации.
 

В табл. 6.5 приведены результаты вычислений значений относительного рабочего расхода Qp / QHac в зависимости от относительного давления ( ре-рн) / Рнас и относительного расхода жидкости во вспомогательном контуре х Фн / Фнас-Порядок вычислений следующий.
 

Зависимость медианного диаметра.

Расход

Рассмотрим следующий фактор – расход воды. Он напрямую зависит от давления, и чем оно больше, тем быстрее вода будет двигаться по трубам. То есть будет больший расход. Но все дело в том, что на скорость воды влияет сечение трубы, по которой она двигается. И если уменьшать сечение трубы, то будет расти сопротивление воды. Следовательно, уменьшится ее количество на выходе из трубы за тот же промежуток времени.

На производстве, при строительстве водопроводов составляются проекты, в которых высчитывается гидравлический расчет водопровода по уравнению Бернулли:

Где h 1-2 – показывает потерю напора на выходе, после преодоления сопротивления на всем участке водопровода.

Гидравлический расчет истечения жидкостей

Стенка считается тонкой, если ее толщина d стенки меньше двух диаметров отверстия do d < 2 do. В этом случае струя, вытекающая из отверстия, не касается стенок.

Стенка считается насадком (или толстой стенкой), если ее толщина больше двух диаметров отверстия d > 2 do. В этом случае струя, вытекающая из отверстия, касается стенок и занимает всё поперечное сечение.

Отверстие называется маленьким, если напор над центрам тяжести отверстия в больше одной десятой диаметра отверстия.

Отверстие называется большим, если напор над центрам тяжести отверстия в меньше одной десятой диаметра отверстия.

Истечение жидкости из малого отверстия в тонкой стенке

Рассмотрим вначале явление истечения капельной жидкости из круглого отверстия диаметром d в вертикальной тонкой стенке сосуда (рис.1). Давление в сосуде полагаем постоянным (движение установившееся) и равным p1 Истечение происходит в атмосферу, т.е. наружное давление равно pат; площадь отверстия wo, площадь сечения сосуда w1. Основные задачи, интересующие инженера, — определение скорости истечения и расхода вытекающей жидкости.

Как показывают опыты, струя жидкости по выходе из отверстия сжимается и на некотором расстоянии от последнего (обычно равным 0,5 диаметра струи) приобретает наименьшую площадь сечения wc (при диаметре dc). На рисунке 1 показаны линии токов, сходящиеся к отверстию в тонкой стенке.

Коэффициентом сжатия струи называется отношение площади поперечного сечения струи к площади поперечного сечения отверстия . (6.1) Коэффициентом сжатия струи зависит от отношения площади поперечного сечения отверстия к площади поперечного сечения потока до отверстия , (6.2) Который называется степенью сжатия струи n. Вид функции . (6.3) определяется формулами, которые были приведены в главе «Местные гидравлические сопротивления». Если площадь сечения отверстия wo мала по сравнению с площадью сечения сосуда отверстия (т.е. при n0, что соответствует случаю так называемого совершенного сжатия), формула Жуковского упрощается к виду . (6.4) Это так называемая формула Кирхгофа. В обычных условиях при истечении воды из малых отверстий в больших резервуарах опыт дает значения коэффициента сжатия струи, находящегося в пределах , (6.5) т.е. близкие к значению, определяемому формулой (6.5). Скорость истечения. Для определения скорости истечения напишем уравнение Бернулли для сечений 1-1 и c-c Рис. 6.2. Плоскость сравнения выберем проходящей через центр тяжести сжатого сечения. Абсолютные давления в сечениях p1 = pат + pм, pc = pат, значения геодезических отметок z1 = H, zc = 0, скорость в первом сечении равна нулю, а во втором сечении равна скорости сжатого сечения vc. Тогда уравнение Бернулли запишется: . (6.6) Потерями напора между сечениями являются только местное сопротивление на вход в отверстие, которое выражаются через коэффициент zвхо = 0,06. Поэтому последнее уравнение запишется: . (6.7) Поэтому скорость истечения будет равна (6.8) Рис. 6.26.2 схемы истечения жидкости Введем обозначение (6.9) где j — так называемый коэффициент скорости. В результате формула для скорости истечения принимает вид (6.10) При истечении воздуха или воды обычно (6.11) т.е. всего около 2-3% располагаемой разности давлений затрачивается на преодоление сопротивлений. Расход жидкости, выходящей из отверстия, находим по формуле (6.12) Подставляя вместо значения скорости в сжатом сечении, имеем (6.13) где m = e j — коэффициент расхода отверстия. В соответствии с формулой (17) коэффициент расхода отверстия представляет собой произведение коэффициента сжатия струи e на коэффициент скорости j. Значения m для разных n при истечении жидкости с большими числами Рейнольдса приведены в таблице 1. Таблица 6.1-Значение коэффициента расхода отверстия m при различной степени сжатия n n 0,611 0,5 0,678 0,1 0,614 0,6 0,74 0,2 0,622 0,7 0,787 0,3 0,634 0,8 0,888 0,4 0,65 0,9 1,09 При истечении из малых отверстий (n0) из формулы (17) имеем.

Кондиционеры

Кондиционеры и различные сплит-системы имеют определённый функционал (несколько режимов работы, двухканальную или одноканальную систему и так далее), благодаря которому эти устройства причисляются к тому или иному энергоклассу. Учитывается не только возможность охлаждения/кондиционирования воздуха, но и способность кондиционера нагревать обслуживаемое помещение.

Для определения класса энергоэффективности систему запускают на полную мощность на час. Коэффициент рассчитывается таким образом: охлаждающая или греющая производительность кондиционера делится на общую мощность прибора. Так, кондиционер А-класса должен иметь выходной показатель на уровне 3,2-3,4 (для функции охлаждения) или 3,6-3,8 (показатели для функции согревания воздуха).

Значение давления и скорости в потоке

Давление, которое обычно определяется, как сила на единицу площади, является важной характеристикой потока. Давление, оказываемое жидкостью, газом или паром в трубопроводе

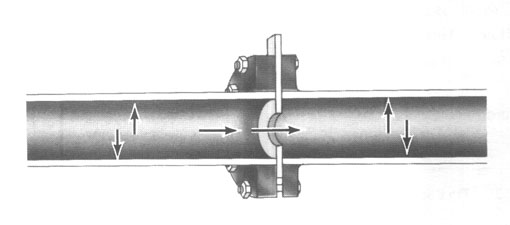Давление, оказываемое жидкостью, газом или паром в трубопроводе

На рисунке выше показаны два направления, в которых поток жидкости, газа или пара, двигаясь, оказывает давление в трубопроводе в направлении самого потока и на стенки трубопровода. Именно давление во втором направлении чаще всего используют в расходомерных устройствах, в которых на основе показания перепада давления в трубопроводе, определяется расход.

Скорость, с которой течет жидкость, газ или пар в значительной степени влияет на величину давления, оказываемого жидкостью, газом или паром на стенки трубопровода; в результате изменения скорости изменится давление на стенки трубопровода. На рисунке ниже графически изображена взаимосвязь между скоростью потока жидкости, газа или пара и давлением, которое оказывает поток жидкости на стенки трубопровода.

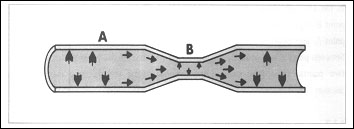Взаимосвязь между скоростью и давлением

Как видно из рисунка, диаметр трубы в точке «А» больше, чем диаметр трубы в точке «B». Так как количество жидкости, входящей в трубопровод в точке «А», должно равняться количеству жидкости, выходящей из трубопровода в точке «В», скорость, с которой течёт жидкость, проходя более узкую часть трубы, должна увеличиваться. При увеличении скорости жидкости, будет уменьшаться давление, оказываемое жидкостью на стенки трубы.

Для того, чтобы показать, как увеличение скорости расхода текучей среды может приводить к уменьшению величины давления, оказываемого потоком текучей среды на стенки трубопровода, можно воспользоваться математической формулой. В этой формуле учтены только скорость и давление. Другие показатели, такие как: трение или вязкость не учтены

Если не принимать во внимание эти показатели, то упрощенная формула записывается так: PA + K (VA)2 = PB + K (VB)2

Давление, оказываемое текучей средой на стенки трубы, обозначено буквой P. РA — это давление на стенки трубопровода в точке «А» и PB — это давление в точке «B». Скорость текучей среды обозначена буквой V. VA — это скорость текучей среды по трубопроводу в точке «А» и VB — это скорость в точке «B». K — это математическая константа.

Как уже было сформулировано выше, для того, чтобы количество газа, жидкости или пара прошедшее трубопровод в точке «B», равнялось количеству газа, жидкости или пара, вошедшему в трубопровод в точке «А», скорость жидкости, газа или пара в точке «B» должна увеличиваться. Поэтому, если PA + K (VA)2 должно равняться PB + K (VB)2, то при увеличении скорости VB давление РB должно уменьшиться. Таким образом увеличение скорости приводит к уменьшению параметра давления.

Полезное определение

Объемный расход также можно определить по:

Q=v⋅А{ Displaystyle Q = mathbf {v} cdot mathbf {A}}

куда:

• v = скорость потока
• А = поперечный векторная площадь /поверхность

Вышеприведенное уравнение справедливо только для плоских сечений. В общем, включая криволинейные поверхности, уравнение становится поверхностный интеграл:

Q=∬Аv⋅dА{ Displaystyle Q = iint _ {A} mathbf {v} cdot mathrm {d} mathbf {A}}

Это определение используется на практике. В площадь Требуемый для расчета объемный расход реальный или мнимый, плоский или криволинейный, как площадь поперечного сечения или поверхность. В векторная площадь представляет собой комбинацию величины площади, через которую проходит объем, А, а единичный вектор нормально к области, n. Отношение А = Аn.

Причина скалярное произведение как следует. Единственный объемный поток через поперечное сечение — это величина, нормальная к площади, то есть параллельно к агрегату нормальный. Эта сумма составляет:

Q=vАпотому что⁡θ{ Displaystyle Q = vA соз тета}

куда θ угол между нормалью единицы n и вектор скорости v элементов вещества. Количество проходящих через поперечное сечение уменьшается в раз. потому что θ. В качестве θ увеличивается меньше объем проходит. Вещество, которое проходит по касательной к области, то есть перпендикуляр к агрегату нормальный, по площади не проходит. Это происходит, когда θ = π2 и поэтому эта величина объемного расхода равна нулю:

Q=vАпотому что⁡(π2)={ displaystyle Q = vA cos left ({ frac { pi} {2}} right) = 0}

Эти результаты эквивалентны скалярному произведению между скоростью и нормальным направлением к области.

Когда массовый расход известно, и плотность можно считать постоянной, это простой способ получить Q{ displaystyle Q}.

Q=м˙ρ{ displaystyle Q = { frac { dot {m}} { rho}}}

Где:

• ṁ = массовый расход (в кг / с).
• ρ = плотность (в кг / м3).

Стиральные машинки

Расчёт энергетической эффективности осуществляется специалистами в соответствующей экспертной организации на основе сразу нескольких параметров для каждого отдельного вида (артикула) прибора в зависимости от их размеров, мощности, функционала. Так, для электрической стиральной машинки важными при определении энергокласса является показатель мощности, которая потребляется за час работы, качество стирки и количество стираемого за один раз белья.

Если при вычислении энергопотребления машинки для стирки одного килограмма белья используется минимум 0,17, максимум 0,19 киловатт в час, это прибор можно относить к А-классу. Следующий класс А+ стиральной машины отличается тем, что потребляет от 0,15 до 0,17 киловатт в час для однокилограммовой загрузки (при расчёте необходимо делать поправку на максимальное количество килограмм грязного белья, которое может обработать машинка за один раз). Наличие на этикетке (в паспорте) стиральной техники сразу нескольких букв, обозначает разные классы энергоэффективности для различных процессов – для непосредственно стирки, для отжима, для сушки.

Проверка эффективности стиральных машин осуществляется следующим образом. Берут два одинаковых чистых куска материи, один из них загрязняют и отправляют в стирку при температуре в 60 градусов по шкале Цельсия на час. После этого сравнивается эталонный и выстиранный кусок ткани и оценивается, насколько хорошо отстирались пятна и каково было потребление электрического тока.

Поток жидкости и его параметры

Поток жидкости характеризуется такими параметрами как площадь живого сечения S, расход жидкости Q(G), средняя скорость движения v.

Живое сечение потока — это сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.

Векторы скорости частиц имеют некоторое расхождение в потоке жидкости.

Живым сечением потока жидкости называется сечение, которое перпендикулярно в каждой точке скорости частиц потока жидкости.

Поэтому живое сечение потока — криволинейная плоскость (рис. а, линия I—I) В виду незначительного расхождения векторов скорости в гидродинамике за живое сечение принимается плоскость, расположенная перпендикулярно скорости движения жидкости в средней точке потока.

Расход жидкости — это количество жидкости, протекающей через живое сечение потока в единицу времени. Расход может определяться в массовых долях G и объемных Q.

Средняя скорость движения жидкости — это средняя скорость частиц в живом сечении потока.

Если в живом сечении потока, движущегося, например, в трубе, построить векторы скорости частиц и соединить концы этих векторов, то получится график изменения скоростей (эпюра скоростей).

Если площадь такой эпюры разделить на диаметр данной трубы, то получится значение средней скорости движения жидкости в данном сечении:

Объемный расход жидкости рассчитывается по формуле:

Параметры потока жидкости определяют характер движения жидкости. При этом оно может быть установившимся и неустановившимся, равномерным и неравномерным, неразрывным и кавитационным, ламинарным и турбулентным.

Если параметры потока жидкости не изменяются во времени, то ее движение называется установившимся.

Равномерным называется движение, при котором параметры потока не изменяются по длине трубопровода или канала. Например, движение жидкости по трубе постоянного диаметра является равномерным.

Неразрывным называется движение жидкости, при котором она перемещается сплошным потоком, заполняющим весь объем трубопровода.

Отрыв потока от стенок трубопровода или от обтекаемого предмета приводит к возникновению кавитации.

Кавитацией называется образование в жидкости пустот, заполненных газом, паром или их смесью.

Кавитация возникает в результате местного уменьшения давления ниже критического значения pкр при данной температуре (для воды ркр= 101,3 кПа при Т= 373 К или ркр= 12,18 кПа при Т= 323 К и т. д.). При попадании таких пузырьков в зону, где давление выше критического, в эти пустоты устремляются частицы жидкости, что приводит к резкому возрастанию давления и температуры. Поэтому кавитация неблагоприятно отражается на работе гидротурбин, жидкостных насосов и других элементов гидравлических устройств.

Ламинарное движение — это упорядоченное движение жидкости без перемешивания между ее соседними слоями. При ламинарном течении скорость и силы инерции, как правило, невелики, а силы трения значительны. При увеличении скорости до некоторого порогового значения ламинарный режим течения переходит в турбулентный.

Турбулентное движение — это течение жидкости, при котором ее частицы совершают неустановившееся беспорядочное движение по сложным траекториям. При турбулентном течении скорость жидкости и ее давление в каждой точке потока хаотически изменяется, при этом происходит интенсивное перемешивание движущейся жидкости.

Для определения режима движения жидкости существуют условия, согласно которым скорость потока может быть больше или меньше той критической скорости, когда ламинарное движение переходит в турбулентное и наоборот.

Однако установлен и более универсальный критерий, который называют критерием или числом Рейнольдса:

Опытами было установлено, что в момент перехода ламинарного режима движения жидкости в турбулентный Re = 2320.

Число Рейнольдса, при котором ламинарный режим переходит в турбулентный, называется критическим. Следовательно, при Re 2320 — турбулентное. Отсюда критическая скорость для любой жидкости:

Источник

Таблица единиц измерения «Механика»

Физическая величина	Символ	Единица измерения физической величины	Ед. изм. физ. вел.	Описание	Примечания
Масса	m	килограмм	кг	Величина, определяющая инерционные и гравитационные свойства тел.	экстенсивная величина
Плотность	ρ	килограмм на кубический метр	кг/м3	Масса на единицу объёма.	интенсивная величина
Поверхностная плотность	ρA	Масса на единицу площади.	кг/м2	Отношение массы тела к площади его поверхности
Линейная плотность	ρl	Масса на единицу длины.	кг/м	Отношение массы тела к его линейному параметру
Удельный объем	v	кубический метр на килограмм	м3/кг	Объём, занимаемый единицей массы вещества
Массовый расход	Qm	килограмм в секунду	кг/с	Масса вещества, которая проходит через заданную площадь поперечного сечения потока за единицу времени
Объемный расход	Qv	кубический метр в секунду	м3/с	Объёмный расход жидкости или газа
Импульс	P	килограмм-метр в секунду	кг•м/с	Произведение массы и скорости тела.	экстенсивная, сохраняющаяся величина
Момент импульса	L	килограмм-метр в квадрате в секунду	кг•м2/с	Мера вращения объекта.	сохраняющаяся величина
Момент инерции	J	килограмм-метр в квадрате	кг•м2	Мера инертности объекта при вращении.	тензорная величина
Сила, вес	F, Q	ньютон	Н	Действующая на объект внешняя причина ускорения.	вектор
Момент силы	M	ньютон-метр	Н•м = (кг·м2/с2)	Произведение силы на длину перпендикуляра, опущенного из точки на линию действия силы.	вектор
Импульс силы	I	ньютон-секунда	Н•с	Произведение силы на время её действия	вектор
Давление, механическое напряжение	p, σ	паскаль	Па = (кг/(м·с2))	Сила, приходящаяся на единицу площади.	интенсивная величина
Работа	A	джоуль	Дж = (кг·м2/с2)	Скалярное произведение силы и перемещения.	скаляр
Энергия	E, U	джоуль	Дж = (кг·м2/с2)	Способность тела или системы совершать работу.	экстенсивная, сохраняющаяся величина, скаляр
Мощность	N	ватт	Вт = (кг·м2/с3)	Скорость изменения энергии.