Перевод объемного расхода в массовый и обратно

США и Британия

В виду того, что в некоторых англоязычных странах объем измеряется в отличных от системы СИ единицах, переводим их в систему СИ.

• 1 дюйм = 0.0254 м. Тогда кубический дюйм = 0.000016387064 м³ (точно)
• 1 фут = 0.3048 м. Тогда кубический фут = 0.028316846592 м³ (точно)
• 1 ярд = 0.9144 м. Тогда кубический ярд = 0.764554857984 м³ (точно)
• 1 акр = 4840 квадратных ярдов = 4046.8564224 м² (точно)
• Акр-фут — объем воды, необходимый для покрытия высотой в один фут площади в один акр.
    Тогда 1 акр-фут = 1233.48183754752 м³ (точно)
• 1 баррель (американский, нефтяной) = 0.158988 м³
• 1 американский галлон = 0.003785411784 м³
• 1 имперский (британский) галлон = 0.00454609188 м³
• Принимаем: 1 год = 365.25 суток

И тогда рассчитываем:

• 1 акр-фут в секунду [af/s] = 1233.48183754752 метр³ в секунду [м³/с] (точно)
• 1 акр-фут в минуту [af/min] = 20.55803062579 метр³ в секунду [м³/с] (точно)
• 1 акр-фут в час [af/h] = 0.34263384376 метр³ в секунду [м³/с] (точно)
• 1 акр-фут в сутки [af/d] = 51.39507656448 метр³ в час [м³/ч] (точно)
• 1 акр-фут в год [af/yr] = 0.14071205083 метр³ в час [м³/ч] (точно)
• 1 баррель (нефть) в секунду [bbl/s] = 0.158988 метр³ в секунду [м³/с]
• 1 баррель (нефть) в минуту [bbl/min] = 9.53928 метр³ в час [м³/ч]
• 1 баррель (нефть) в час [bbl/h] = 3.815712 метр³ в сутки [м³/сут]
• 1 баррель (нефть) в сутки [bbl/d] = 58.070367 метр³ в год [м³/г]
• 1 баррель (нефть) в год [bbl/yr] = 158.988 литров в год [л/г]
• 1 галлон (US) в секунду = 3.785411784 литров в секунду [л/с]
• 1 галлон (US) в минуту = 0.0630901964 литров в секунду [л/с]
• 1 галлон (US) в час = 3.785411784 литров в час [л/ч]
• 1 галлон (US) в сутки = 3.785411784 литров в сутки [л/сут]
• 1 галлон (US) в год = 3.785411784 литров в год [л/г]
• 1 фут³ в секунду [ft³/s] = 1728 [in³/s] = 28.316846592 литров в секунду [л/с] (точно)
• 1 фут³ в минуту [ft³/min] = 28.8 [in³/s] = 0.4719474432 литров в секунду [л/с] (точно)
• 1 фут³ в час [ft³/h] = 0.46 [in³/s] = 28.316846592 литров в час [л/ч] (точно)
• 1 фут³ в сутки [ft³/d] = 0.02 [in³/s] = 1.179868608 литров в час [л/ч] (точно)
• 1 фут³ в год [ft³/yr] = 1728 [in³/yr] = 28.316846592 литров в год [л/г] (точно)
• 1 дюйм³ в секунду [in³/s] = 0.0005787037 [ft³/s] = 58.9934304 литров в час [л/ч] (точно)
• 1 дюйм³ в минуту [in³/min] = 0.0005787037 [ft³/min] = 0.98322384 литров в час [л/ч] (точно)
• 1 дюйм³ в час [in³/h] = 0.0005787037 [ft³/h] = 0.393289536 литров в сутки [л/сут] (точно)
• 1 дюйм³ в сутки [in³/d] = 0.0005787037 [ft³/d] = 5.985375126 литров в год [л/г] (точно)
• 1 дюйм³ в год [in³/yr] = 0.0005787037 [ft³/yr] = 0.016387064 литров в год [л/г] (точно)

Основное определение

Объемный расход определяется предел:

Q=V˙=LimΔт→ΔVΔт=dVdт{ displaystyle Q = { dot {V}} = lim limits _ { Delta t rightarrow 0} { frac { Delta V} { Delta t}} = { frac { mathrm {d} V} { mathrm {d} t}}}

То есть поток объем жидкости V через поверхность в единицу времени т.

Поскольку это только производная по времени от объема, скалярная величина, объемный расход также является скалярной величиной. Изменение объема — это количество, которое течет после пересечение границы в течение некоторого времени, а не просто начальное количество объема на границе минус конечное количество на границе, поскольку изменение объема, протекающего через область, будет равно нулю для устойчивого потока.

Значение давления и скорости в потоке

Давление, которое обычно определяется, как сила на единицу площади, является важной характеристикой потока. Давление, оказываемое жидкостью, газом или паром в трубопроводе

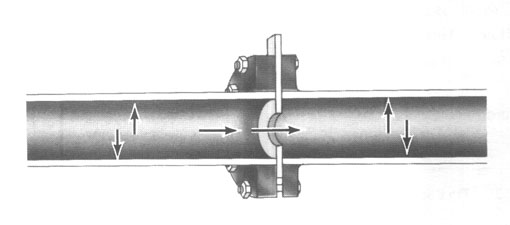Давление, оказываемое жидкостью, газом или паром в трубопроводе

На рисунке выше показаны два направления, в которых поток жидкости, газа или пара, двигаясь, оказывает давление в трубопроводе в направлении самого потока и на стенки трубопровода. Именно давление во втором направлении чаще всего используют в расходомерных устройствах, в которых на основе показания перепада давления в трубопроводе, определяется расход.

Скорость, с которой течет жидкость, газ или пар в значительной степени влияет на величину давления, оказываемого жидкостью, газом или паром на стенки трубопровода; в результате изменения скорости изменится давление на стенки трубопровода. На рисунке ниже графически изображена взаимосвязь между скоростью потока жидкости, газа или пара и давлением, которое оказывает поток жидкости на стенки трубопровода.

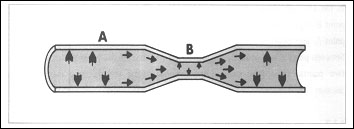Взаимосвязь между скоростью и давлением

Как видно из рисунка, диаметр трубы в точке «А» больше, чем диаметр трубы в точке «B». Так как количество жидкости, входящей в трубопровод в точке «А», должно равняться количеству жидкости, выходящей из трубопровода в точке «В», скорость, с которой течёт жидкость, проходя более узкую часть трубы, должна увеличиваться. При увеличении скорости жидкости, будет уменьшаться давление, оказываемое жидкостью на стенки трубы.

Для того, чтобы показать, как увеличение скорости расхода текучей среды может приводить к уменьшению величины давления, оказываемого потоком текучей среды на стенки трубопровода, можно воспользоваться математической формулой. В этой формуле учтены только скорость и давление. Другие показатели, такие как: трение или вязкость не учтены

Если не принимать во внимание эти показатели, то упрощенная формула записывается так: PA + K (VA)2 = PB + K (VB)2

Давление, оказываемое текучей средой на стенки трубы, обозначено буквой P. РA — это давление на стенки трубопровода в точке «А» и PB — это давление в точке «B». Скорость текучей среды обозначена буквой V. VA — это скорость текучей среды по трубопроводу в точке «А» и VB — это скорость в точке «B». K — это математическая константа.

Как уже было сформулировано выше, для того, чтобы количество газа, жидкости или пара прошедшее трубопровод в точке «B», равнялось количеству газа, жидкости или пара, вошедшему в трубопровод в точке «А», скорость жидкости, газа или пара в точке «B» должна увеличиваться. Поэтому, если PA + K (VA)2 должно равняться PB + K (VB)2, то при увеличении скорости VB давление РB должно уменьшиться. Таким образом увеличение скорости приводит к уменьшению параметра давления.

Связанные количества

В двигателях внутреннего сгорания интеграл по времени учитывается по диапазону открытия клапана. Интеграл временного лифта определяется как:

∫Ldθ=рТ2π(потому что⁡θ2−потому что⁡θ1)+рТ2π(θ2−θ1){ displaystyle int L , mathrm {d} theta = { frac {RT} {2 pi}} left ( cos theta _ {2} — cos theta _ {1} right ) + { frac {rT} {2 pi}} left ( theta _ {2} — theta _ {1} right)}

куда Т время на оборот, р расстояние от осевой линии распределительного вала до конца кулачка, р — радиус распредвала (то есть р − р максимальный подъем), θ₁ это угол, где начинается открытие, и θ₂ где закрывается клапан (секунды, мм, радианы). Это должно учитываться шириной (окружностью) горловины клапана. Ответ обычно связан с рабочим объемом цилиндра.

Технические расчеты бесплатно и анонимно =)

• Отопление
  • Расчет тепловой нагрузки по укрупненным показателям МДК 4-05.2004
  • Расчет диаметра коллектора
  • Расчет расширительного бака для отопления
  • Расчет количества ступеней теплообменника ГВС
  • Расчет нагрева ГВС
  • Расчет длины компенсаторов температурных удлинений трубопроводов
  • Расчет скорости воды в трубопроводе
  • Разбавление пропилен и этиленгликоля
  • Расчет диаметра балансировочной шайбы
  • Проверка работоспособности элеваторной системы отопления
  • кг/с в м3/ч. Перевод массового расхода среды в объемный.
  • Онлайн замена радиаторов Prado на Purmo
  • Примеры гидравлических расчетов систем отопления
  • Sanext
    • Расчет диаметра и настройки клапана Sanext DPV
    • Расчет этажного коллектора системы отопления Sanext
    • Маркировка РКУ Sanext
    • Замена клапана Danfoss AB-QM на Sanext DS
    • Быстрая замена L и T-образных трубок на трубу Стабил
• Вентиляция
  • Расчет гравитационного давления
  • Расчет расхода воздуха на удаление теплоизбытков
  • Расчет теплоснабжения приточных установок
  • Расчет осушения помещений по методике Dantherm
  • Расчет эквивалентного диаметра и скорости воздуха в воздуховоде
  • Расчет дымоудаления с естественным побуждением
  • Расчет площади воздуховодов и фасонных частей онлайн
  • Расчет естественной вентиляции онлайн
  • Расчет потерь давления на местных сопротивлениях
  • Расчет воздушного отопления совмещенного с вентиляцией
  • Расчет вентиляции в аккумуляторной
  • Расчет температуры приточного и вытяжного воздуха системы вентиляции
  • Расчет углового коэффициента луча процесса
  • Кратности воздухообмена и температуры воздуха
  • Расчет количества облучателей-рециркуляторов медицинских по Р 3.5.1904-04
• Кондиционирование
  • Расчет мощности кондиционера по теплопритокам в помещение
  • Расчет теплопритоков от солнечной радиации. Инсоляция помещения.
  • Расчет теплопоступлений от источников искусственного освещения
  • Расчет теплопоступлений от оборудования
  • Расчет теплопоступлений от людей
  • Расчет теплопритоков и влаги от остывающей еды
  • Расчет теплопоступлений от инфильтрации воздуха
  • Расчет полной теплоты из явной теплоты
• Водоснабжение
  • Расчет сопротивления в трубопроводе ВК
  • Расчет глубины промерзания грунта
  • Расчетные расходы дождевых вод
• Газоснабжение
  • Технико-экономический расчет тепла и топлива
  • Расчет диаметра газопровода
  • Расчет теплотворной способности энергоносителей
• Смета
  • Расчет площади окраски металлического профиля
  • Расчет площади окраски чугунных радиаторов
  • Расчет расхода теплоизоляции с учетом коэффициента уплотнения
  • Расчет количества досок из кубометра древесины
  • Примеры смет
    • Пример сметы на авторский надзор
    • Пример сметы на перебазирование техники
    • Пример расчета коэффициента к ФОТ при сверхурочной работе.
    • Пример расчета коэффициента к ФОТ при многосменном режиме работы.
    • Пример расчета коэффициента к ФОТ при вахтовом методе работы.
    • Списание материалов в строительстве. Пример формы отчета.
    • Списание материалов в строительстве. Пример формы ведомости.
• Разные
  • Конвертер технических величин
  • Проверка показаний теплосчетчика онлайн
  • Расчет категории склада для хранения муки
  • Линейная интерполяция онлайн
  • Онлайн расчет маржинальности и точки безубыточности
  • НДС калькулятор онлайн, расчет %
  • Юнит-экономика онлайн калькулятор
  • Расчет стоимости покупки автомобиля по доходу семьи
  • Расчет стоимости системы учета энергоресурсов
  • Калькулятор технологии домашнего виноделия
  • На всю котлету
  • Закон Ома
  • Расчет фундамента
  • Статьи
    • Нормы
    • Сравнение типов отопительных приборов
    • Настройка AutoCAD
    • Температура воздуха в Краснодаре за 10 лет зимой
    • Сравнение ИП с ООО
• Вход

Альтернативные уравнения [ править ]

Иллюстрация объемного расхода. Массовый расход можно рассчитать, умножив объемный расход на массовую плотность жидкости ρ . Объемный расход вычисляется путем умножения скорости потока масс элементов, V , с помощью поперечного сечения векторной области, A .

Массовый расход также можно рассчитать с помощью:

м˙знак равноρ⋅V˙знак равноρ⋅v⋅Азнак равноjм⋅А{\ displaystyle {\ dot {m}} = \ rho \ cdot {\ dot {V}} = \ rho \ cdot \ mathbf {v} \ cdot \ mathbf {A} = \ mathbf {j} _ {\ rm { м}} \ cdot \ mathbf {A}}

куда:

• V˙{\ displaystyle {\ dot {V}}}или Q = объемный расход ,
• ρ = массовая плотность жидкости,
• v = скорость потока массовых элементов,
• A = площадь вектора поперечного сечения / поверхность,
• j _m = массовый поток .

Вышеприведенное уравнение справедливо только для плоского плоского участка. В общем, включая случаи, когда область изогнута, уравнение становится поверхностным интегралом

м˙знак равно∬Аρv⋅dАзнак равно∬Аjм⋅dА{\ displaystyle {\ dot {m}} = \ iint _ {A} \ rho \ mathbf {v} \ cdot {\ rm {d}} \ mathbf {A} = \ iint _ {A} \ mathbf {j} _ {\ rm {m}} \ cdot {\ rm {d}} \ mathbf {A}}

Площадь , необходимая для вычисления массового расход является реальным или мнимым, плоским или изогнутым, либо как площадь поперечного сечения или поверхность, например , для веществ , проходящих через фильтр или мембрану , реальная поверхностью является (обычно изогнуто) поверхностью площадь фильтра, макроскопически — игнорируя площадь, охватываемую отверстиями в фильтре / мембране. Пространства будут площадями поперечного сечения. Для жидкостей, проходящих через трубу, площадь представляет собой поперечное сечение трубы в рассматриваемом сечении. Вектор площадь представляет собой комбинацию величины площади , через которую проходит через массу, A , и единичного вектора нормали к области,п^{\ Displaystyle \ mathbf {\ шляпа {п}}}. Отношение такое .Азнак равноАп^{\displaystyle \mathbf {A} =A\mathbf {\hat {n}} }

Причина скалярного произведения заключается в следующем. Единственная масса, протекающая через поперечное сечение, — это величина, нормальная к площади, то есть параллельная единице нормали. Эта сумма составляет:

m˙=ρvAcos⁡θ{\displaystyle {\dot {m}}=\rho vA\cos \theta }

где θ — угол между нормалью единицы и скоростью массовых элементов. Количество проходящих через поперечное сечение уменьшается в раз , поскольку θ увеличивается, меньше массы проходит через. Вся масса, которая проходит по касательной к области, перпендикулярной единице нормали, на самом деле не проходит через область, поэтому масса, проходящая через область, равна нулю. Это происходит, когда θ = π / 2:n^{\displaystyle \mathbf {\hat {n}} }cos⁡θ{\displaystyle \cos \theta }

m˙=ρvAcos⁡(π2)={\displaystyle {\dot {m}}=\rho vA\cos(\pi /2)=0}

Эти результаты эквивалентны уравнению, содержащему скалярное произведение. Иногда эти уравнения используются для определения массового расхода.

Учитывая поток через пористую среду, можно ввести особую величину — поверхностный массовый расход. Это связано с поверхностной скоростью , v _s , со следующим соотношением:

m˙s=vs⋅ρ=m˙A{\displaystyle {\dot {m}}_{s}=v_{s}\cdot \rho ={\dot {m}}/A}

Величина может использоваться при расчете или коэффициента массопереноса для систем с неподвижным и псевдоожиженным слоем.

Рекомендации

Гидромеханика, М. Поттер, округ Колумбия Виггарт, наброски Шуама, Макгроу Хилл (США), 2008, ISBN  978-0-07-148781-8

Линдебург М. Р. Справочное руководство по химической инженерии для экзамена PE. — Professional Publications (CA), 2013.

Основные принципы физики, П.М. Уилан, М.Дж. Ходжсон, 2-е издание, 1978, Джон Мюррей, ISBN  0-7195-3382-1

^ Холлидей; Резник. Физика. 1. п. 199. ISBN  978-0-471-03710-1

Важно отметить, что мы не можешь получить общее выражение для второго закона Ньютона для систем с переменной массой, рассматривая массу в F = dп/dt = d(Mv) как Переменная. Мы может использовать F = dп/dt для анализа систем переменной массы Только если мы применим его к вся система постоянной массы части, между которыми происходит обмен массой

Ченгель, Юнус А. (2002). Термодинамика: инженерный подход. Болес, Майкл А. (4-е изд.). Бостон: Макгроу-Хилл. ISBN  0-07-238332-1. OCLC  .

Горовиц, Пол, 1942- (30 марта 2015 г.). Искусство электроники. Хилл, Уинфилд (Третье изд.). Нью-Йорк, штат Нью-Йорк, США. ISBN  978-0-521-80926-9. OCLC  .

Международная система единиц (СИ)

Для международной системы единиц (СИ), подставляя в вышеприведенную формулу расхода значения объема в , а время в секундах , получаем что единицей объемного расхода в СИ является 1 м³/сек.
  Приводим список производных от нее величин:

• 1 метр³ в секунду [м³/с] = 60 метр³ в минуту [м³/мин]
• 1 метр³ в минуту [м³/мин] = 60 метр³ в час [м³/ч]
• 1 метр³ в час [м³/ч] = 24 метр³ в сутки [м³/сут]
• 1 метр³ в сутки [м³/сут] = 365.25 метр³ в год [м³/г]
• 1 метр³ в секунду [м³/с] = 1000 литров в секунду [л/с]
• 1 литр в секунду [л/с] = 60 литров в минуту [л/мин]
• 1 литр в минуту [л/мин] = 60 литров в час [л/ч]
• 1 литр в час [л/ч] = 24 литров в сутки [л/сут]
• 1 литр в сутки [л/сут] = 365.25 литров в год [л/г]