Средняя скорость

Основные понятия и законы кинематики

кинематикойМеханическим движениемСистемой отсчётаТелом отсчётаМатериальной точкойТраекториейпрямолинейноекриволинейноеПуть — это длина траектории, которую описывает материальная точка за данный промежуток времени. Это скалярная величина.Перемещение — это вектор, соединяющий начальное положение материальной точки с её конечным положением (см. рис.).

Очень важно понимать, чем путь отличается от перемещения. Самое главной отличие в том, что перемещение — это вектор с началом в точке отправления и с концом в точке назначения (при этом абсолютно неважно, каким маршрутом это перемещение совершалось). А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории

А путь — это, наборот, скалярная величина, отражающая длину пройденной траектории.

Равномерным прямолинейным движением называют движение, при котором материальная точка за любые равные промежутки времени совершает одинаковые перемещенияСкоростью равномерного прямолинейного движения называют отношение перемещения ко времени, за которое это перемещение произошло:

Для неравномерного движения пользуются понятием средней скорости. Часто вводят среднюю скорость как скалярную величину. Это скорость такого равномерного движения, при котором тело проходит тот же путь за то же время, что и при неравномерном движении:

Мгновенной скоростью называют скорость тела в данной точке траектории или в данный момент времени.Равноускоренное прямолинейное движение — это прямолинейное движение, при котором мгновенная скорость за любые равные промежутки времени изменяется на одну и ту же величину

Ускорением

Зависимость координаты тела от времени в равномерном прямолинейном движении имеет вид: x = x + V_xt, где x — начальная координата тела, V_x — скорость движения.Свободным падением называют равноускоренное движение с постоянным ускорением g = 9,8 м/с2, не зависящим от массы падающего тела. Оно происходит только под действием силы тяжести.

Скорость при свободном падении рассчитывается по формуле:
Перемещение по вертикали рассчитывается по формуле:

Одним из видов движения материальной точки является движение по окружности. При таком движении скорость тела направлена по касательной, проведённой к окружности в той точке, где находится тело (линейная скорость). Описывать положение тела на окружности можно с помощью радиуса, проведённого из центра окружности к телу. Перемещение тела при движении по окружности описывается поворотом радиуса окружности, соединяющего центр окружности с телом. Отношение угла поворота радиуса к промежутку времени, в течение которого этот поворот произошёл, характеризует быстроту перемещения тела по окружности и носит название угловой скорости
ω:
Угловая скорость связана с линейной скоростью соотношением где r — радиус окружности.
Время, за которое тело описывает полный оборот, называется периодом обращения. Величина, обратная периоду — частота обращения — ν
Поскольку при равномерном движении по окружности модуль скорости не меняется, но меняется направление скорости, при таком движении существует ускорение. Его называют центростремительным ускорением, оно направлено по радиусу к центру окружности:

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

t = S: V

15: 3 = 5 (с)

Составим выражение: 5 3: 3 = 5 (с) Ответ: 5 с потребуется слепню.

Реши задачу.

1. Катер, двигаясь со скоростью 32 км/ч, про­шёл путь между пристанями за 2 ч. Сколько потребуется времени, чтобы пройти этот же путь на лодке, если она движется со скорос­тью 8 км/ч?

2.Велосипедист, двигаясь со скоростью 10 км/ч, проехал путь между деревнями за 4 ч. Сколько

потребуется времени пешеходу, чтобы пройти этот же путь, если он движется со скоростью 15 км/ч?

Составные задачи на время. II тип.

Образец:

Многоножка сначала бежала 3 мин со скоростью 2 дм/м, а потом она побежала со скоростью 3 дм/м. За какое время мно­гоножка пробежала оставшийся путь, если всего она пробежала 15 дм? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.

Скорость (V) Время (t) Расстояние (S)

С. — 2 дм/мин З мин?дм

П.-3 дм/мин? ? мин?дм 15дм

Составим план решения этой задачи. Что­бы узнать, время многоножки потом, надо узнать какое расстояние она пробежала потом, а для этого надо знать, какое рас­стояние она пробежала сначала.

t п S п S с

S с = V с · t

2 3 = 6 (м) — расстояние, которое пробе­жала многоножка сначала.

S п = S — S с

15 — 6 = 9 (м) — расстояние, которое пробежала многоножка потом.

Чтобы найти время, надо расстояние раз­делить на скорость.

9: 3 = 3(мин)

Ответ: за 3 мин многоножка пробежала оставшийся путь.

Реши задачу.

1. Волк бежал по лесу 3 ч со скоростью 8 км/ч. По полю он бежал со скоростью 10 км/ч. Сколько времени волк бежал по полю, если он пробежал 44 км?

2. Рак до коряги полз 3 мин со скоростью 18 м/мин. Остальной путь он полз со скоростью 16 м/мин. Сколько времени потребовалось раку на остальной путь, если он прополз 118м?

3. Гена добежал до футбольной площадки за 48 с со скоростью 6 м/с, а потом он побежал к школе со скоростью 7 м/с. Через какое время Гена добежит до школы, если он пробежал 477 м?

4. Пешеход шёл до остановки 3 ч со скоростью 5 км/ч, после остановки он пошёл со скорос­тью 4 км/ч. Сколько времени пешеход был в пути после остановки, если он прошёл 23км?

5. Уж плыл до коряги 10с со скоростью 8 дм/с, а потом он поплыл до берега со скоростью 6 дм/с. За какое время доплыл уж до берега, если он проплыл 122дм?

Составные задачи на скорость. I тип

Образец:

Из норки побежали два ёжика. Один бе­жал 6 с со скоростью 2 м/с. С какой ско­ростью должен бежать другой ёжик, чтобы преодолеть это расстояние за 3 с? Рассуждаем так. Это задача на движение в одном направлении. Составим таблицу. Слова «скорость», «время», «расстояние» запишем в таблице зелёной ручкой.

Скорость (V) Время (1) Расстояние (8)

I — 2 м/с 6 с одинаковое

II — ?м/с 3 с

Составим план решения этой задачи. Что­бы найти скорость второго ёжика, надо найти расстояние, которое пробежал пер­вый ёжик.

Чтобы найти расстояние, надо скорость умножить на время.

S = V I · t I

2 · 6 = 12 (м) – расстояние, которое пробежал первый ежик.

Чтобы найти скорость, надо расстояние разделить на время.

V II = S: t II

12:3 = 4(м/с)

Составим выражение: 2 6:3 = 4 (м/с)

Ответ; 4м/с скорость второго ёжика.

Реши задачу.

1. Один кальмар плыл 4 с со скоростью 10 м/с. С какой скоростью должен плыть другой кальмар, чтобы преодолеть это расстояние за 5 с?

2. Трактор, двигаясь со скоростью 9 км/ч, прошёл путь между деревнями за 2 ч. С какой скоростью должен идти пешеход, чтобы пре­одолеть это расстояние за 3 ч?

3. Автобус, двигаясь со скоростью 64 км/ч, про­шёл путь между городами за 2 ч. С какой скоростью должен ехать велосипедист, что­бы преодолеть это расстояние за 8 ч?

4. Чёрный стриж летел 4 мин со скоростью 3 км/мин. С какой скоростью должна лететь утка кряква, чтобы преодолеть это расстоя­ние за 6 мин?

Составные задачи на скорость. II тип

Лыжник до горки ехал 2 ч со скоростью 15 км/ч, а потом по лесу он ехал ещё 3 ч. С какой скоростью лыжник будет ехать по лесу, если всего он проехал 66км?

В этом уроке мы рассмотрим три физические величины, а именно расстояние, скорость и время.

Содержание урока

Средняя скорость — машина

Средняя скорость машин ЕС-1030 по Гибсону составляет 100 тыс. операций в секунду.
 

Под средней скоростью машины понимают среднюю линейную скорость одной из точек ведущего вала машины во время ее установившегося движения.
 

Для того чтобы средняя скорость машины могла оставаться постоянной, необходимо, чтобы при этой скорости имело место равновесие между работой движущих сил и работой сопротивлений. Но это равновесие может нарушаться по различным причинам.
 

Для установления козфициента нагрузки двигателя определим среднюю скорость машины v — кгк, момент трения по формуле ( 55), угловую скорость машины ( см. фиг.
 

Очевидно, что такая система позволяет на уровне программирования заботиться о том, чтобы информация была заранее считана в быстрые регистры операндов и арифметическое устройство не ожидало ее поступления из памяти. Средняя скорость машины CDC-6600 оценивается в 3 5 млн. операций в секунду, однако, как утверждают разработчики, при оптимальном программировании она может быть значительно повышена.
 

Сравнение формул ( 52) и ( 58) дает следующий вывод: коэфициент нагрузки двигателя на повороте при бортовых фрикционах в два раза меньше, чем при простом дифе-ренциале. Это снижение нагрузки достигается за счет снижения потери в тормозе, а также вследствие понижения средней скорости машины на повороте. Зависимость между коэ-фициентами нагрузки двигателя и параметром поворота показана на диаграмме фиг.
 

Регуляторы являются приборами, предназначенными для того, чтобы удерживать в возможно близких друг к другу пределах изменения средней скорости машины, вызванные изменениями движущих сил или сил сопротивлений.
 

Если бы движение машины было равномерно, если бы она шла всегда одинаково быстро, то оценка 40 км в час полностью характеризовала бы ее скорость — одну и ту же в любой момент движения. Но машина движется неравномерно; за час скорость ее много раз резко меняется, и когда нам говорят, что машина прошла в час 40 км, то это дает нам представление лишь о некоторой средней скорости машины за этот час и ничего не говорит о скорости ее в тот или другой определенный момент, в том или другом определенном месте ее пути. Час — это слишком большой промежуток времени, за который скорость движения машины может меняться много раз.
 

Средняя скорость машины при выполнении арифметики тем самым приблизительно равна 10000 операций в секунду. При выполнении логических программ быстродействие резко возрастает. В минимальном комплекте в состав процессора входит оперативная память объемом 8192 байта. Правда, объем памяти при необходимости может быть расширен до 64 Кбайт.
 

На маршруте ABCDE длиной 147 км Турист может сам выбирать способ передвижения. На обратном пути из пункта Е в пункт А он поступил по-другому: до пункта D дошел пешком, преодолев расстояние в 24 км, в пункте D пересел на лошадь и добрался до пункта В за 3 ч 20 мин, а от пункта Л до пункта А доехал на машине за 1 ч 12 мин. Определите скорость передвижения туриста на машине и на лошади, если средние скорости машины и лошади были постоянными при движении от А к S и обратно.
 

Как найти скорость, формула

Все задачи, в которых присутствует движение объектов, их перемещение или вращение, так или иначе связаны со скоростью.

Данный термин характеризует перемещение объекта в пространстве за определенный отрезок времени – число единиц расстояния за единицу времени. Он является частым «гостем» как разделов математики, так и физики.

Исходное тело может менять свое расположение как равномерно, так и с ускорением. В первом случае величина скорости статична и в ходе движения не меняется, во втором наоборот – увеличивается или уменьшается.

1

Как найти скорость – равномерное движение

Если скорость движения тела оставалась неизменной от начала перемещения и до окончания пути, то речь идет о перемещении с постоянным ускорением – равномерном движении. Оно может быть прямолинейным или же криволинейным. В первом случае траекторией перемещения тела является прямая.

Тогда V=S/t, где:

• V – искомая скорость,
• S – пройденное расстояние (общий путь),
• t – общее время движения.

2

Как найти скорость – ускорение постоянно

Если объект двигался с ускорением, то его скорость по мере движения менялась. В таком случае найти искомую величину поможет выражение:

V=V (нач) + at, где:

• V (нач) – первоначальная скорость движения объекта,
• a – ускорение тела,
• t – общее время пути.

3

Как найти скорость – неравномерное движение

В данном случае имеет место ситуация, когда разные участки пути тело проходило за разное время.
S(1) – за t(1),

S(2) – за t(2) и т.д.

На первом участке движение происходило в “темпе” V(1), на втором – V(2) и т.д.

Чтобы узнать скорость перемещения объекта на всем пути (ее среднее значение) воспользуйтесь выражением:

V= (S(1)+S(2))/(t(1)+t(2)).

В случае вращения речь идет об угловой скорости, определяющей угол, на который поворачивается элемент за единицу времени. Обозначается искомая величина символом ω (рад/с).

Δφ – пройденный угол (приращение угла),
Δt – прошедшее время (время движения – приращение времени).

В случае, если вращение равномерное, искомая величина (ω) связана с таким понятием как период вращения – за какое время наш объект совершит 1 полный оборот. В таком случае:

• ω = 2π/T, где:
  π – константа ≈3,14,
• T – период.
• Или ω = 2πn, где:
  π – константа ≈3,14,
• n – частота обращения.

При известной линейной скорости объекта для каждой точки на пути движения и радиусе окружности, по которой она перемещается, для нахождения скорости ω потребуется следующее выражение:

1. ω = V/R, где:
   V – численное значение векторной величины (линейной скорости),
2. R – радиус траектории следования тела.

5

Как найти скорость – сближение и отдаление точек

• В подобного рода задачах уместным будет использование терминов скорость сближения и скорость отдаления.
• Если объекты направляются друг к другу, то скорость сближения (отдаления) будет следующей:
  V (сближ) = V(1) + V(2), где V(1) и V(2) – скорости соответствующих объектов.
• Если одно из тел догоняет другое, то V (сближ) = V(1) – V(2), V(1) больше V(2).

6

Как найти скорость – движение по водоему

Если события разворачиваются на воде, то к собственной скорости объекта (движение тела относительно воды) добавляется еще и скорость течения (т.е. движение воды относительно неподвижного берега). Как взаимосвязаны эти понятия?

В случае перемещения по течению V=V(собст) + V(теч).
Если против течения – V=V(собств) – V(теч.).

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​\( g \)​, единицы измерения – м/с2.

Важно! \( g \) = 9,8 м/с2, но при решении задач считается, что \( g \) = 10 м/с2

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

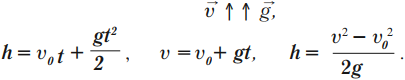
Если тело падает вниз без начальной скорости, то ​\( v_0 \)​ = 0.
Время падения рассчитывается по формуле:

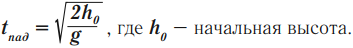
Тело брошено вверх:

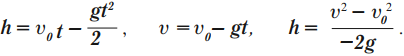
Если брошенное вверх тело достигло максимальной высоты, то ​\( v \)​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​\( v_0=v_{0x} \)​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​\( g \)​ и без начальной скорости ​\( v_{0y}=0 \)​.

Уравнение скорости:

Уравнение координаты:

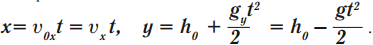
Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

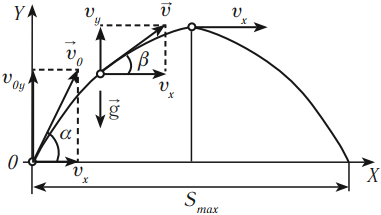
Уравнение скорости:

Уравнение координаты:

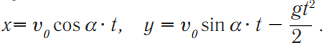
Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е. тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т

е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​\( v_0 \)​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​\( \alpha \)​, под которым тело брошено, будет равен углу, под которым оно упадет

тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​\( v_0 \)​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​\( \alpha \)​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Решение задач на среднюю скорость

Решение задач на среднюю скорость

Задачи простые, важно понять и запомнить формулу:

Если участков пути было два, тогда

Если три, то соответственно:

Как вы поняли, смысл таков: в знаменателе складываются отрезки времени, в

числители суммируем расстояния пройденные за соответствующие им отрезки

№1: Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 61

км/ч, а вторую половину времени – со скоростью 87 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения.

В задаче сказано о двух участках пути.

Среднюю скорость будем искать по формуле:

Пусть на весь путь автомобиль затратил t часов.

Значит за первую половину времени со скоростью 61 км/ч автомобиль прошёл

0,5∙t∙61 километров, а за вторую половину времени 0,5∙t∙87 километров, тогда:

№2: Половину времени, затраченного на дорогу, автомобиль ехал со скоростью 74

км/ч, а вторую половину времени – со скоростью 66 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

№3: Путешественник переплыл море на яхте со средней скоростью 17 км/ч.

Обратно он летел на спортивном самолете со скоростью 323 км/ч. Найдите

среднюю скорость путешественника на протяжении всего пути. Ответ дайте в

Мы не знаем, каким было расстояние, которое преодолел путешественник. Знаем

только, что это расстояние было одинаковым на пути туда и обратно.

Когда расстояние не указано его принимают за 1 (в данном случае — одно море).

Тогда время, которое путешественник плыл на яхте, равно 1/17, а время, затраченное

на полет, равно 1/323.

Общее время равно:

Тогда средняя скорость равна:

Путешественник переплыл море на яхте со средней скоростью 20 км/ч. Обратно он

летел на спортивном самолете со скоростью 480 км/ч. Найдите среднюю скорость

путешественника на протяжении всего пути. Ответ дайте в км/ч.

№5: Первую треть трассы автомобиль ехал со скоростью 90 км/ч, вторую треть –

со скоростью 60 км/ч, а последнюю – со скоростью 45 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения. В

задаче сказано о трёх участках пути.

Среднюю скорость будем искать по формуле:

Обозначим весь пусть S.

Тогда первую треть пути автомобиль ехал:

Вторую треть пути автомобиль ехал:

Последнюю треть пути автомобиль ехал:

№6: Первую треть трассы автомобиль ехал со скоростью 60 км/ч, вторую треть –

со скоростью 120 км/ч, а последнюю – со скоростью 110 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

№7: Первый час автомобиль ехал со скоростью 100 км/ч, следующие два часа – со

скоростью 90 км/ч, а затем два часа – со скоростью 80 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения. В

задаче сказано о трёх участках пути.

Среднюю скорость будем искать по формуле:

Исходя из условия мы можем определить протяжённость каждого участка:

Первый участок пути составил 1∙100 = 100 километров.

Второй участок пути составил 2∙90 = 180 километров.

Третий участок пути составил 2∙80 = 160 километров.

№8: Первые два часа автомобиль ехал со скоростью 50 км/ч, следующий час – со

скоростью 100 км/ч, а затем два часа – со скоростью 75 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

№9: Первые 120 км автомобиль ехал со скоростью 60 км/ч, следующие 120 км — со

скоростью 80 км/ч, а затем 150 км — со скоростью 100 км/ч. Найдите среднюю

скорость автомобиля на протяжении всего пути. Ответ дайте в км/ч.

Чтобы найти среднюю скорость нужно весь путь разделить на всё время движения. В

задаче сказано о трёх участках пути.

Среднюю скорость будем искать по формуле:

Протяжённость участков дана. Определим время, которое затратил автомобиль на

каждый участок: на первый участок автомобиль затратил 120/60 часов, на второй

участок 120/80 часов, на третий 150/100 часов.

Находим среднюю скорость:

№10: Первые 190 км автомобиль ехал со скоростью 50 км/ч, следующие 180 км — со

скоростью 90 км/ч, а затем 170 км — со скоростью 100 км/ч. Найдите среднюю

Курс повышения квалификации

Сейчас обучается 807 человек из 76 регионов

Курс профессиональной переподготовки

Сейчас обучается 358 человек из 68 регионов

Курс повышения квалификации

Современные педтехнологии в деятельности учителя

• Курс добавлен 23.09.2021
• Сейчас обучается 46 человек из 23 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-309466

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Расстояние и скорость

Положение каждой физической точки можно описать с помощью координатных осей. Другими словами, системой, которая по отношению к исследуемому телу остаётся неизменной. Изменение положения относительно другого объекта можно представить пройденным расстоянием. Фактически это путь, для которого известно начало и конец. С физической точки зрения, расстояние — величина, являющаяся размерностью длины, и выражающаяся в её единицах.

В математике мера пройденного пути тесно связана с метрическим пространством, то есть положением, где существует пара (x, d), определённая в декартовом произведении. Соответственно, если координату принять за x, y, можно сказать следующее:

• начало пути и его конец обозначают точками с координатами d (x, y) и p (x, y);
• пройденное расстояние можно определить, отняв из конечных координат начальные;
• изменение положения будет нулевым, когда d = p.

В физике расстояние измеряют единицами длины. В соответствии с СИ за размерность берут метр. Расстояние — мера пройденного пути, то есть длина. Если необходимо просто определить изменение положения без учёта, когда и как оно произошло, используют координатные оси. Но при нахождении пройденного пути за время в формуле для расстояния должна учитываться ещё одна величина — скорость.

Обозначают эту характеристику символом V. Характеризует она быстроту перемещения в выбранной системе отсчёта. По определению скорость равняется производной радиус-вектора точки по времени. Иными словами, это значение, задающееся положением в пространстве относительно неизменной координаты, за которую чаще всего принимается начало.

Но на самом деле не всё так однозначно. Скорость необязательно должна быть одинаковой на всём пути. На определённых промежутках она может увеличиваться или уменьшаться, поэтому в математике под её значением понимают среднюю величину. Считается, что тело движется равномерно при прохождении установленного расстояния.

Постоянная скорость

Описание формулы.

Самый простой случай в физике — равномерное движение. Скорость постоянна, не меняется на протяжении всего пути. Есть даже скоростные константы, сведенные в таблицы, — неизменные величины. К примеру, звук распространяется в воздухе со скоростью 340,3 м/с.

А свет — абсолютный чемпион в этом плане, он обладает самой большой в нашей Вселенной скоростью — 300 000 км/с. Эти величины не меняются от начальной точки движения до конечной. Они зависят только от среды, в которой движутся (воздух, вакуум, вода и пр.).

Равномерное движение часто встречается нам и в повседневной жизни. Так работает конвейер на заводе или фабрике, фуникулер на горных трассах, лифт (за исключением очень коротких периодов пуска и остановки).

График такого движения очень прост и представляет собой прямую линию. 1 секунда — 1 м, 2 секунды — 2 м, 100 секунд — 100 м. Все точки находятся на одной прямой.

Использование онлайн-калькулятора

В интернете существуют сервисы, позволяющие находить параметр даже тем, кто не знает формулы или слабо ориентируется в теме. С их помощью можно решать довольно сложные задания, которые требуют скрупулёзного расчёта и немалой затраты времени. Онлайн-вычисление обычно занимает не более нескольких секунд, а за достоверность результата можно не беспокоиться.

Воспользоваться сайтами-калькуляторами сможет любой пользователь, имеющий подключение к интернету и установленный веб-браузер с поддержкой Flash-технологии. Никакой регистрации или указания личных данных сервисы, предлагающие такого рода услуги, не требуют. Система автоматически рассчитает ответ.

Из множества сайтов можно выделить три наиболее популярных среди потребителей:

1. Справочный портал «Калькулятор».
2. Allcalc.
3. Fxyz.

Расчёт скорости любого тела несложен. Главное, знать формулы и правильно определить вид перемещения. При этом всегда можно воспользоваться услугами онлайн-калькуляторов. Через них решить поставленную задачу или проверить свои расчёты.

Перемещение материальной точки

Пусть материальная точка совершает движение по оси X все время в одном направлении. Тогда перемещением этой материальной точки за отрезок времени $\Delta t=t_2-t_1$ будет отрезок $\Delta x=x_2-x_1$. Если материальная точка все время своего движения перемещалась в одном направлении, то пройденный путь ($\Delta s$) равен по модулю величине перемещения:

Если точка движется сначала в одном направлении, затем останавливается и движется в противоположном направлении, (например, так движется тело брошенное вертикально вверх) то путь равен сумме модулей перемещений в обоих направлениях:

Закон сложения

Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.

Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.

Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.