Как найти скорость зная среднюю скорость

Как вы рассчитываете среднюю скорость и расстояние?

Вы можете узнать среднюю скорость объекта, если знаете пройденное расстояние и время, которое на это потребовалось. Формула скорости: скорость = расстояние ÷ время.

Как найти среднюю скорость, зная только скорость? Сложите две скорости вместе.

Тогда, разделить сумму на два. Это даст вам среднюю скорость за всю поездку. Итак, если Бен ехал со скоростью 40 миль в час в течение 2 часов, а затем со скоростью 60 миль в час в течение еще 2 часов, его средняя скорость составляет 50 миль в час.

Почему средняя скорость отличается от средней скорости четырех отрезков ходьбы?

Средняя скорость объекта ничего не говорит нам о том, что происходит с ним между начальной и конечной точками. Средняя скорость отличается от средней скорости тем, что учитывает направление движения и общее изменение положения.

Средняя скорость и средняя скорость одинаковы? Люди могут подумать, что средняя скорость и средняя скорость — это просто разные названия одной и той же величины, но средняя скорость зависит от расстояния а средняя скорость зависит от смещения. Если объект меняет направление в своем путешествии, то средняя скорость будет больше, чем модуль средней скорости.

Могут ли средняя скорость и средняя скорость быть одинаковыми?

Люди могут подумать, что средняя скорость и средняя скорость — это просто разные названия одной и той же величины, но средняя скорость зависит от расстояния а средняя скорость зависит от смещения. Если объект меняет направление в своем путешествии, то средняя скорость будет больше, чем модуль средней скорости.

Могут ли средняя скорость и средняя скорость быть равны? Если объект движется прямолинейно и в том же направлении, то величина перемещение равно общей длине пути. В этом случае величина средней скорости равна средней скорости.

Обязательно ли, чтобы средняя скорость и средняя скорость были равны?

Нет, средняя скорость не всегда равна модулю вектора средней скорости. Средняя скорость — это пройденное расстояние, деленное на интервал времени, тогда как вектор средней скорости — это вектор смещения, деленный на интервал времени.

Как найти среднюю скорость без расстояния и времени? Только что прибавьте начальную скорость к конечной скорости и разделите сумму на два. Результат — средняя скорость.

Скорость тела. Средняя скорость тела

      Решение задач на движение опирается на хорошо известную из курса физики формулу

позволяющую найти путь   S ,   пройденный за время   t   телом, движущимся с постоянной скоростью   v .

      Сразу же сделаем важное

      Замечание 1. Единицы измерения величин   S ,   t   и   v   должны быть согласованными. Например, если путь измеряется в километрах, а время – в часах, то скорость должна измеряться в км/час.

      В случае, когда тело движется с разными скоростями на разных участках пути, вводят понятие средней скорости, которая вычисляется по формуле

(1)

      Например, если тело в течение времени   t₁   двигалось со скоростью   v₁ ,  в течение времени   t₂   двигалось со скоростью   v₂ ,  в течение времени   t₃   двигалось со скоростью   v₃ ,  то средняя скорость

(2)

      Задача 1. По расписанию междугородный автобус должен проходить путь в   100   километров с одной и той же скоростью и без остановок. Однако, пройдя половину пути, автобус был вынужден остановиться на   25   минут. Для того, чтобы вовремя прибыть в конечный пункт, водитель автобуса во второй половине маршрута увеличил скорость на   20   км/час. Какова скорость автобуса по расписанию?

      Решение. Обозначим буквой   v   скорость автобуса по расписанию и будем считать, что скорость   v   измеряется в км/час. Изобразим данные, приведенные в условии задачи 1, на рисунке 1.

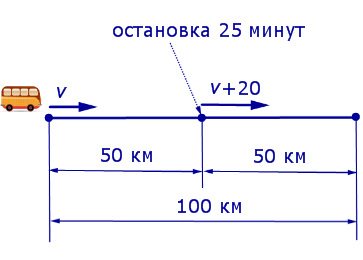
Рис. 1

      Тогда

      – время движения автобуса по расписанию (в часах);

      – время, за которое автобус проехал первую половину пути (в часах);

      v + 20   – скорость автобуса во второй половине пути (в км/час);

      – время, за которое автобус проехал вторую половину пути (в часах).

      В условии задачи дано время остановки автобуса –   25   минут. Его необходимо выразить в часах, чтобы все единицы измерения были согласованными:

      Теперь можно составить уравнение, исходя из того, что автобус прибыл в конечный пункт вовремя, а, значит, время, которое он был в пути, плюс время остановки должно равняться времени движения автобуса по расписанию:

      Решим это уравнение:

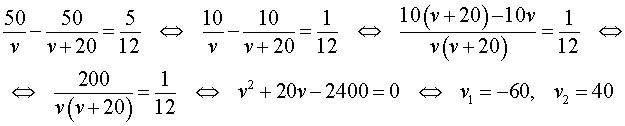
      По смыслу задачи первый корень должен быть отброшен.

      Ответ.   40   км/час.

      Задача 2. (МИОО) Первый час автомобиль ехал со скоростью   120   км/час, следующие три часа – со скоростью   105   км/час, а затем три часа – со скоростью   65   км/час. Найдите среднюю скорость автомобиля на протяжении всего пути.

      Решение. Воспользовавшись , получаем

      Ответ.   90   км/час.

      Задача 3. Первую половину пути поезд шел со скоростью   40   км/час, а вторую половину пути – со скоростью   60   км/час. Найдите среднюю скорость поезда на протяжении всего пути.

      Решение. Обозначим буквой   S   длину всего пути, выраженную в километрах. Изобразим данные, приведенные в условии задачи 3, на рисунке 2.

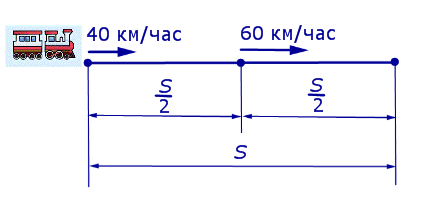
Рис. 2

      Тогда

      – время, за которое поезд прошел первую половину пути, выраженное в часах;

      – время, за которое поезд прошел вторую половину пути, выраженное в часах.

      Следовательно, время, за которое поезд прошел весь путь, равно

      В соответствии с средняя скорость поезда на протяжении всего пути

      Ответ.   48   км/час.

      Замечание 2. Средняя скорость поезда в задаче 3 равна   48   км/час, а не   50   км/час, как иногда ошибочно полагают, вычисляя чисел (скоростей)   40   км/час и   60   км/час. Средняя скорость не равна среднему арифметическому скоростей, а является величиной, вычисляемой по .

Средняя скорость

Как можно сравнивать скорости неравномерных движений?

Один из способов решения этой задачи — использование в физике такого понятия, как средняя скорость.

Идея состоит в том, чтобы пренебречь изменением скорости во время рассматриваемого промежутка времени, а рассматривать только начальный и конечный момент. Такое измерение удобно, если нам необходимо оценить общий результат движения.

В самом деле, как правило, целью движения является прибытие в конечный пункт к необходимому моменту времени

Как именно это достигнуто, зачастую неважно. Тело могло начать движение сразу и равномерно достигнуть конечного пункта

Могло, как автомобиль, сперва разогнаться, а потом затормозить в конечном пункте к тому же моменту времени. Наконец, тело могло двигаться «рывками», делая ряд остановок во время перемещения, но прибыть в конечный пункт, опять же, к тому же моменту времени.

Во всех трех приведенных случаях важно то, что тело начало и закончило движение в одни и те же моменты и переместилось за время движения на одно и то же расстояние. Что происходило во время движения, не рассматривается

Скорость, рассчитываемая только по начальному и конечному моменту движения, называется средней. Для нахождения средней скорости необходимо найти отношение общего перемещения материальной точки ко времени, за которое это перемещение произошло.

$$v_{ср}={\Delta x_{общ} \over \Delta t_{общ}}$$

Например, если автомобиль начал разгон в нулевой момент времени с нулевой скорости, разогнался до 50 км/ч, потом притормозил до 40 км/ч, и потом, через минуту, остановился в 600 м от начального пункта, то для нахождения средней скорости его движения необходимо 600 м поделить на 60 с. Средняя скорость составит 10 м/с.

Рис. 3. Средняя скорость.

Что мы узнали?

Одним из способов оценки скорости неравномерного движения является средняя скорость. При расчете средней скорости исходят только из начального и конечного моментов движения. А изменениями скорости между этими моментами пренебрегают. Средняя скорость удобна, если необходимо оценить общий результат движения, не обращая внимания на мелкие детали.

1. /10

   Вопрос 1 из 10

Как найти среднюю скорость на том же расстоянии?

Формула средней скорости

1. Средняя скорость = общее пройденное расстояние / общее затраченное время.
2. Когда расстояние постоянно: Средняя скорость = 2xy/x+y; Где x и y — две скорости, с которыми было пройдено одно и то же расстояние.

Являются ли средняя скорость и средняя скорость одинаковыми, если не объяснить почему?

Ответ: Средняя скорость и средняя скорость не всегда совпадают средняя скорость связана с перемещением тела тогда как средняя скорость связана с расстоянием, пройденным телом. Средняя скорость определяется делением полного перемещения тела на время.

Почему мы можем рассчитать только среднюю скорость? Поскольку средняя скорость равна общему пройденному расстоянию, деленному на общее пройденное время. Если вы проезжаете одинаковое расстояние с каждой скоростью, вы проводите больше времени на более низкой скорости, поэтому более низкая скорость «учитывается больше» при вычислении среднего значения.

Средняя скорость и средняя скорость одинаковы? Люди могут подумать, что средняя скорость и средняя скорость — это просто разные названия одной и той же величины, но средняя скорость зависит от расстояния а средняя скорость зависит от смещения. Если объект меняет направление в своем путешествии, то средняя скорость будет больше, чем модуль средней скорости.

Перемещение и мгновенная скорость

Запись модуля вектора υ примет вид:

υ=υ=υx2+υy2+υz2=x2+y2+z2.

Чтобы перейти от декартовых прямоугольных координат к криволинейным, применяют правила дифференцирования сложных функций. Если радиус-вектор r является функцией криволинейных координат r=rq1, q2, q3, тогда значение скорости запишется как:

υ=drdt=∑i=13∂r∂qi∂qi∂r=∑i=13∂r∂qiq˙i.

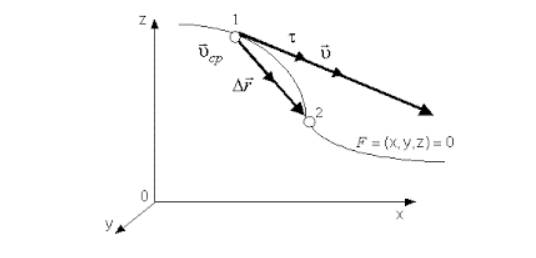
Рисунок 3. Перемещение и мгновенная скорость в системах криволинейных координат

При сферических координатах предположим, что q1=r; q2=φ; q3=θ, то получим υ, представленную в такой форме:

υ=υrer+υφeφ+υθφθ, где υr=r˙; υφ=rφ˙sin θ; υθ=rθ˙; r˙=drdt; φ˙=dφdt; θ˙=dθdt; υ=r1+φ2sin2θ+θ2.

Определение 4

Мгновенной скоростью называют значение производной от функции перемещения по времени в заданный момент, связанной с элементарным перемещением соотношением dr=υ(t)dt

Пример 1

Дан закон прямолинейного движения точки x(t)=,15t2-2t+8. Определить ее мгновенную скорость через 10 секунд после начала движения.

Решение

Мгновенной скоростью принято называть первую производную радиус-вектора по времени. Тогда ее запись примет вид:

υ(t)=x˙(t)=.3t-2; υ(10)=.3×10-2=1 мс.

Ответ: 1 мс.

Пример 2

Движение материальной точки задается уравнением x=4t-,05t2. Вычислить момент времени tост, когда точка прекратит движение, и ее среднюю путевую скорость υ.

Решение

Вычислим уравнение мгновенной скорости, подставим числовые выражения:

υ(t)=x˙(t)=4-,1t.

4-,1t=;tост=40 с;υ=υ()=4;υ=∆υ∆t=-440-=,1 мс.

Ответ: заданная точка остановится по прошествии 40 секунд; значение средней скорости равняется ,1 мс.

Всё ещё сложно?
Наши эксперты помогут разобраться

Все услуги

Решение задач

от 1 дня / от 150 р.

Курсовая работа

от 5 дней / от 1800 р.

Реферат

от 1 дня / от 700 р.

Частные случаи нахождения средней скорости

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила: м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Сергей Валерьевич

Главная&nbsp>&nbsp Wiki-учебник&nbsp>&nbsp Физика&nbsp>&nbsp7 класс&nbsp>

Суть и определение

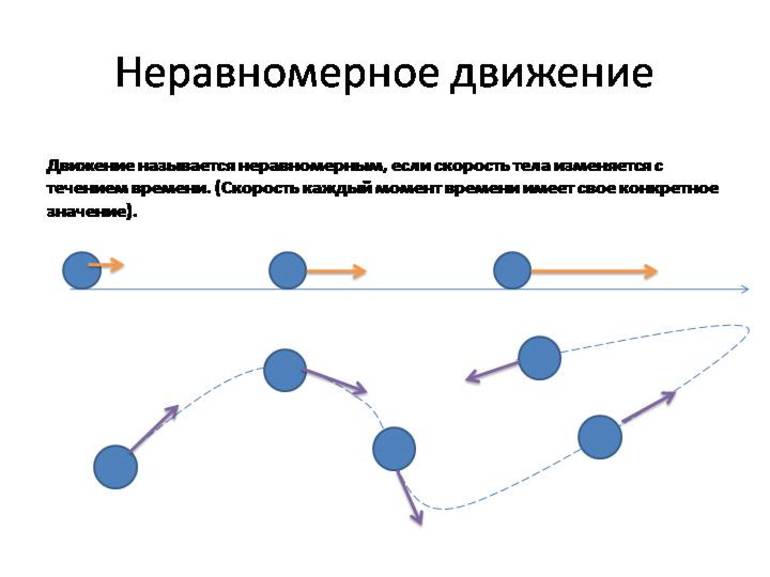
Суть неравномерного движения изучают в седьмом классе средней школы на уроках физики. В школьном учебнике приводится определение, что неравномерным считается такое изменение материальной точки в пространстве, при котором меняется скорость. При этом отмечается, что она может изменяться и по направлению.

Исходя из этого, можно сделать заключение, что движение, сопровождающее изменением скорости или траектории, является неравномерным. Например, вращение шара по окружности, выстрел из лука. При этом перемещение может быть равноускоренным, то есть состоять из чередования различных неравномерных движений. Как пример можно привести переключение скоростей в передвигающемся автомобиле.

Средняя скорость — это относительный параметр. Определяется он отношением пройденного пути к затраченному для этого времени. Предполагать, что для его нахождения можно просто сложить известные мгновенные скорости и разделить результат на их количество, в корне неверно. Под мгновенной характеристикой понимается скорость, существующая в определённой точке на данный момент.

Например, спидометр, установленный в машине, регистрирует ежесекундно именно мгновенную скорость. Поэтому для нахождения среднего показателя используется следующая формула: V = s / t, где:

В качестве единицы измерения используется отношение метров на секунды в соответствии с Международной системой измерений (СИ). Следует отметить, что когда траектория пути не является прямолинейной, то пройденное материальной точкой расстояние будет больше, чем её перемещение. Для описания такого случая вводится понятие средней путевой скорости, являющейся скалярной величиной. При этом её значение будет отличаться от средней скорости перемещения.

Случается так, что движение точки через один и тот же промежуток времени изменяется на одинаковую величину. В этом случае движение называют равнопеременным. Оно может быть как равнозамедленным, так и равноускоренным. Ускорение или замедление не зависит от изменения скорости за единицу времени. Но, зная поведение тела и его начальную скорость, можно вычислить, с какой скоростью оно будет двигаться в любой промежуток времени. Для этого используют выражение: v = v0 + a * Δt.

Как рассчитать среднюю скорость?

Средняя скорость рассчитывается по формуле разделение вашего смещения (вектор, указывающий от вашего начального положения до вашего конечного положения) на общее время; средняя скорость рассчитывается путем деления общего пройденного расстояния на общее время.

Каковы 3 способа расчета среднего? 4.2.

Выделяют три основных типа среднего: среднее, медиана и мода. Каждый из этих методов работает немного по-разному и часто приводит к немного отличающимся типичным значениям. Среднее значение является наиболее часто используемым средним значением. Чтобы получить среднее значение, вы складываете все значения и делите эту сумму на количество значений.

Как найти среднемесячное значение?

Разделите текущую сумму на общее количество дней в месяц, который прошел до сих пор. Затем умножьте на общее количество дней в месяце.

Как решить проблемы со средней скоростью? Как рассчитать среднюю скорость

1. Чтобы получить среднюю скорость, с, разделите общее расстояние на затраченное время: Dt.D t.
2. Чтобы получить затраченное время t, разделите общее расстояние на скорость: Ds. Дс.
3. Чтобы получить расстояние D, умножьте скорость на количество времени: s × t.

Аналог средней температуры в механике

В каких случаях каверзно сформулированные условия задачи подталкивают нас к поспешному необдуманному ответу? Если говорится о «частях» пути, но не указывается их протяжённость, это настораживает даже мало искушённого в решении подобных примеров человека. А вот если в задаче прямо указывается на равные промежутки, например, «первую половину пути поезд следовал со скоростью…», или «первую треть пути пешеход прошагал соскоростью…», и далее подробно расписывается, как объёкт передвигался на оставшихся равных участках, то есть известно соотношение S 1 = S 2 = … = S n и точные значения скоростей v 1, v 2, … v n, наше мышление нередко даёт непростительную осечку. Считается среднее арифметическое скоростей, то есть все известные значения v складываются и делятся на n. В итоге ответ получается неверный.

Скорость. Время. Расстояние

Скорость

Вы наблюдали, что вокруг нас постоянно что-то или кто-то движется. Некоторые объекты – быстро, а некоторые – совсем медленно. Например, по лесной тропе прогуливается человек, по шоссе едет автомобиль, по воздуху летит вертолет. Все они движутся. Но автомобиль движется быстрее, чем человек, а вертолет – быстрее автомобиля.

В математике, величиной характеризующей быстроту движения объектов называют скоростью.

Скорость движения – это расстояние, пройденное за единицу времени. Единицей времени может быть:  1 секунда, 1 минута, 1 час.

Давайте вместе разберем две простые задачи.

Легковая машина прошла 120 км за 2 часа. В течение каждого часа она проходила одинаковое расстояние. Сколько км прошла машина за 1 час?

120 : 2 = 60 (км) – пройдет машина за 1 час.

Таким образом, скорость движения машины 60 км в час. Сокращенно запишем так:

60 км/ч.

Космический корабль пролетает 8 000 м за 1 секунду. Как по-другому записать его скорость?

Его скорость можно записать так: 8 000 м/с. Мы знаем, что 1 км = 1000 м, поэтому скорость корабля можно записать по-другому: 8 км/с.

Посмотрите скорость движения некоторых  животных

Какое животное самое медленное, самое быстрое? Обратите внимание, что скорость можно записать по-разному: в зависимости от того, сколько сантиметров, метров, километров кто-то пролетает, проползает или пробегает за секунду, минуту, час

Время

С единицами времени вы уже знакомы. Это: секунда, минута, час, сутки, неделя, месяц, год, век.

Расстояние

Расстояние – это длина дороги, соединяющая начало и конец пути.

Расстояние измеряется в следующих единицах:

Миллиметр

Сантиметр

Дециметр

Метр

Километр

Оптимальная скорость для автомобиля — второй фактор выбора режима поездки

Главным критерием выбора скоростного режима являются далеко не возможности машины, а ваши соображения о безопасности и уверенности поездки. Если вы считаете, что ехать со скоростью 90 км/ч при данных условиях опасно, то лучше выбрать более комфортный и уверенный режим. Тем не менее, существуют определенные рекомендации от производителей.

Первое, о чем стоит вспомнить в таком контексте разговора, является средний расход. Если вы будете поддерживать скорость машины на уровне 90 километров в час, то расход будет максимально близким к паспортным показателям расхода на трассе. Многие водители переживают по поводу того, что их машина на трассе расходует больше топлива, чем указано в документах. Происходит это по таким причинам:

• на обгоне автомобиль вынужден потреблять в разы больше топлива в силу необходимости быстрого разгона;
• постоянное торможение и трогание с места в пробке или на различных преградах также дает плюс к расходу;
• движение на скорости свыше 100 километров в час начинает значительно увеличивать расход бензина;
• производитель рассчитывает трассовые режимы поездки на среднюю скорость 90 километров в час;
• под данный показатель происходит настройка всех функций и узлов автомобиля, передаточных чисел и двигателя.

Именно по этим причинам средние показатели расхода часто оказываются на порядок больше паспортных замеров. При определении расхода в трассовом режиме для технических характеристик машины производитель выполняет тестирование транспорта не треке, где машина едет с постоянной одной рекомендованной скоростью. Именно это позволяет достичь столь занимательных цифр расхода топлива.

Для получения максимальных выгод в расходе топлива и прочих характеристиках вашего автомобиля экспериментируйте и пробуйте разные режимы поездки. Не лишни будет и почитать отзывы о том, как люди эксплуатируют ваш тип транспорта. Это поможет максимально упростить эксплуатацию машины, сделать меньшим расход топлива и предсказать любые особенности поведения транспортного средства. Помните, что скорость должна быть оправданной. Предлагаем подборку видео ДТП, случившихся в частности из-за высокой скорости:

Формула скорости математика 4 класс

С какой скоростью черепах ползла после камня, если она проползла 33 см?

3. Поезд шёл до станции 7 ч со скоростью 63 км/ч, а после станции поезд проехал ещё 4 ч. С какой скоростью поезд проедет путь от станции, если всего он прошёл 741 км?

Составные задачи на расстояние.

Образец:

Травоядный динозавр сначала бежал 3 ч со скоростью 6 км/ч, а потом он бежал ещё 4 ч со скоростью 5 км/ч. Какое расстояние пробежал травоядный динозавр?

Рассуждаем так. Это задача в одном направлении.

Составим таблицу.

Слова « скорость », «время», «расстояние» запишем зеленой ручкой.

Скорость (V) Время (t) Расстояние (S)

С. — 6 км/ч Зч? км

П. — 5 км/ч 4ч?км? км

Составим план решения этой задачи. Чтобы узнать какое расстояние пробежал динозавр, надо знать, какое расстояние он пробежал, потом и какое расстояние он пробежал сначала.

S Sп Sс

Чтобы найти расстояние, надо скорость умножить на время.

Sс =Vс t с

6· 3 = 18 (км) — расстояние, которое про­бежал динозавр сначала. Чтобы найти расстояние, надо скорость умножить на время.

Sп = Vп tп

5 4 = 20 (км) — расстояние, которое про­бежал динозавр потом.

18 + 20 = 38 (км)

Составим выражение:6 3 + 5 4 = 38(км)

Ответ: 38 км пробежал травоядный динозавр.

Реши задачу.

1. Ракета сначала летела 28 с со скоростью 15 км/с, а оставшийся путь летела 53 с со скоростью 16 км/с. Какое расстояние проле­тела ракета?

2. Утка сначала плыла 3 ч со, скоростью 19 км/ч, а потом она плыла ещё 2 ч со скоро­стью 17 км/ч. Какое расстояние проплыла утка?

3. Кит полосатик сначала плыл 2 ч со скорос­тью 22 км/ч, а потом он плыл ещё 2 ч со ско­ростью 43 км/ч. Какое расстояние проплыл кит полосатик?

4. Теплоход до пристани шёл 3 ч со скоростью 28 км/ч, а после пристани плыл ещё 2 ч со скоростью 32 км/ч. Какое расстояние про­плыл теплоход?

Задачи на нахождение времени совместной работы.

Образец:

Привезли 240 саженцев елей. Первый лесник может посадить эти ели за 4 дня, а второй за 12 дней. За сколько дней оба лесника могут выполнить задание, рабо­тая вместе?

240: 4 = 60 (саж,) за 1 день сажает пер­вый лесник.

240: 12 — 20 (саж.) за 1 день сажает вто­рой лесник.

60 + 20 = 80 (саж.) за 1 день сажают оба лесника. 240:80 = 3(дн.)

Ответ: за 3 дня лесники посадят сажен­цы, работая вместе.

Реши задачу.

1. В мастерской 140 мониторов. Один мастер отремонтирует их за 70 дней, а другой, за 28 дней. За сколько дней оба мастера отре­монтируют эти мониторы, если будут рабо­тать вместе?

2. Было 600 кг горючего. Один трактор израсходовал его за 6 дней, а другой – за 3 дня. За сколько дней тракторы израсходуют это горючее, работая вместе?

3. Надо перевезти 150 пассажиров. Один катер перевезёт их за 15 рейсов, а другой за 10 рейсов. За сколько рейсов эти катера перевезу всех пассажиров, работая вместе?

4. Один ученик может сделать 120 снежинок 60 мин, а другой — за 30 мин. Сколько потребуется времени ученикам, если они будут работать вместе?

5. Один мастер может изготовить 90 шайбочек за 30 мин, другой—‘за 15 мин. За какое вре­мя они изготовят 90 шайбочек при совмест­ной работе?

⇐ Предыдущая234567891011

Частные случаи нахождения средней скорости

1. Два одинаковых участка пути. Пусть первую половину пути тело двигалось со скоростью , а вторую половину пути — со скоростью . Требуется найти среднюю скорость движения тела.

• Пусть — общая длина пройденного пути. Тогда на первом участке пути тело двигалось в течение интервала времени . Аналогично, на втором участке пути тело двигалось в течение интервала времени .
• Тогда средняя скорость движения равна:

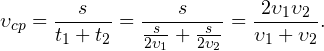
2. Два одинаковых интервала движения. Пусть тело двигалось со скоростью в течение некоторого промежутка времени, а затем стало двигаться со скоростью в течение такого же промежутка времени. Требуется найти среднюю скорость движения тела.

• Пусть — общее время пути. Тогда путь, пройденный телом в течение первой половины времени движения, равен: . Аналогично, путь, пройденный телом в течение второй половины времени движения, равен: .
• Тогда средняя скорость движения равна:

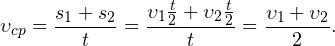
Здесь мы получили единственный случай, когда средняя скорость движения совпала со средним арифметическим скоростей и на двух участках пути.

Решим напоследок задачу из Всероссийской олимпиады школьников по физике, прошедшей в прошлом году, которая связана с темой нашего сегодняшнего занятия.

Тело двигалось с, и средняя скорость движения составила 4 м/с. Известно, что за последние с движения средняя скорость этого же тела составила 10 м/с. Определите среднюю скорость тела за первые с движения.

Пройденный телом путь составляет: м. Можно найти также путь, который прошло тело за последние с своего движения: м. Тогда за первые с своего движения тело преодолело путь в м. Следовательно, средняя скорость на этом участке пути составила: м/с.

Задачи на нахождение средней скорости движения очень любят предлагать на ЕГЭ и ОГЭ по физике, вступительных экзаменах, а также олимпиадах. Научиться решать эти задачи должен каждый школьник, если он планирует продолжить свое обучение в вузе. Помочь справиться с этой задачей может знающий товарищ, школьный учитель или репетитор по математике и физике. Удачи вам в изучении физики!

Находим среднюю скорость и средний расход поездки по факту

Если замеры средней скорости поездки важны для вас в коммерческих целях или в качестве отчетности для фирмы, в которой вы работаете, то проще всего купить GPS-навигатор, который обладает функцией учета скорости и времени, проведенного в дороге. Этот прибор полностью заменит бортовой компьютер и сможет без применения различных формул показать вам среднюю скорость поездки.

В иных случаях можно пользоваться более грубыми методами определения. Для замеров вам потребуется секундомер, который будет определять рабочее время поездки. То есть, для нас важна каждая секунда, которую автомобиль проводит в дороге. Время, проведенное на заправках или в придорожных кафе зачастую в расчет не входит. Задачи для точного замера следующие:

• перед поездкой сбросьте суточный счетчик километров на нуль, начните новый отчет пробега;
• установите на приборной панели автомобиля секундомер и не забывайте включать его каждый раз, когда трогаетесь;
• как только вы остановились не по причине дорожной обстановки, а по собственному желанию, выключайте секундомер;
• после прибытия в пункт назначения выпишите данные суточного счетчика с точностью до одного километра;
• также выпишите данные секундомера с точностью до минуты — это даст вам возможность развязать уравнение;
• подставьте полученные данные в формулу Vсредняя = S / t, где V — это средняя скорость, S — пройденное расстояние, а t — затраченное на поездку время.

Предположим, на поездку у вас ушло ровно 5 часов, а пройденное по спидометру расстояние оказалось 300 километров. Это значит, что средняя скорость вашего автомобиля во время движения составила 60 км/ч. Если вы будете практиковать определение средней скорости для каждой дальней поездки, то будете удивлены низкими показателями.

Часто создается впечатление, что средняя скорость должна быть около 120 километров в час, но на деле оказывается меньше 60. Подобным образом вы сможете просчитать средний расход топлива. Нужно затраченные литры поделить на сотни километров пройденного расстояния. К примеру, если вы проехали 300 километров, то делать сумму литров нужно на 3.

Мгновенная и средняя скорость

Скорость движения материальной точки — это физическая величина, характеризующая быстроту движения и равная отношению пройденной длины ко времени, за которое эта длина была пройдена:

$$v={Δl \over Δt}$$

Поскольку длина в системе СИ измеряется в метрах, а время — в секундах, то скорость измеряется в метрах в секунду.

Рис. 1. Скорость движения в физике

Наиболее точной является мгновенная скорость, то есть такая скорость, при которой величина $Δt$ стремится к нулю. При этом получающееся значение скорости $v$ может быть постоянным, а может меняться в каждой точке пройденного пути.

Вычисление мгновенной скорости позволяет моделировать движение материальной точки наиболее детально. Однако в реальных условиях настолько большая точность чаще всего не требуется

Как правило, важно, чтобы движение было совершено к определённому моменту времени, а как именно это произошло — не имеет значения

В этом случае используется понятие средней скорости. Средняя скорость отличается от мгновенной тем, что для вычисления используется сразу весь отрезок времени. Величина $Δt$ в приведённой формуле равна общему времени движения:

$$v_{ср}={l_{общ} \over t_{общ}}$$

Математическое обнаружение скрытой ошибки

В решаемом нами примере пройденный телом (поездом или пешеходом) путь будет равен произведению nS_n (так как мы n раз складываем равные участки пути, в приведённых примерах — половинки, n = 2, или трети, n = 3). О полном же времени движения нам ничего не известно. Как определить среднюю скорость, если знаменатель дроби (3) явно не задан? Воспользуемся соотношением (2), для каждого участка пути определим t_n = S_{n :} v_n. Сумму рассчитанных таким образом промежутков времени запишем под чертой дроби (3). Ясно, что, для того чтобы избавиться от знаков «+», нужно приводить все S_{n :} v_n к общему знаменателю. В результате получается «двухэтажная дробь». Далее пользуемся правилом: знаменатель знаменателя идёт в числитель. В итоге, для задачи с поездом после сокращения на S_n имеем v_ср = nv₁v_{2 :} v₁ + v₂, n = 2 (4)_. Для случая с пешеходом вопрос -, как найти среднюю скорость, решается ещё сложнее: v_ср = nv₁v₂v_{3 :} v_1v2 + v₂v₃ + v₃v₁, n = 3(5).

Как же рассчитать скорость

• через формулу нахождения мощности;
• через дифференциальные исчисления;
• по угловым параметрам и так далее.

В этой статье рассматривается самый простой способ с самой простой формулой — нахождение значения этого параметра через расстояние и время. Кстати, в формулах дифференциального расчета также присутствуют эти показатели. Формула выглядит следующим образом:

• v — скорость объекта,
• S — расстояние, которое пройдено или должно быть пройдено объектом,
• t — время, за которое пройдено или должно быть пройдено расстояние.

Как видите, в формуле первого класса средней школы нет ничего сложного. Подставив соответствующие значения вместо буквенных обозначений, можно рассчитать быстроту передвижения объекта. Например, найдем значение скорости передвижения автомобиля, если он проехал 100 км за 1 час 30 минут. Сначала требуется перевести 1 час 30 минут в часы, так как в большинстве случаев единицей измерения рассматриваемого параметра считается километр в час (км/ч). Итак, 1 час 30 минут равно 1,5 часа, потому что 30 минут есть половина или 1/2 или 0,5 часа. Сложив вместе 1 час и 0,5 часа получим 1,5 часа.

Теперь нужно подставить имеющиеся значения вместо буквенных символов:

v=100 км/1,5 ч=66,66 км/ч

Здесь v=66,66 км/ч, и это значение очень приблизительное (незнающим людям об этом лучше прочитать в специальной литературе), S=100 км, t=1,5 ч.

Таким нехитрым способом можно найти скорость через время и расстояние.

А что делать, если нужно найти среднее значение? В принципе, вычисления, показанные выше, и дают в итоге результат среднего значение искомого нами параметра. Однако можно вывести и более точное значение, если известно, что на некоторых участках по сравнению с другими скорость объекта была непостоянной. Тогда пользуются таким видом формулы:

vср=(v1+v2+v3+…+vn)/n, где v1, v2, v3, vn — значения скоростей объекта на отдельных участках пути S, n — количество этих участков, vср — средняя скорость объекта на всем протяжении всего пути.

Эту же формулу можно записать иначе, используя путь и время, за которое объект прошел этот путь:

• vср=(S1+S2+…+Sn)/t, где vср — средняя скорость объекта на всем протяжении пути,
• S1, S2, Sn — отдельные неравномерные участки всего пути,
• t — общее время, за которое объект прошел все участки.

Можно записать использовать и такой вид вычислений:

• vср=S/(t1+t2+…+tn), где S — общее пройденное расстояние,
• t1, t2, tn — время прохождения отдельных участков расстояния S.

Но можно записать эту же формулу и в более точном варианте:

vср=S1/t1+S2/t2+…+Sn/tn, где S1/t1, S2/t2, Sn/tn — формулы вычисления скорости на каждом отдельном участке всего пути S.

Таким образом, очень легко найти искомый параметр, используя данные выше формулы. Они очень просты, и как уже было указано, используются в начальных классах. Более сложные формулы базируются на этих же формулах и на тех же принципах построения и вычисления, но имеют другой, более сложный вид, больше переменных и разных коэффициентов. Это нужно для получения наиболее точного значения показателей.

Задача №4

Автомобиль проехал равномерно участок дороги длиной $3.5 \space км$ за $3 \space мин$. Нарушил ли правила дорожного движения водитель, если на обочине расположен дорожный знак “скорость не более $50 \frac{км}{ч}$”?

Дано:$S = 3.5 \space км$$t = 3 \space мин$

$\upsilon — ?$

Показать решение и ответ

Скрыть

Решение:

После того, как мы рассчитаем скорость движения автомобиля, нам нужно будет сравнить ее со скоростным ограничением в $50 \frac{км}{ч}$. Для того чтобы это сделать, нужно, чтобы скорость тоже была выражена в километрах в час.

Так как водитель двигался равномерно, рассчитывать скорость его движения мы будем по формуле:$\upsilon = \frac{S}{t}$.

Путь $S$ у нас и так выражен в километрах, а время — в минутах. Поэтому, перед рассветом скорости переведем время из минут в часы:$t = 3 \space мин = \frac{3}{60} \cdot ч = 0.05 \space ч$.

Теперь мы можем рассчитать скорость движения автомобиля:$\upsilon = \frac{3.5 \space км}{0.05 \space ч} = 70 \frac{км}{ч}$.

Получается, что водитель нарушил правила дорожного движения, ведь $70 \frac{км}{ч} > 50 \frac{км}{ч}$.

Ответ: нарушил.