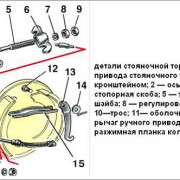
Передаточное число коробки передач: что нужно знать

1.6 Определение общего передаточного отношения и передаточного отношения ременной передачи

Принимаем редуктор конически-цилиндрический с

_ред

Следовательно передаточное отношение ременной передачи вычисляется:

_{общдввых}

_ред

_{рпобщред}

1.7 Определение скоростей, мощностей и моментов на валах

Определение угловых скоростей

Определение мощностей

Определение крутящих моментов

Определение угловых скоростей

Табл.6 Силовые и кинематические параметры привода

Номер вала	n, мин-1	ω, с-1	P, кВт	T, Нм
1	1410	147,58	3000	2,033
2	440,6	46,12	2850	61,8
3	110	11,53	2654	57,54
4	22	2,3	2468,1	1073

1.8 Выбор редуктора

Принимаем редуктор КЦ1 200. Параметры редуктора из табл. 19 и 27

Таблица 4. Габаритные и присоединительные размеры двух ступенчатых конически-циллиндрических редукторов типа КЦ250

Тип	аω1	аω2	В	А	А1	L	L1	L2	L3	l	l1	l2	l3	Н
КЦ 1-200	200	300	375	250	900	480	310	255	460	435
Н1	Н2	Н3	n	d
225	180	—	4	17

Т_таблК_р≥

_таблр

1270·0,8>57,54

Т.о. условие выполняется

Таблица 5. Характеристика зацепления цилиндрических двухступенчатых горизонтальных редукторов типа КЦ250

Номинальное передаточное число	Вращающий момент на выходном валу, Н*м	Радиальная сила на валу, Н	КПД
входном	выходном
20	1270	2500	8750	0,98

Схема ременной передачи:1-ведущий шкив,2-ведомый шкив,3-ремень

Исходные данные (полученные из кинематического расчёта привода): Мощность на ведущем валу:  P1 = 3 кВт; Частота вращения ведущего вала:  n1 = 1410 об/мин.; Передаточное число ремённой передачи:  U = 3,2. 1)   Рассчитываем крутящий момент на ведущем валу, затем выбираем по таблице сечение ремня и диаметр меньшего шкива:  Принимаем: d1=100 мм; Сечение ремня S = 81 мм2, типа А. (ГОСТ 1284.1-80) 2)   Определяем диаметр большого шкива: 3) Уточняем передаточное число с учётом относительного скольжения: ε≈ 0.01: Определяем расхождение от заданного U: (∆i / i) · 100% = ((|iст – i|) / iст) · 100% = ((|3,2-3.23|) / 3,2) · 100% = 0,9%

4) Проводим сравнение  ; — условие выполняется. 5) Определяем ориентировочное значение межосевого расстояния: ; т.к. i=3,2, то с=1;  a’=320 мм. 6) Определяем ориентировочное значение длины ремня: мм Из стандартного ряда длину ремня L принимаем: L=1320 мм. 7) Уточняем межосевое расстояние:  ; а=325 мм. 8) Определяем скорость ремня: м/с.9) Определяем число пробегов ремня в секунду: 5,6  с-1 10) Определяем угол обхвата ремней малого шкива: м/с. 11) Проводим проверку ;  158,9ᵒ≥120ᵒ— условие выполняется. 12) Определяем окружную силу на шкивах: Н.

13) Определяем ориентировочное значение числа устанавливаемых ремней: м/с. где — допустимое полезное напряжение; А1 – площадь поперечного сечения ремня; k0– полезное напряжение ремня, МПа; м/с. где V – скорость ремня, м/с; ν – частота пробегов ремня; bh – ширина ремня по нейтральному слою;ku – коэффициент влияния передаточного числа; ca – коэффициент, учитывающий влияние угла обхвата на тяговую способность; cp – коэффициент режима работы. 14) Определяем силы, действующие на валы:  где А1 = 81 мм2, z =2, k0 = 3,49МПа; =180-158,9=21,1- угол между ветвями ремня. =1115,3Н.

StudFiles.ru

Виды приводных ремней

Видов ремней достаточно много, так как используются они в разных условиях. Где-то нужно передать очень большую мощность так, чтобы ремень не порвался и не растянулся. Где-то ремень не должен проскальзывать. Где-то ремень должен крутиться очень-очень быстро и мало изнашиваться со временем. А где-то нужно передать вращение на большое расстояние и под углом.

Очень распространенная классификация ремней – по поперечному сечению или форме. Основные виды: 1 — плоские ремни, 2 – клиновые ремни, 3 – ремни круглого сечения (пассики), 4 – многоручьевые ремни (или поликлиновые), 5 – зубчатые ремни.

Рис. 12. Виды приводных ремней

В крупной промышленной технике самые распространенные ремни – клиновые и поликлиновые. Они достаточно толстые по сечению и имеют увеличенную за счет боковой поверхности площадь сцепления со шкивами.

В небольших электронных устройствах чаще используются плоские ремни и пассики (ремни с круглым сечением).

Рис. 13. Четыре прядильные машины приводятся в движение от плоских приводных ремней с линейного вала. Лейпциг , Германия, около 1925 года

Плоские ремни широко использовались в 19-м и начале 20 века на фабриках для передачи движения на несколько машин с одного линейного вала (англ. line shaft). Они широко применялись и применяются в лесопильных станках, молотилках, электрогенераторах.

В станках с ЧПУ (3D-принтерах, плоттерах, лазерных станках) используются зубчатые ремни, так-так они сохраняют постоянное передаточное отношение и не проскальзывают.

Обзор передач

На сегодняшний день существуют такие виды механических передач:

• Зубчатые.
• Ременные.
• Фрикционные.
• Червячные.
• Цепные.
• Храповые.
• Волновые.

В целом же, механические передачи разделяются по таким критериям:

• В зависимости от передачи движения от ведущего звена к ведомому: передачи трением и передачи зацеплением.
• В зависимости от соотношения скоростей ведомого и ведущего звеньев: замедляющие передачи (они же редукторы), ускоряющие передачи (мультипликаторы).
• В зависимости от расположения осей валов: передачи с перекрещивающимися, пересекающимися и параллельными осями.

Стоит указать, что замедляющие передачи на практике применяются гораздо чаще, нежели ускоряющие. Этот факт объясняется тем, что скорости вращения двигателей зачастую гораздо выше требуемой скорости вала исполнительного механизма или машины.

Расчет оборотов двигателя по передаточному числу

Как рассчитать передаточное отношение шестерен механической передачи.

В этой статье я приведу пример расчета передаточного отншения шестерен разного диаметра, с разным количеством зубьев

Данный расчет применяется в том случае, когда важно определить к примеру скорость вращения вала редуктора при известной скорости привода и характеристиках зубьев

Естественно, можно произвести замеры частоты вращения выходного вала, однако в некоторых случаях требуется именно расчет. Помимо этого, в теоретической механике, при конструировании различных узлов и механизмов требуется рассчитать шестерни, чтобы получить заданную скорость вращения.

Термин передаточное число является весьма неоднозначным. Он перекликается с термином передаточное отношение, что не совсем верно. Говоря о передаточном числе, мы подразумеваем сколько оборотов совершит ведомое колесо (шестерня) относительно ведущего.

Для правильного понимания процессов и строения шестерни – следует предварительно ознакомится с ГОСТ 16530-83.

Итак, рассмотрим пример расчета с использованием двух шестерен.

Чтобы рассчитать передаточное отношение мы должны иметь как минимум две шестерни. Это называется зубчатая передача. Обычно первая шестерня является ведущей и находится на валу привода, вторая шестерня называется ведомой и вращается входя в зацепление с ведущей. Пи этом между ними может находится множество других шестерен, которые называются промежуточными. Для упрощения расчета рассмотрим зубчатую передачу с двумя шестернями.

В примере мы имеем две шестерни: ведущую (1) и ведомую (2). Самый простой способ заключается в подсчете количества зубьев на шестернях. Посчитаем количество зубьев на ведущей шестерне. Так же можно посмотреть маркировку на корпусе шестерни.

Представим, что ведущая шестерня (красная) имеет 40 зубьев, а ведомая(синяя) имеет 60 зубьев.

Разделим количество зубьев ведомой шестерни на количество зубьев ведущей шестерни, чтобы вычислить передаточное отношение. В нашем примере: 60/40 = 1,5. Вы также можете записать ответ в виде 3/2 или 1,5:1.

Такое передаточное отношение означает, что красная, ведущая шестерня должна совершить полтора оборота, чтобы синяя, ведомая шестерня совершила один оборот.

Теперь усложним задачу, используя большее количество шестерен. Добавим в нашу зубчатую передачу еще одну шестерню с 14 зубьями. Сделаем ее ведущей.

Начнем с желтой, ведущей шестерни и будем двигаться в направлении ведомой шестерни. Для каждой пары шестерен рассчитываем свое передаточное отношение. У нас две пары: желтая-красная; красная-синяя. В каждой паре рассматриваем первую шестерню как ведущую, а вторую как ведомую.

В нашем примере передаточные числа для промежуточной шестерни: 40/14 = 2,9 и 60/40 = 1,5.

Умножаем значения передаточных отношений каждой пары и получаем общее передаточное отношение зубчатой передачи: (20/7) × (30/20) = 4,3. То есть для вычисления передаточного отношения всей зубчатой передачи необходимо перемножить значения передаточных отношений для промежуточных шестерен.

Определим теперь частоту вращения.

Используя передаточное отношение и зная частоту вращения желтой шестерни, можно запросто вычислить частоту вращения ведомой шестерни. Как правило, частота вращения измеряется в оборотах в минуту (об/мин) Рассмотрим пример зубчатой передачи с тремя шестернями. Предположим, что частота вращения желтой шестерни 340 оборотов в минуту. Вычислим частоту вращения красной шестерни.

Будем использовать формулу: S1 × T1 = S2 × T2,

S1 – частота вращения желтой (ведущей) шестерни,

Т1 – количество зубьев желтой (ведущей) шестерни;

S2- частота вращения красной шестерни,

Т2 – количество зубьев красной шестерни.

В нашем случае нужно найти S2, но по этой формуле вы можете найти любую переменную.

340 rpm × 7 = S2 × 40

Получается, если ведущая, желтая шестерня вращается с частотой 340 об/мин, тогда ведомая, красная шестерня будет вращаться со скоростью примерно 60 об/мин. Таким же образом рассчитываем частоту вращения пары красная-синяя. Полученный результат – частота вращения синей шестерни – будет являться искомой частотой вращения всей зубчатой передачи.

Источник

Формула расчета параметров прямозубой передачи

Чтобы определить параметры прямозубой шестеренки, потребуется выполнить некоторые предварительные вычисления. Длина начальной окружности равна π×D, где D — ее диаметр.

Расчет модуля зубчатого колеса

Шаг зацепления t – это расстояние между смежными зубами, измеренное по начальной окружности. Если это расстояние умножить на число зубов z, то мы должны получить ее длину:

проведя преобразование, получим:

Если разделить шаг на число пи, мы получим коэффициент, постоянный для данной детали зубчатой передачи. Он и называется модулем зацепления m.

размерность модуля шестерни — миллиметры. Если подставить его в предыдущее выражение, то получится:

выполнив преобразование, находим:

Отсюда вытекает физический смысл модуля зацепления: он представляет собой длину дуги начальной окружности, соответствующей одному зубцу колеса. Диаметр окружности выступов De получается равным

где h’- высота головки.

Высоту головки приравнивают к m:

Проведя математические преобразования с подстановкой, получим:

Диаметр окружности впадин Di соответствует De за вычетом двух высот основания зубца:

где h“- высота ножки зубца.

Для колес цилиндрического типа h“ приравнивают к значению в 1,25m:

Устройство зубчатого колеса

Выполнив подстановку в правой части равенства, имеем:

что соответствует формуле:

и если выполнить подстановку, то получим:

Иначе говоря, головка и ножка зубца относятся друг к другу по высоте как 1:1,25.

Следующий важный размер, толщину зубца s принимают приблизительно равной:

• для отлитых зубцов: 1,53m:
• для выполненных путем фрезерования-1,57m, или 0,5×t

Поскольку шаг t приравнивается к суммарной толщине зубца s и впадины sв, получаем формулы для ширины впадины

• для отлитых зубцов: sв=πm-1,53m=1,61m:
• для выполненных путем фрезерования- sв= πm-1,57m = 1,57m

Характеристики конструкции оставшейся части зубчатой детали определяются следующими факторами:

• усилия, прикладываемые к детали при эксплуатации;
• конфигурация деталей, взаимодействующих с ней.

Детальные методики исчисления этих параметров приводятся в таких ВУЗовских курсах, как «Детали машин» и других. Модуль шестерни широко используется и в них как один из основных параметров.

Для отображения шестеренок методами инженерной графики используются упрощенные формулы. В инженерных справочниках и государственных стандартов можно найти значения характеристик, рассчитанные для типовых размеров зубчатых колес.

Планетарный редуктор и планетарная передача — теория

Рассмотрен принцип действия планетарной передачи, указаны преимущества и недостатки применения планетарных редукторов. Приведена схема планетарной передачи и расчет передаточного отношения редуктора.

Планетарный редуктор и планетарная передача

Зубчатая передача

Зубчатая передача

Устройство планетарного механизма основано на вращении тел зубчатой передачи, которые непосредственно взаимодействуют с главным двигателем. Именно такое соединение и служит для передачи силы от редуктора до других механизмов с изменением скорости их вращения. Таким образом происходит передача крутящего момента от двигателя на колеса через основную ось, главную шестерню и сателлиты.
Вообще устройство зубчатой передачи достаточно простое и понятное. Вот, что входит в конструкцию обычной передачи.
Для соединения с главной передачей имеются две зубчатые шестерни, таким образом происходит зацепление. При движении происходит передача скорости вращения с главной шестерни на ведомую за счет зацепов. Наименьшее колесо в конструкции называется шестерней, а наибольшее будет главным и ведомым колесом.

Планетарный механизм

Схема планетарной передачи

Редукторы с зубчатой передачей, колеса которых имеют движущиеся оси, называются планетарными. Внутри расположены зубчатые колеса, перемещающиеся на своих, геометрических осях. Такие шестерни получили название сателлиты, потому что вся конструкция очень похожа на солнечную систему. Главные шестерни называются центральными колесами. Сателлиты крепятся на своих осях и вращаются вокруг главной передачи при помощи водила, которое движется так же, как и центральное колесо, вокруг главной оси. Центральное колесо остается неподвижным, а другие шестерни можно заблокировать или разблокировать полностью.

Если центральное колесо неподвижно, то второе постоянно движется. Ведущим здесь является вал подвижного колеса, а ведомым-водила. Если разблокировать все зубчатые колеса вместе с ведомым, то такая передача будет дифференциальной. Выделяют два основных и ведущих звена и одно ведомое.

При подробном рассмотрении простейшей планетарной передачи мы видим: ведущее колесо или водило, ведомое с тремя сателлитами, вращающимися вокруг центральной оси и центральное, неподвижное колесо.

Передаточное отношение

Чтобы рассчитать передаточное отношение редуктора, необходимо заметить определенное количество неподвижных звеньев(1,2,3 и Н) и условно задать им поступательное вращение со скоростью wH, равное скорости вращения водила, но с обратным знаком. Скорость зацепления зубчатых колес не изменяется. Таким образом скорость + wH +(- wH)=0, то есть водило будет остановлено. Если водило неподвижно, тогда планетарная передача превращается в зубчатую, где все колеса неподвижны. Сателлиты не учитываются. Их вращение будет положительным при одинаковом вращении шестерен, а отрицательным при противоположном вращении:i=(? 1 -? H)/(? 3 -? H)=-(z 3 /z 1), где z 1 и z. Если колесо 3 закреплено неподвижно, то угловая скорость водила Н = 1 /[1+(z 3 /z 1)], а передаточное отношение i =1+z 3 /z 1.

Как обычно, для работы редуктора с одноступенчатой передачей при больших нагрузках становится мало, поэтому стали изготавливать двух и трех ступенчатые редукторы, а иногда и четырех ступенчатые. Чаще всего применяется двухступенчатая передача.

Двухступенчатая планетарная передача.

Схема двухступенчатой планетарной передачи

Для других редукторов передаточное отношение высчитывается таким же способом. Для двухступенчатого редуктора, где центральное колесо 1—ведущее, водило Н2 — ведомое, центральные колеса 3 и 4 закреплены в корпусе, передаточное отношение i=1+z 2 z 3 /z 1 z 4.

При всех достоинствах планетарного редуктора, нужно знать, что при сильном вращении шестерни, КПД всего механизма сильно ухудшается.

Нагрузка от центрального колёса водила восприниматься всеми шестеренками (1-6) одинаково, при этом их размеры значительно меньше, чем у обычной передачи. Следовательно, главными преимуществами планетарной передачи являются большая скорость вращения, небольшой вес и компактность. Дифференциальные передачи используются в автомобиле для разложения движения, а так же в различных станках. К минусам такой передачи относится ее трудоемкое изготовление и сложная сборка на предприятии. Такие редукторы благодаря своим преимуществам находят свое применение во многих отраслях производства: в машиностроении, приборах, станкостроении, в транспорте.

Использован материал из книги «Детали машин» Гузенков П.Г.

Так же по теме предлагаем статью «Планетарный редуктор» с примером расчета передаточного отношения и анимированными схемами ступеней планетарного редуктора.

Изменение передаточного отношения КПП: тюнинг коробки передач

Как известно, наилучшие динамические показатели достигаются в диапазоне оборотов максимального крутящего момента, а не мощности. Фактически, при нижнем и верхнем значении частоты вращения коленчатого вала крутящий момент двигателя меньше максимального.

Получается, чем больше обороты будут отличаться  от оборотов максимального крутящего момента, тем медленнее разгоняется автомобиль. В стандартных КПП передаточное отношение каждой ступени подобрано так, чтобы водителю было комфортно разгонять машину на низких передачах, после чего на повышенных можно поддерживать набранную скорость одновременно с экономией топлива.

Если же отбросить экономичность, тогда путем ряда доработок коробки можно улучшить динамику. Прежде всего, сужается диапазона частот, которые мотор развивает при езде на одной передаче. Фактически, передачи делаются более короткими, а также сближаются передаточные отношения передач, которые расположены рядом (сближенный ряд КПП).

На практике, мотор в этом случае быстро выходит на максимальные обороты на более низкой передаче, однако после переключения на ступень выше обороты не падают, например, 3500 об/мин. на 1800, а остаются на отметке около 2500. Фактически, после переключения «вверх» обороты все равно остаются в диапазоне максимального крутящего момента.

Для решения такой задачи можно использовать колеса с меньшим радиусом, а также требуется установить другую главную пару редуктора с измененным передаточным числом (например, 3.9 или 4.1 вместо 3.7). Начнем с использования «стоковых» деталей.

Как правило, если модель автомобиля выпускается с разными двигателями (например, моторы 1.2, 1.4 и 1.6 литра), тогда главную пару для КПП в паре с 1.6 литровым двигателем используют от той версии, мотор которой менее мощный (в данном случае  двигатель 1.2 или 1.4).  

В результате  после установки главной пары 3.9 или 4.1 передаточное число на 5-й передаче будет почти таким же, как и на 4-й при главной паре 3.7. Также дополнительно понизит общее передаточное число трансмиссии использование  шин меньшего радиуса. В результате  динамика автомобиля станет лучше, однако будет потеряна экономичность 5-й передачи.

На высоких скоростях двигатель будет на 5-й раскручиваться до максимальных оборотов, что может доставлять дискомфорт водителю и пассажирам. По этой причине ряд передаточных чисел КПП нужно подбирать с учетом конкретных задач и целей, учитывая мощность мотора, вес автомобиля, а также предпочтения водителя.

Если делать более серьезные доработки, тогда можно собрать коробку передач с измененным набором шестерен.  Естественно, это дорого, однако удается сблизить ряды на всех передачах, а не только 4 и 5.

Кстати, подбором передаточных чисел трансмиссии можно или улучшить разгонную динамику, или же повысить экономичность. При этом на практике во втором случае изменения в устройство КПП вносятся достаточно редко, так как штатно передаточное отношение зачастую подобрано достаточно удачно.

Также добавим, что стандартную 5-и ступенчатую коробку иногда переделывают в 6-и ступенчатую (особенно в паре с тюнингованным форсированным двигателем). Фактически, в КПП интегрируется комплект шестой передачи

Важно понимать, что  помимо высокой стоимости такой доработки снижается общая надежность такой коробки

https://youtube.com/watch?v=S3XcGCWR-RI

Как рассчитать передаточное число

Необходимость определить передаточное число (коэффициент) КПП у водителей возникает редко. Основная причина — модернизация трансмиссии для получения лучших динамических характеристик. Коэффициенты передачи коробки передач разных ступеней закладывает конструктор при проектировании автомобиля. Их выбирают на основе мощностных параметров двигателя и целевого назначения транспортного средства. Для среднестатистического водителя закладывают передаточные отношения КПП главной и понижающих передач, обеспечивающие наибольшую экономичность. Те, кто хочет придать автомобилю большей динамики, рассчитывают характеристики самостоятельно.

Расчет без учета сопротивления

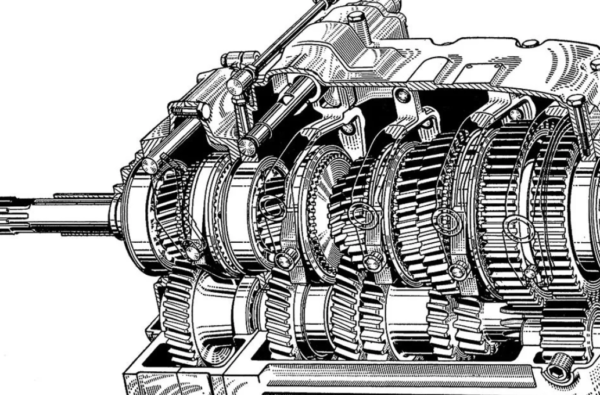
Узнать передаточный коэффициент можно в сопроводительной документации на агрегат (коробку или редуктор заднего моста). Когда документа нет, расчёт ведут самостоятельно. Для этого сравнивают количество оборотов на входном и выходном валах. Определение передаточного отношения главной пары редуктора заднего моста:

1. Вывесить приводное колесо, приподняв автомобиль домкратом.
2. На входном валу редуктора или на кардане поставить метку. Вторую отметку наносят на вывешенном колесе.
3. Вращая за ступицу считают обороты карданного вала. Когда колесо повернётся на 360°, оценивают положение второй отметки.
4. Определяют передаточный коэффициент, деля количество оборотов входного вала на 1 (поворот колеса). Полученное значение сравнивают со стандартными величинами.

К сведению!

Для более точного вычисления колесо поворачивают 10 раз.

В переднеприводных автомобилях главная пара размещается в КПП. Определение коэффициента выполняют по схожему принципу:

1. Снимают правое переднее колесо, открывая доступ к шкиву двигателя.
2. Ставят метки на ступице и хвостовике коленвала.
3. Включают 1 передачу и вращают шкив, считая обороты. Когда ступица провернётся на 360°, вычисляют передаточное отношение.
4. Процедуру выполняют для всех скоростей.

Для вычисления передаточного отношения главной передачи необходимо сравнить технические данные с полученными результатами. Для этого в интернете находят справочные таблицы, где указаны характеристики типовых КПП и выбирают совпадающую модель.

КПД зубчатой передачи

Более точный расчёт трансмиссии подразумевает вычисление крутящего момента с учётом всех сопротивлений. Передача вращения от двигателя к колёсам происходит с небольшими потерями на трение в зубчатых парах, подшипниках и уплотнениях. Эти помехи уменьшают выходной крутящий момент, а компенсируют его за счёт увеличения мощности двигателя. При расчёте используют КПД цилиндрической и конической зубчатой передачи. В первом случае он составляет 0,98, во втором — 0,97.

Общее определение

Наглядный пример изменения числа оборотов проще всего наблюдать на простом велосипеде. Человек медленно крутит педали. Колесо вращается значительно быстрее. Изменение количества оборотов происходит за счет 2 звездочек, соединенных в цепь. Когда большая, вращающаяся вместе с педалями, делает один оборот, маленькая, стоящая на задней ступице, прокручивается несколько раз.

Передачи с крутящим моментом

В механизмах используют несколько видов передач, изменяющих крутящий момент. Они имеют свои особенности, положительные качества и недостатки. Наиболее распространенные передачи:

Ременная передача самая простая в исполнении. Используется при создании самодельных станков, в станочном оборудование для изменения скорости вращения рабочего узла, в автомобилях.

Ремень натягивается между 2 шкивами и передает вращение от ведущего в ведомому. Производительность низкая, поскольку ремень скользит по гладкой поверхности. Благодаря этому, ременной узел является самым безопасным способом передавать вращение. При перегрузке происходит проскальзывание ремня, и остановка ведомого вала.

Передаваемое количество оборотов зависит от диаметра шкивов и коэффициента сцепления. Направление вращения не меняется.

На ремне имеются выступы, на шестерне зубчики. Такой тип ремня расположен под капотом автомобиля и связывает звездочки на осях коленвала и карбюратора. При перегрузе ремень рвется, так как это самая дешевая деталь узла.

Цепная состоит из звездочек и цепи с роликами. Передающееся число оборотов, усилие и направление вращения не меняются. Цепные передачи широко применяются в транспортных механизмах, на конвейерах.

Характеристика зубчатой передачи

В зубчатой передаче ведущая и ведомая детали взаимодействуют непосредственно, за счет зацепления зубьев. Основное правило работы такого узла – модули должны быть одинаковыми. В противном случае механизм заклинит. Отсюда следует, что диаметры увеличиваются в прямой зависимости от количества зубьев. Одни значения можно в расчетах заменить другими.

Например, между осями или точками на эвольвенте по средней линии Размер модуля состоит из ширины зуба и промежутка между ними. Измерять модуль лучше в точке пересечения линии основания и оси зубца. Чем меньше радиус, тем сильнее искажается промежуток между зубьями по наружному диаметру, он увеличивается к вершине от номинального размера. Идеальные формы эвольвенты практически могут быть только на рейке. Теоретически на колесе с максимально бесконечным радиусом.

Деталь с меньшим количеством зубьев называют шестерней. Обычно она ведущая, передает крутящий момент от двигателя.

Зубчатое колесо имеет больший диаметр и в паре ведомое. Оно соединено с рабочим узлом. Например, передает вращение с необходимой скоростью на колеса автомобиля, шпиндель станка.

Обычно посредством зубчатой передачи уменьшается количество оборотов и увеличивается мощность. Если в паре деталь, имеющая больший диаметр, ведущая, на выходе шестерня имеет большее количество оборотов, вращается быстрее, но мощность механизма падает. Такие передачи называют понижающими.

Зачем нужна паразитка

При взаимодействии шестерни и колеса происходит изменение сразу нескольких величин:

• количества оборотов;
• мощности;
• направление вращения.

Только в планетарных узлах с нарезкой зубьев по внутреннему диаметру венца сохраняется направление вращения. При наружном зацеплении ставится две одинаковые шестерни подряд. Их взаимодействие не меняет ничего, кроме направления движения. В этом случае обе зубчатые детали называются шестернями, колеса нет. Вторая, промежуточная, получила название «паразитка», поскольку в вычислениях не участвует, меняет только знак.

Виды зубчатых соединений

Зубчатое зацепление может иметь различную форму зуба на деталях. Это зависит от исходной нагрузки и расположения осей сопрягаемых деталей. Различают виды зубчатых подвижных соединений:

Самое распространенное и простое в исполнении прямозубое зацепление. Наружная поверхность зуба цилиндрическая. Расположение осей шестерни и колеса параллельное. Зуб расположен под прямым углом к торцу детали.

Выбор — передаточное число

Выбор передаточных чисел основной и дополнительной коробок передач производится при тяговом расчете автомобиля.
 

Выбор передаточного числа зависит от требуемой скорости движения автомобиля и мощности двигателя. У легковых автомобилей передаточное число колеблется в пределах от 3 2: 1 до 6 2: 1, у грузовых автомобилей — от 5 2: 1 до 7 5: I, а иногда и выше.
 

При выборе передаточного числа следует избегать общих множителей между числом ходов червяка и числом зубьев червячного колеса. В этом случае с помощью цилиндрической фрезы получают более чистую боковую поверхность и более высокую точность в положении начальной окружности червячного колеса, а также более благоприятные условия для работы и меньшего износа червячной передачи.
 

Вопрос о выборе передаточного числа мультипликатора представляет собой отдельную задачу.
 

Некоторые рекомендации по выбору передаточных чисел помещены в табл. 6.4. Наибольшие значения передаточных чисел следует принимать лишь в крайних случаях, так как передачи с наибольшими значениями i имеют большие габариты.
 

Может быть несколько причин, вызывающих желательность выбора передаточного числа у нижнего предела допустимых значений. Например, если нагрузка от трения составляет небольшую часть от общей нагрузки, то зубчатая передача может быть сделана более простой и экономичной.
 

К этим значениям и следует стремиться путем выбора передаточного числа кинематической схемы соединения электромагнита с исполнительным устройством при заданной противодействующей характеристике последнего и заданных размерах полюсного наконечника.
 

Вторым шагом при предварительном выборе основных параметров электропривода является выбор передаточного числа / редуктора, связывающего основной вал проектируемого механизма с двигателем.
 

Приведенные оптимальные передаточные числа являются лишь отправными величинами при выборе рабочего передаточного числа. Последнее выбирается после производства ряда расчетов с различными передаточными числами и сопоставления результатов с учетом максимально допустимой скорости механизма и требуемой мощности двигателя.
 

Если для привода используется высокоскоростной двигатель, то возникает проблема выбора передаточного числа механизма, связывающего двигатель с исполнительным звеном.
 

Таким образом, отмечая возможность улучшения тягово-сцепных свойств и экономичности автомобилей выбором оптимального передаточного числа межосевого дифференциала, необходимо констатировать, что окончательно эту задачу можно решить после проведения широких экспериментальных исследований по оценке фактических режимов работы автомобилей в различных дорожных условиях и выявлению истинного статистического распределения динамических реакций на осях и крутящих моментов, подводимых к ним, в том числе и при отборе мощности.
 

Средние значения КПД отдельных передач приведены в табл. 5.4, а рекомендации по выбору передаточных чисел — в табл. 5.5. Так как передачи с большими передаточными числами имеют большие габариты, их следует применять лишь в крайних случаях.
 

Если в системе привода с неизменным потоком возбуждения оптимальное значение передаточного числа редуктора не зависело от полного пути перемещения, то в рассматриваемой — системе эта зависимость — явно имеет место. Следовательно, выбор оптимального передаточного числа редуктора следует производить с учетом гистограммы перемещений рассматриваемого механизма.
 

Кривые статической характеристики муфты типа свключено — выключено. а — момент в функции скорости. б — момент в функции сигнала управления.| Видоизмененная характеристика момент — сигнал управления ( с учетом гистерезиса муфты типа включено — выключено.| Кривые нелинейных статических Характеристик, типичные для некоторых муфт вихревых токов и фрикционно-дисковых муфт. а — момент в функции скорости. о — момент в функции сигнала управления.

Если действительный рабочий цикл совершается в растянутый период времени, то значительное количество тепла может быть удалено путем естественного охлаждения; но если рабочий цикл уплотнен в малый отрезок времени и включает высокие ускорения, то следует выбирать муфту увеличенного размера или прибегать к искусственному охлаждению. Способность муфты управлять заданной нагрузкой рассматривается в связи с выбором передаточного числа зубчатой передачи в § 14 — 7; здесь будет рассмотрена лишь энергия, рассеиваемая в муфте.
 

Передаточное отношение для лодочного мотора

При выборе лодочного мотора на лодку мы часто в характеристиках видим такой пункт как “передаточное” отношение. И значение у него, в зависимости от модели, даже у одного бренда меняется в ту или иную сторону, иногда значительно. Если вы не знакомы с теорией и не специалист сервис центра, то этот материал как раз для вас. В этой статье мы коротко, наглядно, с примерами покажем, что же такое передаточное отношение для лодочного мотора.

Для начала обратимся к теории. Передаточное число – это есть отношение числа зубцов на ведомой шестеренке к числу зубцов на ведущей. Т.о. если у ведомой шестерни 40 зубцов а у ведущей 20, то мы имеет передаточное отношение равное 2. БОльшее значение этого показателя означает более быстрый разгон, мотор набирает высокие обороты очень быстро.

Во время проектирования при выборе передаточного отношения для того или иного мотора учитывается масса условий. Это и объем двигателя, его мощность, тип гребного винта и его диаметр, количество лопастей и т.д. Возможно кто то заметит, а зачем что то мудрить, просто сделайте большое передаточное отношение и все, мотор ведь будет скоростным. Но в отличии от автомобилей, у лодочных моторов нет возможности менять передаточные числа путем переключения передач. Коробка передач у лодочного мотора имеет три положения: вперед, нейтраль, назад. Если выставить передаточного отношение слишком высоким, то лодка разгонится очень быстро, но когда обороты мотора достигнут своего максимума разгон прекратиться. Т.е. максимальная скорость будет ограничена. Представьте если бы вы все время на автомобиле ездили бы на первой передаче. Разгоняетесь быстро, но вот добираться до места назначения приходилось бы значительно дольше. Вот поэтому производители учитывают множество параметров и делают мотор максимально сбалансированным, чтобы разгонялся резво, но и максимальная скорость была достаточной.

Для наглядности сравним два лодочных мотора Yamaha 60FETOL с передаточным отношением 2,33 и Honda BF 60 LRTU c отношением 2,09. Оба мотора имеют мощность в 60 л.с. Мотор Ямаха, имея большее отношение, несколько более тяговит, максимальную скорость он наберет быстрее, но вот сама “максималка” будет больше у мотора Хонда с его меньшим передаточным отношением. Но это верно только при использовании на обоих моторах гребных винтов с одинаковым шагом. Если же мы поставим на нашу Ямаху винт с 13 шагом, а на Хонду с 12, то ситуация может кардинально измениться. В таком случае Хонда может вытянуть лодку на режим глиссирования если и не быстрее, то по крайней мере за такое же время как и Ямаха.

В качестве вывода. При выборе мотора и рассмотрения такого параметра как “передаточное отношение” обязательно нужно учитывать на какую лодку планируется установить мотор (тип, водоизмещение) и гребной винт. Но хотим вас успокоить, если вы не преследуете на воде каких либо специфических целей, будь то соревнования на скорость или т.п., то на этот параметр обращать особого внимания не стоит. Производитель мотора сам за вас уже подумал и побеспокоился. Если же в скоростных характеристиках что-то не будет устраивать, это всегда можно выправить при правильном подборе гребного винта.

Метки Mercury Suzuki