Ошибки вычислений

Введение

Постановка вопроса. Виды погрешностей

Процесс исследования исходного объекта методом математического моделирования и вычислительного эксперимента неизбежно носит приближенный характер, так как на каждом этапе вносятся погрешности. Построение математической модели связано с упрощением исходного явления, недостаточно точным заданием коэффициентов уравнения и других входных данных. По отношению к численному методу, реализующему данную математическую модель, указанные погрешности являются неустранимыми, поскольку они неизбежны в рамках данной модели.

При переходе от математической модели к численному методу возникают погрешности, называемые погрешностями метода. Они связаны с тем, что всякий численный метод воспроизводит исходную математическую модель приближенно. Наиболее типичными погрешностями метода являются погрешность дискретизации и погрешность округления. При построении численного метода в качестве аналога исходной математической задачи обычно рассматривается её дискретная модель. Разность решений дискретизированной задачи и исходной называется погрешностью дискретизации. Обычно дискретная модель зависит от некоторого параметра (или их множества) дискретизации, при стремлении которого к нулю должна стремиться к нулю и погрешность дискретизации. Дискретная модель представляет собой систему большого числа алгебраических уравнений. Для её решения используется тот или иной численный алгоритм. Входные данные этой системы, а именно коэффициенты и правые части, задаются в ЭВМ не точно, а с округлением. В процессе работы алгоритма погрешности округления обычно накапливаются, и в результате, решение, полученное на ЭВМ, будет отличаться от точного решения дискретизированной задачи. Результирующая погрешность называется погрешностью округления (вычислительной погрешностью). Величина этой погрешности определяется двумя факторами: точностью представления вещественных чисел в ЭВМ и чувствительностью данного алгоритма к погрешностям округления.

Итак, следует различать погрешности модели, дискретизации и округления. В вопросе преобладания какой-либо погрешности ответ неоднозначен. В общем случае нужно стремиться, чтобы все погрешности имели один и тот же порядок. Например, нецелесообразно пользоваться разностными схемами, имеющими точность 10−6, если коэффициенты исходных уравнений задаются с точностью 10−2.

Расчёт ошибок косвенных измерений

Пусть искомая
величина Апри выбранном
методе косвенных измерений рассчитывается
по формуле:

A
= f(x₁
,x₂
,x₃
,…,x_n
) (12)

где x₁,x₂,…,x_n
— величины, найденные в результате прямых
измерений, с учётом ошибок о которых
шла речь выше. Из-за этих ошибок величина
«А»
так же будет определяться с ошибками.

Пусть X₁,X₂,…,X_N
— значения f(x₁
,x₂
,x₃
,…,x_n), вычисленные
для разных серий измерений (x₁,x₂,…,x_n).

Таблица 1

Таблица коэффициентов
Стьюдента

Абсолютной ошибкой
косвенных измерений, по аналогии с
аб­солютной ошибкой прямых измерений,
называют разность между ис­тинным
значением «А» и её значениями,
полученными в результате измерений:

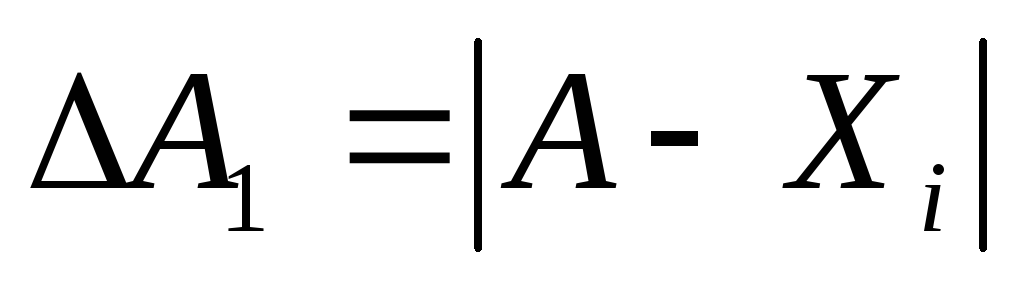(13)

Размерность
абсолютной ошибки совпадает с размерностью
определяемой величины. Относительной
ошибкой косвенных измерений называют
отвлечённое число:

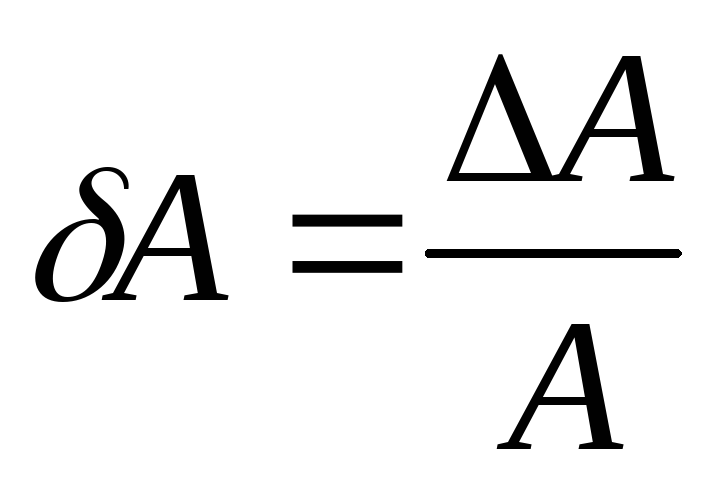(14)

Иногда относительную
ошибку выражают в процентах:

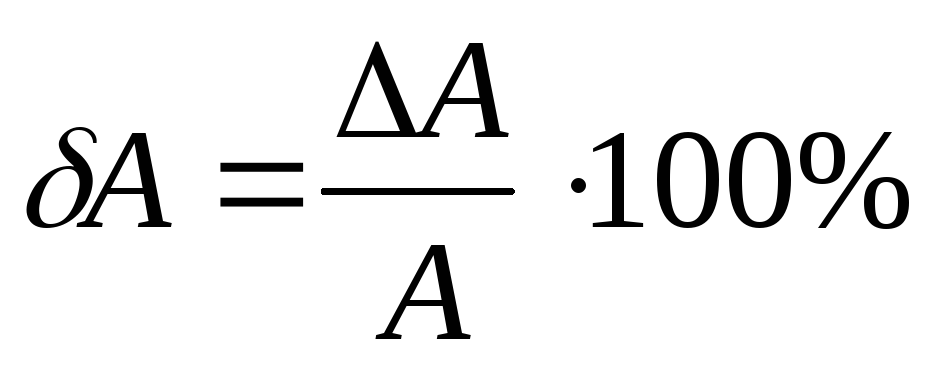(15)

Для определения
величины «А» в формулах (12)…(15) по
теории

вероятностей
следует брать величину Х, которую можно
определить двумя способами:

1) А
= Х
= (Х₁
+ Х₂
+…+Х_n)/n
(16)

2) A
= X
= f(x₁
+ x₂
+…+x_n)
(17)

где x₁,x₂
,…, x_n
определяют по формуле (3). Если ошибки
измерений малы, то оба способа дают
практически тождественные результаты.

Рассмотрим способы
нахождения ошибки величины А,
опреде­лённой из косвенных измерений,
по найденным значениям оши

бок прямых измерений.
Выше отмечалось, что возможны различные
соотношения между приборной систематической
и случайными ошибками.

1-й случай. Преобладают
приборные ошибки. В этом случае можно
дать только оценку максимальной ошибки.
Формулы для нахож­дения предельной
ошибки косвенных измерений по внешнему
виду совпадают с формулами дифференциального
исчисления. В связи с этим для предельной
абсолютной ошибки используется формула:

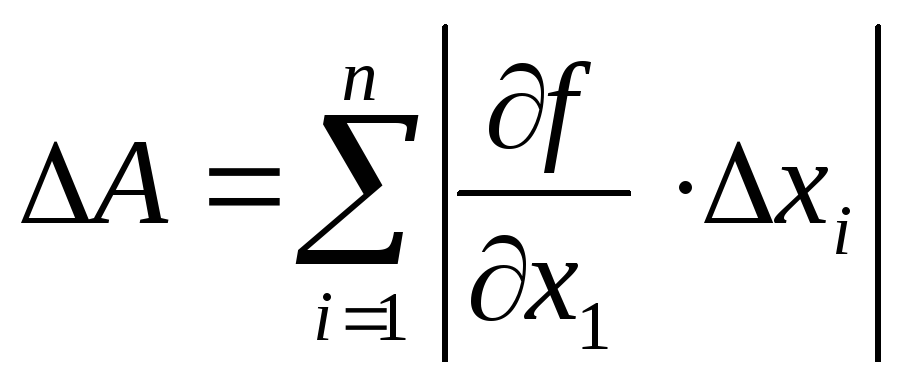(18)

а для расчёта
предельной относительной ошибки пригодна
фор

— 19 —

мула:

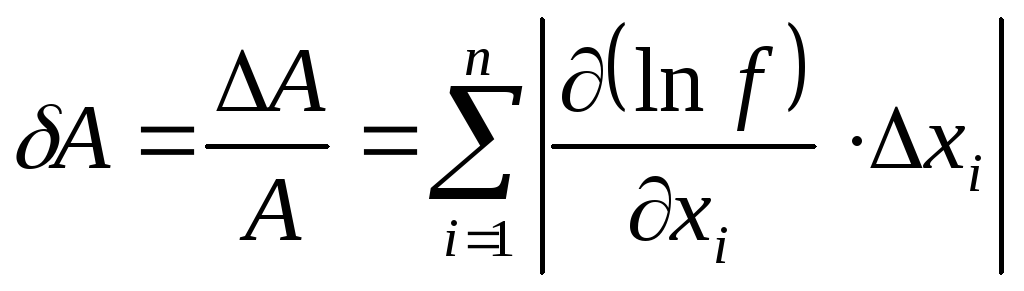(19)

Формулы для расчёта
предельных ошибок некоторых часто
встречающихся функций, когда приборные
ошибки превышают случайные, приведены
в Таблице 2. Эти выражения легко
рассчитываются по формулам (18) и (19).

2-й случай. Преобладают
случайные ошибки. Для определения
среднеквадратичной ошибки теория
вероятностей даёт следующую формулу:

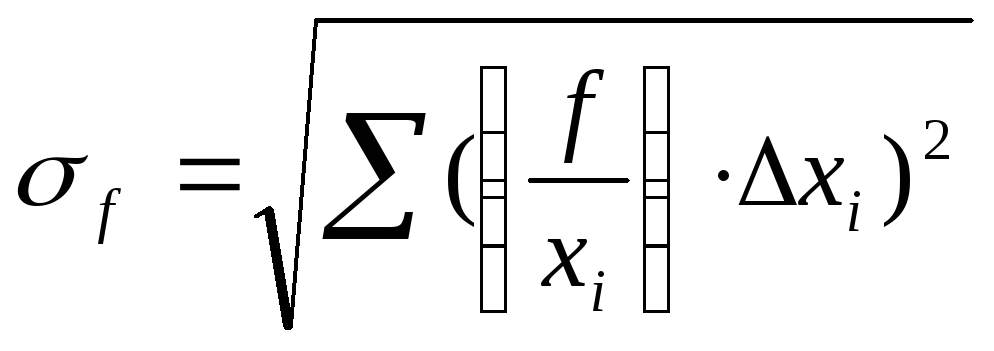(20)

Относительная
ошибка вычисляется по формуле:

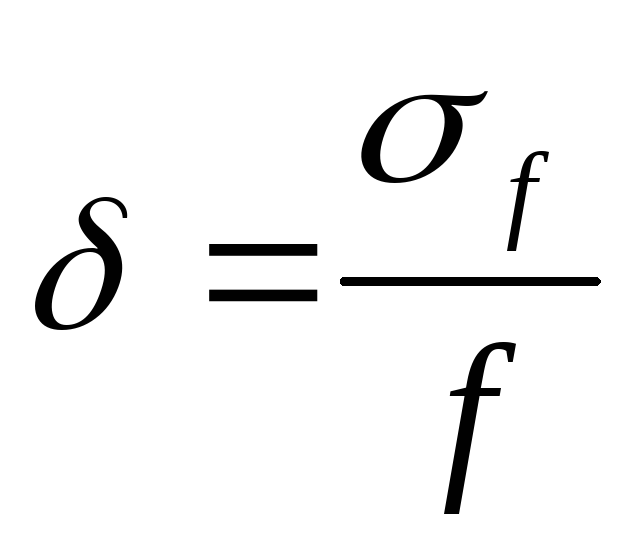(21)

При выполнении
промежуточных расчётов необходимо
помнить, что число точных цифр в результате
расчётов не может увеличиваться. Поэтому
промежуточные результаты округляют,
сохраняя

1…2 избыточных
знака. При этом последующие цифры,
меньшие

5,отбрасываются;если
первая из отбрасываемых цифр больше 5,

то последняя из
оставшихся цифр увеличивается на
единицу. Ес

ли первая
отбрасываемая цифра 5, то предыдущая
цифра остаётся

без изменений,
если она чётная, и увеличивается на
единицу, если

она нечётная.
Выражения для среднеквадратичной ошибки
некоторых часто встречающихся функций
приведены в Таблице 3. Для определения
ошибок косвенных измерений используют
большую из инструментальной или случайной
ошибок прямого измерения.

ВЕСА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ

При неравноточных измерениях, когда результаты каждого измерения нельзя считать одинаково надежными, уже нельзя обойтись определением простого арифметического среднего. В таких случаях учитывают достоинство (или надежность) каждого результата измерений.Достоинство результатов измерений выражают некоторым числом, называемым весом этого измерения. Очевидно, что арифметическое среднее будет иметь больший вес по сравнению с единичным измерением, а измерения, выполненные при использовании более совершенного и точного прибора, будут иметь большую степень доверия, чем те же измерения, выполненные прибором менее точным.
Поскольку условия измерений определяют различную величину средней квадратической погрешности, то последнюю и принято принимать в качестве основы оценки весовых значений, проводимых измерений. При этом веса результатов измерений принимают обратно пропорциональными квадратам соответствующих им средних квадратических погрешностей.
Так, если обозначить через р и Р веса измерений, имеющие средние квадратические погрешности соответственно m и µ, то можно записать соотношение пропорциональности:

Например, если µ средняя квадратическая погрешность арифметического среднего, а m – соответственно, одного измерения, то, как следует из

можно записать:

т. е. вес арифметического среднего в n раз больше веса единичного измерения.

Аналогичным образом можно установить, что вес углового измерения, выполненного 15-секундным теодолитом, в четыре раза выше веса углового измерения, выполненного 30-секундным прибором.

При практических вычислениях обычно вес одной какой-либо величины принимают за единицу и при этом условии вычисляют веса остальных измерений. Так, в последнем примере если принять вес результата углового измерения 30-секундным теодолитом за р = 1, то весовое значение результата измерения 15-секундным теодолитом составит Р = 4.

Понятие и классификация

Под термином погрешность принято понимать степень отклонения реальной величины от вычисленной. Этот показатель служит мерой точности измерения.

Существует несколько разновидностей погрешности:

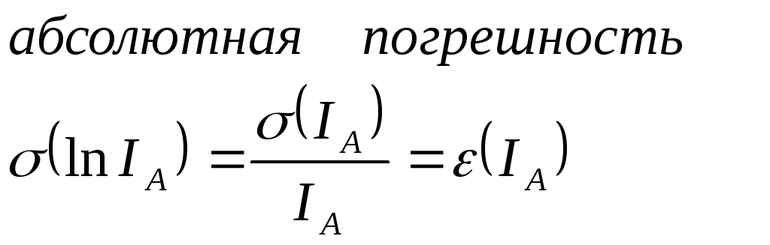
1. Абсолютная — оценка ошибки в абсолютных единицах. Величина ее может быть разной в зависимости от способа расчета.
2. Относительная — отношение абсолютной величины к тому значению, которое принято считать истинным. Измеряется в процентах.
3. Приведенная — разновидность относительной. Ее вычисляют отношением абсолютной и условной постоянной величины, определяется в процентах.
4. Приборная или инструментальная — погрешность, которую дают технические средства измерений. Она обусловлена неточной цифровой градуировкой приборов или недостаточной наглядностью. Класс точности приборов будет равен максимальной приведенной погрешности и выражается в процентах. К примеру, класс точности вольтметра ΔU = ±0,75 В.
5. Методическая — связанная с несовершенством метода измерения или его чрезмерным упрощением.
6. Субъективная или операторная — погрешность, связанная с личными свойствами оператора — невнимательностью, утомлением, профессиональной подготовленностью.
7. Случайная. Погрешность, которая может изменяться при разных измерениях. Изменения возможны по знаку или величине отклонения. Причиной может быть техническое несовершенство приборов отсчета или объекта измерения, неблагоприятные для работы условия или особенности измеряемых единиц.
8. Систематическая. Погрешность, изменения которой имеют некоторую закономерность во времени. В качестве частного случая допускают постоянное отклонение, которое не изменяется во времени.
9. Прогрессирующая или дрейфовая — медленно изменяется во времени и не может быть предсказана. Такое отклонение относится к случайным.
10. Грубая или промах. Значительное отклонение от принятой нормы. Возникает в результате неисправности аппаратуры или ошибки экспериментатора.

Абсолютная погрешность — измерительный прибор

Абсолютная погрешность измерительного прибора представляет собой расхождение ( разность) между измеренным Ли и действительным ( истинным) Лд значениями измеряемой величины ДЛ — / 4н — Ац. Истинное значение измеряемой величины находят с учетом поправки. Поправка — это величина, обратная по знаку абсолютной погрешности: ДР — ДЛ Ал-А. Абсолютная погрешность электроизмерительных приборов со стрелочным показателем практически неизменна в пределах всей шкалы, поэтому с уменьшением значения измеряемой величины она возрастает. Для повышения точности измерения измеряемой величины на показывающих приборах со стрелочным указателем следует выбирать такие пределы измерения, чтобы отсчитывать показания примерно в пределах 2 / 3 всей шкалы.
 

Абсолютная погрешность измерительного прибора равна разности между показанием прибора и действительным ( точным) значением измеряемой величины.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и истинным значением измеряемой величины. Погрешность показаний прибора имеет своими источниками погрешности отдельных его элементов: чувствительного элемента, передаточного механизма и шкалы. Погрешность чувствительного элемента заключается в том, что действительная зависимость его перемещений от измеряемой величины не совпадает с расчетной, заложенной в схему прибора. Погрешность шкалы складывается из ошибки положения ее штрихов и эксцентриситета шкалы.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Так как истинное значение измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Поскольку последнее установить нельзя, то в измерительной технике используют так называемое действительное значение, полученное посредством образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины Так как величину истинного значения измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Приведенная погрешность измерительного прибора — отношение абсолютной погрешности измерительного прибора к нормирующему значению, выраженное в процентах.
 

Корректность поставленных экспериментов доказана отсутствием превышения абсолютных ошибок измерения как при определении перемещений, так и напряжений над абсолютной погрешностью используемых измерительных приборов.
 

В некоторых случаях ( для образцовых и рабочих средств измерений повышенной точности) для исключения систематической погрешности показаний вводят поправку, равную абсолютной погрешности измерительного прибора.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и действительным значением измеряемой величины.
 

В данном разделе будут рассмотрены виды погрешностей, свойственные мерам, отдельным элементам и устройствам, а также средствам измерений в целом. Под абсолютной погрешностью меры понимают разность ( отклонение от номинального значения) между номинальным значением меры и истинным значением воспроизводимой ею величины. Так как истинное значение величины остается неизвестным, то на практике вместо него используют действительное значение величины. Следует различать абсолютную погрешность измерительного преобразователя по входу и по выходу. Абсолютную погрешность измерительного преобразователя по входу находят как разность между значением величины на входе преобразователя, определяемой в принципе по истинному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и истинным значением величины на входе преобразователя. Абсолютную погрешность измерительного преобразователя по выходу находят как разность между истинным значением величины на выходе преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемой в принципе по истинному значению величины на выходе с помощью градуировочной характеристики, приписанной преобразователю. Относительная погрешность измерительного прибора определяется как отношение абсолютной погрешности измерительного прибора к истинному значению измеряемой им величины.
 

Методики расчета

Существует несколько методов определения отклонения. Наиболее простой и доступный способ:

Необходимые измерения проводят не менее 5 раз. Это дает возможность вычислить наиболее точное значение параметра. Результаты вносят в таблицу excel.
Полученные величины складывают и делят на количество замеров. В результате получится действительное значение. Его обычно применяют вместо истинного, так как нет возможности вычислить последнее.
Следующий шаг — определение абсолютной погрешности. Ее считают для каждого измерения. Чтобы узнать величину этого показателя, из результата каждого замера вычитают действительное значение

Для обработки данных неважно, положительная или отрицательная получилась цифра. Используют модули полученных чисел, пренебрегая знаками.
Чтобы определить относительную погрешность измерения, нужно разделить абсолютную на действительное значение. Полученное число умножают на 100%.

Полученное число умножают на 100%.

Для определения предельного отклонения выбирают наибольшее значение из всех полученных.

Чтобы получить наиболее точные показатели дискретности цифровых приборов, пользуются средним квадратическим отклонением. Вычислить его можно следующим способом:

1. Каждый показатель абсолютной погрешности возводят в квадрат и записывают.
2. Полученные результаты складывают между собой.
3. Сумму всех квадратов делят на число, которое на единицу меньше количества измерений.
4. Из результата вычислений извлекают квадратный корень — это и будет среднее квадратическое отклонение.

Чтобы вычислить, чему равна относительная погрешность измерения, важно придерживаться некоторых правил. Складывая или вычитая числа, учитывают абсолютные отклонения. Если числа нужно разделить или перемножить, прибегают к относительным показателям

Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.

Если числа нужно разделить или перемножить, прибегают к относительным показателям. Возведение числа в степень требует умножить относительную погрешность на показатель этой степени.

Результаты фиксируются в виде десятичных дробей. Точное значение может быть очень длинным, вплоть до бесконечного. Для удобства используют только среднее значение

При этом важно помнить о существовании верных и сомнительных цифр. У первой категории цифр разряд бывает выше допустимой погрешности, у второй — ниже.. При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%

Эта же закономерность применяется для оценки температуры и других физических величин.

При расчете относительной погрешности измерения времени формула включает в себя отношение среднего отклонения к среднему значению времени, умноженное на 100%. Эта же закономерность применяется для оценки температуры и других физических величин.

Абсолютная и относительная погрешность

Абсолютной погрешностью или, короче, погрешностью приближенного
числа называется разность между этим числом и его точным значением (из большего числа вычитается меньшее)*.

Пример 1. На предприятии 1284 рабочих и служащих. При
округлении этого числа до 1300 абсолютная погрешность
составляет 1300 — 1284 = 16. При округлении до 1280 абсолютная погрешность составляет 1284 — 1280 = 4.

Относительной погрешностью приближенного числа называется отношение
абсолютной погрешности приближенного числа к самому этому числу.

Пример 2. В школе 197 учащихся. Округляем это число до 200. Абсолютная
погрешность составляет 200 — 197 = 3. Относительная погрешность равна 3/197 или, округленно, 3/197 = 1,5 %.

В большинстве случаев невозможно узнать точное значение приближенного числа, а значит, и точную величину погрешности.
Однако почти всегда можно установить, что погрешность (абсолютная или относительная) не превосходит некоторого числа.

Пример 3. Продавец взвешивает арбуз на чашечных весах. В наборе гирь наименьшая — 50 г. Взвешивание дало 3600 г. Это число – приближенное. Точный вес арбуза
неизвестен. Но абсолютная погрешность не
превышает 50 г. Относительная погрешность не превосходит 50/3600 ≈ 1,4%.

Число, заведомо превышающее абсолютную погрешность (или в худшем случае равное ей), называется предельной абсолютной погрешностью. Число, заведомо превышающее
относительную погрешность (или в худшем случае равное ей), называется предельной относительной погрешностью.

В примере 3 за предельную абсолютную погрешность можно взять 50 г, а за предельную относительную погрешность — 1,4 %.

Величина предельной погрешности не является вполне определенной. Так, в примере 3 можно принять за предельную абсолютную
погрешность 100 г, 150 г и вообще всякое число, большее чем 50 г. На практике берется по возможности меньшее значение
предельной погрешности. В тех случаях, когда известна точная величина погрешности, эта величина служит одновременно
предельной погрешностью. Для каждого приближенного числа должна быть известна его предельная погрешность
(абсолютная или oотносительная). Когда она прямо не указана, подразумевается что предельная абсолютная погрешность
составляет половину единицы последнего выписанного разряда. Так, если приведено приближенное число 4,78 без указания
предельной погрешности, то подразумевается, что предельная абсолютная погрешность составляет 0,005. Вследствие этого
соглашения всегда можно обойтись без указания предельной погрешности числа.

Предельная абсолютная погрешность обозначается греческой буквой Δ («дельта»); предельная относительная
погрешность — греческой буквой δ («дельта малая»). Если приближенное число обозначить буквой а, то

δ = Δ/a.

Пример 4. Длина карандаша измерена линейкой с миллиметровыми делениями. Измерение показало 17,9 см. Какова предельная
относительная погрешность этого измерения?
Здесь а = 17,9 см; можно принять Δ = 0,1 см, так как с точностью до 1 мм измерить карандаш нетрудно, a значительно уменьшить, предельную погрешность ни удастся (при навыке можно прочесть на хорошей линейке и 0,02 и даже 0,01 см, но у самого карандаша ребра могут разниться на бoльшую величину). Относительная погрешность равна 0,1/17,9.
Округляя, находим δ = 0,1/18 ≈ 0,6%.

Пример 5. Цилиндрический поршень имеет около 35 мм в диаметре. С какой точностью нужно его измерить микрометром, чтобы
предельная относительная погрешность составляла 0,05%?Решение. По условию, предельная абсолютная погрешность должна составлять 0,05% от 35 мм. Следовательно, предельная
абсолютная погрешность равна 36*(0,05/100) = 0,0175 (мм) или, усиливая, 0,02 (мм). Можно воспользоваться
формулой δ = Δ/a.
Подставляя в неё а = 35, δ = 0,0005, имеем 0,0005 = Δ/35. Значит, Δ = 35 • 0,0005 = 0,0175 (мм).

* Иначе говоря, если a есть приближенное число, а х – его точное значение, то абсолютная погрешность есть абсолютное
значение разности a – х. В некоторых руководствах абсолютной погрешностью называется сама
разность a – х (или разность х — a). Эта величина может быть положительной или отрицательной.

Абсолютная и относительная погрешности

Точность полученного в результате вычисления результата определяется погрешностью вычислений. Различают два вида погрешностей – абсолютную и относительную.

Абсолютная погрешность некоторого числа равна разности между его истинным значением и приближенным значением, полученным в результате вычисления или измерения:

          (А.1)

где а – приближенное значение числа х.

Относительная погрешность – это отношение абсолютной погрешности к приближенному значению числа:

           (А.2)

Истинное значение величины х обычно неизвестно. Имеется лишь приближенное значение а и нужно найти его предельную погрешность . В дальнейшем значение  принимается в качестве абсолютной погрешности приближенного числа а. Тогда истинное значение х находится в интервале .

ПОГРЕШНОСТИ ИЗМЕРЕНИЙ

При многократном измерении одной и той же величины каждый раз получают несколько отличающиеся результаты, как по абсолютной величине, так и по знакам, каким бы опытом не обладал исполнитель и какими бы высокоточными приборами он не пользовался.
Погрешности различают: грубые, систематические и случайные.
Появление грубых погрешностей (промахов) связано с серьезными ошибками при производстве измерительных работ. Эти ошибки легко выявляются и устраняются в результате контроля измерений.Систематические погрешностивходят в каждый результат измерений по строго определенному закону. Они обусловлены влиянием конструкции измерительных приборов, погрешностями градуировки их шкал, износом и т. д. (инструментальные погрешности)иливозникают из-за недоучета условий измерений и закономерностей их изменений, приближенности некоторых формул и др. (методические погрешности). Систематические погрешности делятся на постоянные (неизменные по знаку и вели чине) и переменные (изменяющие свою величину от одного измерения к другому по определенному закону).
Такие погрешности заранее определимы и могут быть сведены к необходимому минимуму путем введения соответствующих поправок.Например, заранее может быть учтено влияние кривизны Земли на точность определения вертикальных расстояний, влияние температуры воздуха и атмосферного давления при определении длин линий светодальномерами или электронными тахеометрами, заранее можно учесть влияние рефракции атмосферы и т. д.
Если не допускать грубых погрешностей и устранять систематические, то качество измерений будет определяться только случайными погрешностями. Эти погрешности неустранимы, однако их поведение подчиняется законам больших чисел. Их можно анализировать, контролировать и сводить к необходимому минимуму.
Для уменьшения влияния случайных погрешностей на результаты измерений прибегают к многократным измерениям, к улучшению условий работы, выбирают более совершенные приборы, методы измерений и осуществляют тщательное их производство.
Сопоставляя ряды случайных погрешностей равноточных измерений можно обнаружить, что они обладают следующими свойствами:
а) для данного вида и условий измерений случайные погрешности не могут превышать по абсолютной величине некоторого предела;
б) малые по абсолютной величине погрешности появляются чаще больших;
в) положительные погрешности появляются так же часто, как и равные им по абсолютной величине отрицательные;
г) среднее арифметическое из случайных погрешностей одной и той же величины стремится к нулю при неограниченном увеличении числа измерений.
Распределение ошибок, соответствующее указанным свойствам, называется нормальным (рис. 12.1).

Рис. 12.1. Кривая нормального распределения случайных погрешностей Гаусса

Разность между результатом измерения некоторой величины (l) и ее истинным значением (X) называют абсолютной (истинной) погрешностью.

Δ = l — X

Истинное (абсолютно точное) значение измеряемой величины получить невозможно, даже используя приборы самой высокой точности и самую совершенную методику измерений. Лишь в отдельных случаях может быть известно теоретическое значение величины. Накопление погрешностей приводит к образованию расхождений между результатами измерений и действительными их значениями.Разность суммы практически измеренных (или вычисленных) величин и теоретического ее значения называется невязкой. Например, теоретическая сумма углов в плоском треугольнике равна 180º, а сумма измеренных углов оказалась равной 180º02′; тогда погрешность суммы измеренных углов составит +0º02′. Эта погрешность будет угловой невязкой треугольника.
Абсолютная погрешность не является, полным показателем точности выполненных работ. Например, если некоторая линия, фактическая длина которой составляет 1000 м, измерена землемерной лентой с ошибкой 0,5 м, а отрезок длиною 200 м  – с ошибкой 0,2 м, то, несмотря на то, что абсолютная погрешность первого измерения больше второго, все же первое измерение было выполнено с точностью в два раза более высокой. Поэтому вводят понятие относительной погрешности:

Отношение абсолютной погрешности измеряемой величины Δ к измеренной величине l называют относительной погрешностью.

Относительные погрешности всегда выражаются дробью с числителем, равным единице (аликвотная дробь). Так, в приведенном выше примере относительная погрешность первого измерения составляет

,

а второго 

Абсолютная погрешность — измерительный прибор

Абсолютная погрешность измерительного прибора представляет собой расхождение ( разность) между измеренным Ли и действительным ( истинным) Лд значениями измеряемой величины ДЛ — / 4н — Ац. Истинное значение измеряемой величины находят с учетом поправки. Поправка — это величина, обратная по знаку абсолютной погрешности: ДР — ДЛ Ал-А. Абсолютная погрешность электроизмерительных приборов со стрелочным показателем практически неизменна в пределах всей шкалы, поэтому с уменьшением значения измеряемой величины она возрастает. Для повышения точности измерения измеряемой величины на показывающих приборах со стрелочным указателем следует выбирать такие пределы измерения, чтобы отсчитывать показания примерно в пределах 2 / 3 всей шкалы.
 

Абсолютная погрешность измерительного прибора равна разности между показанием прибора и действительным ( точным) значением измеряемой величины.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и истинным значением измеряемой величины. Погрешность показаний прибора имеет своими источниками погрешности отдельных его элементов: чувствительного элемента, передаточного механизма и шкалы. Погрешность чувствительного элемента заключается в том, что действительная зависимость его перемещений от измеряемой величины не совпадает с расчетной, заложенной в схему прибора. Погрешность шкалы складывается из ошибки положения ее штрихов и эксцентриситета шкалы.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Так как истинное значение измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Поскольку последнее установить нельзя, то в измерительной технике используют так называемое действительное значение, полученное посредством образцового прибора.
 

Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины Так как величину истинного значения измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
 

Приведенная погрешность измерительного прибора — отношение абсолютной погрешности измерительного прибора к нормирующему значению, выраженное в процентах.
 

Корректность поставленных экспериментов доказана отсутствием превышения абсолютных ошибок измерения как при определении перемещений, так и напряжений над абсолютной погрешностью используемых измерительных приборов.
 

В некоторых случаях ( для образцовых и рабочих средств измерений повышенной точности) для исключения систематической погрешности показаний вводят поправку, равную абсолютной погрешности измерительного прибора.
 

Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и действительным значением измеряемой величины.
 

В данном разделе будут рассмотрены виды погрешностей, свойственные мерам, отдельным элементам и устройствам, а также средствам измерений в целом. Под абсолютной погрешностью меры понимают разность ( отклонение от номинального значения) между номинальным значением меры и истинным значением воспроизводимой ею величины. Так как истинное значение величины остается неизвестным, то на практике вместо него используют действительное значение величины. Следует различать абсолютную погрешность измерительного преобразователя по входу и по выходу. Абсолютную погрешность измерительного преобразователя по входу находят как разность между значением величины на входе преобразователя, определяемой в принципе по истинному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и истинным значением величины на входе преобразователя. Абсолютную погрешность измерительного преобразователя по выходу находят как разность между истинным значением величины на выходе преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемой в принципе по истинному значению величины на выходе с помощью градуировочной характеристики, приписанной преобразователю. Относительная погрешность измерительного прибора определяется как отношение абсолютной погрешности измерительного прибора к истинному значению измеряемой им величины.