Виды погрешностей
Содержание:
Введение
Все, что сказано в этом введении, запоминать не нужно. это справочный материал, к которому вы будете обращаться при выполнении лабораторных работ.
1. Как определять погрешности измерений
Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.
Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.
Прямое измерение — определение значения физической величины непосредственно средствами измерения.
Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.
Введем следующие обозначения:
A, B, C, … — физические величины.
Aпр — приближенное значение физической величины, т.е. значение, полученное путем прямых или косвенных измерений.
ΔA — абсолютная погрешность измерения физической величины.
ε — относительная погрешность измерения физической величины, равная:
ΔиA — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; указывается в каждой работе при описании прибора в разделе Оборудование и средства измерения)
ΔоA — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения), она равна в большинстве случаев половине цены деления; при измерении времени — цене деления секундомера или часов.
Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:
ΔA=ΔиA + ΔоA
Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔA≈0,17=0,2); численное значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А=10,332≈10,3).
Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, отличаются друг от друга.
В этом случае Aпр находят как среднее арифметическое значение всех измерений, а ΔA (ее в этом случае называют случайной погрешностью) определяют методами математической статистики.
В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. При этом для получения результата достаточно одного измерения.
Относительная погрешность косвенных измерений определяется, как показано в таблице 1.
Абсолютная погрешность косвенных измерений определяется по формуле ΔA=Aпрε (ε выражается десятичной дробью).
Таблица 1
Формулы для нахождения относительной погрешности косвенных измерений
| Nº п/п | Формула физической величины | Формула относительной погрешности |
|---|---|---|
| 1 | ||
| 2 | ||
| 3 |
A=B+C |
|
| 4 |
2. О классе точности электроизмерительных приборов
Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γпр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность ΔиA от всей шкалы прибора (Amax):
Класс точности указывается при описании прибора в разделе Оборудование и средства измерения. Cуществуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γпр) и всю его шкалу (Amax), определяют абсолютную погрешность ΔиA измерения физической величины А этим прибором:
3. Как сравнивать результаты измерений
1. Записать результаты измерений в виде двойных неравенств:
A1 пр – ΔA1 < A1 пр < A1 пр + ΔA1A2 пр – ΔA2 < A2 пр < A2 пр + ΔA2
2. Сравнить полученные интервалы значений (рис.1): если интервалы не перекрываются, то результаты неодинаковы, если перекрываются — одинаковы при данной относительной погрешности измерений.
 Рисунок 1.
Рисунок 1.
4. Как оформлять отчет о проделанной работе
Отчетом о проделанной работе является форма, находящаяся в левом нижнем окне. После ее заполнения надо нажать на кнопку «Отправить результаты на сервер».
Значения измеренных физических величин переносятся в таблицу результатов автоматически после нажатия соответствующей кнопки.
Значения остальных величин и ответ на контрольный вопрос вводятся с клавиатуры.
домашней странице BARSIC
Приведенная относительная погрешность
Приведенная относительная погрешность прибора — это погрешность, выраженная в процентах от его предела измерения. Ее вычисляют или от суммы верхнего и нижнего пределов измерения, если прибор имеет двухстороннюю шкалу измерения ( с нулевой отметкой в середине шкалы), или от разности пределов при односторонней шкале.
Наибольшая основная приведенная относительная погрешность, выраженная в процентах, характеризует класс точности прибора.
Приведенную относительную погрешность для приборов со шкалой, начинающейся от нулевого значения измеряемой величины, определяют в процентах от верхнего предела измерения, для приборов с безнулевой шкалой — от среднего арифметического пределов измерения, а для приборов с двусторонней шкалой — от суммы пределов измерения.
Приведенной относительной погрешностью называется отношение абсолютной погрешности к максимальному значению выходной величины, определяющему диапазон ее изменения.
При постоянной приведенной относительной погрешности прибора относительная погрешность измерения возрастает с уменьшением измеряемой величины.
Допустимая величина приведенной относительной погрешности едол определяет класс точности прибора, указываемый на его шкале. По ГОСТ 1845 — 59 предусматриваются следующие классы точности электроизмерительных приборов: 0 05; 0 1; 0 2; 0 5; 1 0; 1 5; 2 5; 4 0 и классы 0 02; 0 05; 0 1; 0 2; 0 5; 1 0 для шунтов и добавочных сопротивлений к приборам.
Используется также оценка приведенной относительной погрешности ( отн.
|
Прибор с зеркальной шкалой. / — шкала. 2 -стрелка. Л — зеркало.| Нопиуеиая шкала. |
Завод-изготовитель гарантирует, что наибольшая приведенная относительная погрешность прибора в пределах рабочей части его шкалы не превышает определенного значения, называемого допустимой п о г р е ш-н о с т ь ю прибора.
При постоянстве абсолютной погрешности Ду приведенная относительная погрешность b также постоянна.
Приборы класса 0 1 ( допустимая приведенная относительная погрешность 0 1 %), как правило, являются лабораторными.
Класс точности прибора характеризуется величиной приведенной относительной погрешности. Большинство радиоизмерительных приборов на классы не делят, так как применяемые стрелочные индикаторы используют совместно с соответствующей электронной схемой.
|
Схема опре деления погрешности. |
Обычно для оценки точности элементов используется приведенная относительная погрешность.
При постоянстве абсолютной погрешности Дг / приведенная относительная погрешность b также постоянна.
Какие классы точности бывают, как обозначаются
Как мы уже успели выяснить, интервал погрешности определяется классом точности. Данная величина рассчитывается, устанавливается ГОСТом и техническими условиями. В зависимости от заданной погрешность, бывает: абсолютная, приведенная, относительная, см. таблицу ниже

Согласно ГОСТ 8.401-80 в системе СИ классы точности обычно помечается латинской буквой, часто с добавлением индекса, отмеченного цифрой. Чем меньше погрешность, соответственно, меньше цифра и буквенное значение выше по алфавиту, тем более высокая точность.
Приборы, способные выполнять множество различных замеров, могут быть одновременно более двух классов.
Класс точности обозначается на корпусе устройства в виде числа обведенного в кружок, обозначает диапазон погрешностей измерений в процентах. Например, цифра ② означает относительную погрешность ±2%. Если рядом со знаком присутствует значок в виде галочки, это значит, что длина шкалы используется в качестве вспомогательного определения погрешности.

- 0,1, 0,2 – считается самым высоким классом
- 0,5, 1 – чаще применяется для устройств средней ценовой категории, например, бытовых
- 1,5, 2,5 – используется для приборов измерения с низкой точностью или индикаторов, аналоговых датчиков
Примечание. На корпусе высокоточных измерителей, класс может не наносится. Обозначение таких устройств как правило выполняется особыми знаками.
ВЕСА РЕЗУЛЬТАТОВ НЕРАВНОТОЧНЫХ ИЗМЕРЕНИЙ
При неравноточных измерениях, когда результаты каждого измерения нельзя считать одинаково надежными, уже нельзя обойтись определением простого арифметического среднего. В таких случаях учитывают достоинство (или надежность) каждого результата измерений.Достоинство результатов измерений выражают некоторым числом, называемым весом этого измерения. Очевидно, что арифметическое среднее будет иметь больший вес по сравнению с единичным измерением, а измерения, выполненные при использовании более совершенного и точного прибора, будут иметь большую степень доверия, чем те же измерения, выполненные прибором менее точным.
Поскольку условия измерений определяют различную величину средней квадратической погрешности, то последнюю и принято принимать в качестве основы оценки весовых значений, проводимых измерений. При этом веса результатов измерений принимают обратно пропорциональными квадратам соответствующих им средних квадратических погрешностей.
Так, если обозначить через р и Р веса измерений, имеющие средние квадратические погрешности соответственно m и µ, то можно записать соотношение пропорциональности:
Например, если µ средняя квадратическая погрешность арифметического среднего, а m – соответственно, одного измерения, то, как следует из
можно записать:
т. е. вес арифметического среднего в n раз больше веса единичного измерения.
Аналогичным образом можно установить, что вес углового измерения, выполненного 15-секундным теодолитом, в четыре раза выше веса углового измерения, выполненного 30-секундным прибором.
При практических вычислениях обычно вес одной какой-либо величины принимают за единицу и при этом условии вычисляют веса остальных измерений. Так, в последнем примере если принять вес результата углового измерения 30-секундным теодолитом за р = 1, то весовое значение результата измерения 15-секундным теодолитом составит Р = 4.
Абсолютная погрешность — измерительный прибор
Абсолютная погрешность измерительного прибора представляет собой расхождение ( разность) между измеренным Ли и действительным ( истинным) Лд значениями измеряемой величины ДЛ — / 4н — Ац. Истинное значение измеряемой величины находят с учетом поправки. Поправка — это величина, обратная по знаку абсолютной погрешности: ДР — ДЛ Ал-А. Абсолютная погрешность электроизмерительных приборов со стрелочным показателем практически неизменна в пределах всей шкалы, поэтому с уменьшением значения измеряемой величины она возрастает. Для повышения точности измерения измеряемой величины на показывающих приборах со стрелочным указателем следует выбирать такие пределы измерения, чтобы отсчитывать показания примерно в пределах 2 / 3 всей шкалы.
Абсолютная погрешность измерительного прибора равна разности между показанием прибора и действительным ( точным) значением измеряемой величины.
Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и истинным значением измеряемой величины. Погрешность показаний прибора имеет своими источниками погрешности отдельных его элементов: чувствительного элемента, передаточного механизма и шкалы. Погрешность чувствительного элемента заключается в том, что действительная зависимость его перемещений от измеряемой величины не совпадает с расчетной, заложенной в схему прибора. Погрешность шкалы складывается из ошибки положения ее штрихов и эксцентриситета шкалы.
Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Так как истинное значение измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины. Поскольку последнее установить нельзя, то в измерительной технике используют так называемое действительное значение, полученное посредством образцового прибора.
Абсолютной погрешностью измерительного прибора называется разность между его показанием и истинным значением измеряемой величины Так как величину истинного значения измеряемой величины установить нельзя, в измерительной технике используется так называемое действительное значение, полученное с помощью образцового прибора.
Приведенная погрешность измерительного прибора — отношение абсолютной погрешности измерительного прибора к нормирующему значению, выраженное в процентах.
Корректность поставленных экспериментов доказана отсутствием превышения абсолютных ошибок измерения как при определении перемещений, так и напряжений над абсолютной погрешностью используемых измерительных приборов.
В некоторых случаях ( для образцовых и рабочих средств измерений повышенной точности) для исключения систематической погрешности показаний вводят поправку, равную абсолютной погрешности измерительного прибора.
Абсолютная погрешность измерительного прибора определяется разностью между показанием прибора и действительным значением измеряемой величины.
В данном разделе будут рассмотрены виды погрешностей, свойственные мерам, отдельным элементам и устройствам, а также средствам измерений в целом. Под абсолютной погрешностью меры понимают разность ( отклонение от номинального значения) между номинальным значением меры и истинным значением воспроизводимой ею величины. Так как истинное значение величины остается неизвестным, то на практике вместо него используют действительное значение величины. Следует различать абсолютную погрешность измерительного преобразователя по входу и по выходу. Абсолютную погрешность измерительного преобразователя по входу находят как разность между значением величины на входе преобразователя, определяемой в принципе по истинному значению величины на его выходе с помощью градуировочной характеристики, приписанной преобразователю, и истинным значением величины на входе преобразователя. Абсолютную погрешность измерительного преобразователя по выходу находят как разность между истинным значением величины на выходе преобразователя, отображающей измеряемую величину, и значением величины на выходе, определяемой в принципе по истинному значению величины на выходе с помощью градуировочной характеристики, приписанной преобразователю. Относительная погрешность измерительного прибора определяется как отношение абсолютной погрешности измерительного прибора к истинному значению измеряемой им величины.
Основная приведенная погрешность — прибор
Основная приведенная погрешность прибора 1 5 % относительно конца шкалы.
|
Датчик анализатора ЛКВЛ-Л. |
Основная приведенная погрешность прибора равна 5 % от данного диапазона измерения.
Основная приведенная погрешность прибора не превышает 1 5 % на поддиапазонах 100, 200, 500 щ и 1 2, 5, 10, 20, 50, 100 кгц и 2 % на поддиапазоне 200 кгц.
Основная приведенная погрешность прибора — погрешность, приведенная к верхнему ( или номинальному) пределу измерения и определенная для нормальных условий.
Основная приведенная погрешность прибора не превышает 0 5 % от нормирующего значения измеряемой величины. Длина шкалы прибора равна 160 мм. В приборе размещено восемь переключаемых шкал различных градуировок. Время прохождения указателем всей шкалы не превышает 2 5 с. Время переключения шкал с первой на восьмую не превышает 2 с.
|
Практическая система электрических единиц. |
Основной приведенной погрешностью прибора называется выраженное в процентах отношение абсолютной погрешности к наибольшему значению, которое может быть замерено по шкале прибора.
После ремонта и тарировки проверяют основную приведенную погрешность прибора, которая не должна превышать 1 6 % в интервале температур 5 — 50е С. Прибор проверяют в начальной, конечной и 3 — 4 — х промежуточных точках шкалы. Поверку приборов с верхним пределом измерения менее 0 4 Мн / м ( 4 кгс / см) выполняют с помощью сжатого воздуха.
Класс точности прибора означает в частности, что основная приведенная погрешность прибора ( положительная или отрицательная) в рабочем диапазоне шкалы, выраженная в процентах, не превышает значения, соответствующего классу прибора. ГОСТ 1845 — 59 нормирует и дополнительные погрешности приборов.
Для отнесения СЭП к определенному классу точности необходимо, чтобы основная приведенная погрешность прибора, определенная опытным путем, не выходила за пределы зоны, ограниченной предельными значениями К ( %), где К — значение класса точности.
На шкалах приборов числа, указывающие класс точности, обозначают основные приведенные погрешности приборов.
Для амперметров, вольтметров и ваттметров, рассматриваемых в данной главе, класс точности численно равен пределу допускаемой основной приведенной погрешности прибора.
Как видно, средняя квадратичная погрешность измерения перепада adh обратно пропорциональна величине измеряемого перепада и уже при перепаде, равном V3 предельного значения, становится численно равной основной приведенной погрешности прибора. Поэтому и относительная погрешность измерения расхода по методу переменного перепада быстро возрастает по мере уменьшения относительной величины измеряемого расхода. При расходах менее 30 % предельного точность измерения становится недостаточной.
Вольтметр типа ВК7 — 4 ( ВОЛУ-1), в котором приняты все указанные выше меры, может применяться в частотном диапазоне от 20 гц до 700 Мгц. Согласно паспортным данным основная приведенная погрешность прибора, равная 2 5 %, определяется на частоте 1 000 гц.
Приведенная погрешность
Приведенная погрешность, как и относительная, является безразмерной величиной и обычно выражается в процентах. Кроме того, она пропорциональна абсолютной погрешности. Поэтому если абсолютная погрешность измерительного преобразователя постоянна во всем диапазоне измерения, то приведенная будет также постоянной. Следовательно, она характеризует точность измерительного преобразователя независимо от значения измеряемого параметра и ее считают основной метрологии ческой характеристикой измерительного преобразователя.
Приведенная погрешность определяет класс точности приборов.
Приведенная погрешность является удобной обобщенной характеристикой, свободной от перечисленных выше недостатков. Она определяется лишь качеством изготовления измерительного механизма и отсчетного устройства прибора и не зависит ни от диапазона измерения, ни от значения измеряемой величины.
Приведенная погрешность для данного прибора задана и постоянна по всей шкале. На это значение и следует ориентироваться при выборе образцовой меры.
Приведенная погрешность является важнейшей характеристикой измерительного прибора, так как именно она используется для объективной оценки метрологических качеств прибора.
Приведенная погрешность положена в основу определения класса точности приборов. Она лишь косвенно характеризует точность измерения.
Приведенная погрешность выражается в процентах, но не является относительной погрешностью.
Приведенная погрешность определяется для статического ( установившегося) режима.
Приведенная погрешность — погрешность показания, выраженная в долях или процентах номинального значения верхнего предела измерения прибора.
Приведенная погрешность ( или погрешность прибора) выражается в процентах.
Приведенная погрешность — погрешность показания, выраженная в долях или процентах номинального значения верхнего предела измерения прибора.
Приведенная погрешность при нормальных эксплуатационных условиях ( температура 20 С, правильная установка, отсутствие внешних магнитных полей и больших ферромагнитных масс) называется основной погрешностью прибора.
Приведенная погрешность и вариация должны быть меньше основной допустимой погрешности, которая определена классом точности прибора, обозначенным на шкале.
Приведенная погрешность — погрешность показания, выраженная в долях или процентах номинального значения верхнего предела измерения прибора.
Приведенная погрешность положена в основу определения класса точности приборов.
Как выбрать
Выбор лабораторных весов осложняется тем фактом, что на товарном рынке представлено огромное количество производителей и широкий модельный ряд. Более того, зачастую у одного производителя есть несколько моделей весов со схожими техническими характеристиками.
Все имеющиеся предложения необходимо соотнести с требованиями потенциального покупателя. Например, к классу точности, надёжности или наличию дополнительных функций. На основе этого можно выбрать наиболее оптимальную модель лабораторных весов.
Рассмотрим основные показатели, на которые необходимо обращать внимание при выборе весов
- НПВ, или наибольший предел взвешивания. Одна из основных характеристик в связи с тем, что разбег этого показателя огромен. Например, 1 г в микровесах, 20 г в аналитических весах или несколько кг в стандартных моделях.
- НиПВ, или наименьший вес, определяемый без погрешностей. Этот показатель также варьируется от мкг до г.
- Дискретность, или класс точности. Этот показатель уже рассматривался выше. В зависимости от целей использования прибора в будущем, необходимо определиться с подходящим классом. Советуем не покупать более высокий класс точности, чем вам необходимо. Во-первых, их цена значительно выше. Во-вторых, с повышенной точностью весы также становятся более чувствительными к внешним воздействиям. Таким устройствам нужны специальные условия для функционирования. Например, устойчивая поверхность или отсутствие воздушных потоков. Таким образом, приобретая более точный прибор, вы получаете лишь дополнительные сложности с обеспечением его работы. В то время как результат измерения будет такой же, как и на менее точных весах.
- Питание устройства. Прибор может работать от сети, батарейки либо их комбинации.
- Функция обнаружения массы тары. Наличие этой опции необходимо, чтобы избежать повышенной вероятности ошибки, когда масса навески практически равно минимальному пределу взвешивания.
Для некоторых покупателей необходимо наличие определённых функций в весах, помимо самой возможности взвешивания. Вот перечень дополнительных опций, которые предлагают производители:
- выбор единицы измерения;
- вывод на дисплее веса нетто;
- многокомпонентное (или иначе рецептурное) взвешивание;
- автоматическое отключение;
- системы пыле-, влаго-, взрывозащиты;
- функция выборки массы тары;
- возможность подключения к компьютеру или принтеру и т.д.
Также иногда приборы с аналогичными характеристиками имеют значительную разницу стоимости. Это связано с качеством сборки, стоимостью комплектующих и даже громким именем производителя. На стоимость влияет наличие гарантийного обслуживания. В данном случае необходимо определиться с теми характеристиками, которые для вас приоритетны.
Понятие и классификация
Под термином погрешность принято понимать степень отклонения реальной величины от вычисленной. Этот показатель служит мерой точности измерения.
Существует несколько разновидностей погрешности:

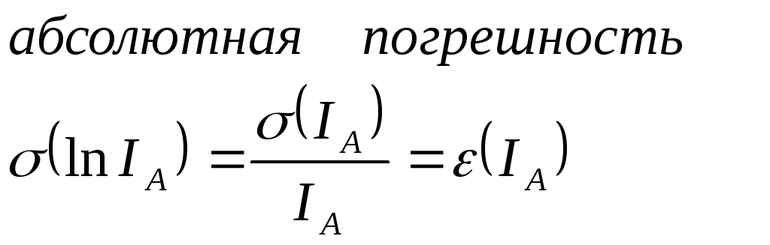
- Абсолютная — оценка ошибки в абсолютных единицах. Величина ее может быть разной в зависимости от способа расчета.
- Относительная — отношение абсолютной величины к тому значению, которое принято считать истинным. Измеряется в процентах.
- Приведенная — разновидность относительной. Ее вычисляют отношением абсолютной и условной постоянной величины, определяется в процентах.
- Приборная или инструментальная — погрешность, которую дают технические средства измерений. Она обусловлена неточной цифровой градуировкой приборов или недостаточной наглядностью. Класс точности приборов будет равен максимальной приведенной погрешности и выражается в процентах. К примеру, класс точности вольтметра ΔU = ±0,75 В.
- Методическая — связанная с несовершенством метода измерения или его чрезмерным упрощением.
- Субъективная или операторная — погрешность, связанная с личными свойствами оператора — невнимательностью, утомлением, профессиональной подготовленностью.
- Случайная. Погрешность, которая может изменяться при разных измерениях. Изменения возможны по знаку или величине отклонения. Причиной может быть техническое несовершенство приборов отсчета или объекта измерения, неблагоприятные для работы условия или особенности измеряемых единиц.
- Систематическая. Погрешность, изменения которой имеют некоторую закономерность во времени. В качестве частного случая допускают постоянное отклонение, которое не изменяется во времени.
- Прогрессирующая или дрейфовая — медленно изменяется во времени и не может быть предсказана. Такое отклонение относится к случайным.
- Грубая или промах. Значительное отклонение от принятой нормы. Возникает в результате неисправности аппаратуры или ошибки экспериментатора.









