Формула скорости — обозначение, единицы измерения и примеры нахождения

Скорость тела. Средняя скорость тела

      Решение задач на движение опирается на хорошо известную из курса физики формулу

позволяющую найти путь   S ,   пройденный за время   t   телом, движущимся с постоянной скоростью   v .

      Сразу же сделаем важное

      Замечание 1. Единицы измерения величин   S ,   t   и   v   должны быть согласованными. Например, если путь измеряется в километрах, а время – в часах, то скорость должна измеряться в км/час.

      В случае, когда тело движется с разными скоростями на разных участках пути, вводят понятие средней скорости, которая вычисляется по формуле

(1)

      Например, если тело в течение времени   t₁   двигалось со скоростью   v₁ ,  в течение времени   t₂   двигалось со скоростью   v₂ ,  в течение времени   t₃   двигалось со скоростью   v₃ ,  то средняя скорость

(2)

      Задача 1. По расписанию междугородный автобус должен проходить путь в   100   километров с одной и той же скоростью и без остановок. Однако, пройдя половину пути, автобус был вынужден остановиться на   25   минут. Для того, чтобы вовремя прибыть в конечный пункт, водитель автобуса во второй половине маршрута увеличил скорость на   20   км/час. Какова скорость автобуса по расписанию?

      Решение. Обозначим буквой   v   скорость автобуса по расписанию и будем считать, что скорость   v   измеряется в км/час. Изобразим данные, приведенные в условии задачи 1, на рисунке 1.

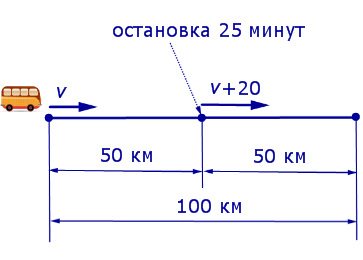
Рис. 1

      Тогда

      – время движения автобуса по расписанию (в часах);

      – время, за которое автобус проехал первую половину пути (в часах);

      v + 20   – скорость автобуса во второй половине пути (в км/час);

      – время, за которое автобус проехал вторую половину пути (в часах).

      В условии задачи дано время остановки автобуса –   25   минут. Его необходимо выразить в часах, чтобы все единицы измерения были согласованными:

      Теперь можно составить уравнение, исходя из того, что автобус прибыл в конечный пункт вовремя, а, значит, время, которое он был в пути, плюс время остановки должно равняться времени движения автобуса по расписанию:

      Решим это уравнение:

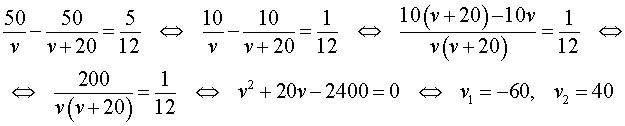
      По смыслу задачи первый корень должен быть отброшен.

      Ответ.   40   км/час.

      Задача 2. (МИОО) Первый час автомобиль ехал со скоростью   120   км/час, следующие три часа – со скоростью   105   км/час, а затем три часа – со скоростью   65   км/час. Найдите среднюю скорость автомобиля на протяжении всего пути.

      Решение. Воспользовавшись , получаем

      Ответ.   90   км/час.

      Задача 3. Первую половину пути поезд шел со скоростью   40   км/час, а вторую половину пути – со скоростью   60   км/час. Найдите среднюю скорость поезда на протяжении всего пути.

      Решение. Обозначим буквой   S   длину всего пути, выраженную в километрах. Изобразим данные, приведенные в условии задачи 3, на рисунке 2.

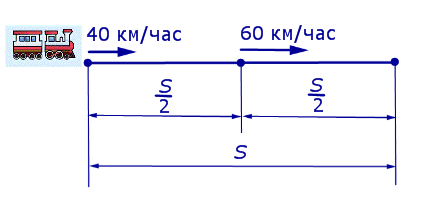
Рис. 2

      Тогда

      – время, за которое поезд прошел первую половину пути, выраженное в часах;

      – время, за которое поезд прошел вторую половину пути, выраженное в часах.

      Следовательно, время, за которое поезд прошел весь путь, равно

      В соответствии с средняя скорость поезда на протяжении всего пути

      Ответ.   48   км/час.

      Замечание 2. Средняя скорость поезда в задаче 3 равна   48   км/час, а не   50   км/час, как иногда ошибочно полагают, вычисляя чисел (скоростей)   40   км/час и   60   км/час. Средняя скорость не равна среднему арифметическому скоростей, а является величиной, вычисляемой по .

Средняя скорость — движение — автомобиль

Средняя скорость движения автомобиля зависит от максимальной скорости, которую он может развить на дорогах различного качества, и от интенсивности разгона. Кроме того, на среднюю скорость автомобиля существенное влияние оказывают его тормозные свойства.
 

Средние скорости движения автомобилей приведены для дорог с усовершенствованным типом покрытия в хорошем состоянии.
 

Средняя скорость движения автомобиля составляет v км / час.
 

Средняя скорость движения автомобиля зависит от многих факторов: на нее влияют, с одной стороны, конструктивные особенности автомобиля, а с другой — дорожные условия. При испытаниях ее стремятся поддерживать максимально возможной. Чтобы полнее выяснить причины, вызывающие ограничение скорости, принято определять среднюю скорость чистого движения и среднюю техническую скорость.
 

Стремление повысить среднюю скорость движения автомобилей ( автопоездов) при одновременном увеличении их полной массы приводит к повышению мощности двигателя, что, в свою очередь, вызывает повышенные требования к трансмиссии автомобиля. Это непосредственно относится и к ведущему мосту, назначение которого состоит в изменении крутящего момента двигателя при передаче его к ведущим колесам таким образом, чтобы вместе с коробкой передач обеспечить согласование скоростной характеристики двигателя с динамической характеристикой автомобиля.
 

График, для определения нагрузочного режима трансмиссии автомобиля ( по нормали.

Угловую скорость рассчитываемых подшипников определяют по средней скорости движения автомобиля аа ср — с учетом соответствующего передаточного числа между валами коробки передач.
 

Эффективность действия тормозов оказывает влияние на среднюю скорость движения автомобиля, особенно в условиях городского движения.
 

Именно эта скорость имеется в виду, когда, например, говорят о средней скорости движения автомобиля или средней скорости поезда.
 

За эквивалентное число оборотов пэкв принимается число оборотов подшипника ( вала), соответствующее средней скорости движения автомобиля на основной ( прямой) передаче.
 

Установка на шасси автомобиля двигателя повышенной мощности, ранее практиковавшаяся в Америке, повышала среднюю скорость движения автомобиля, уменьшала его износы и шумность работы, но ухудшала топливную экономичность. Последнее объясняется тем, что в двигателях большей мощности и большого рабочего объема при работе на малых нагрузках возрастает относительная величина тепловых, насосных и механических потерь.
 

Расстояние между площадками для кратковременных остановок и стоянок автомобилей зависит от интенсивности движения на дороге, средней скорости движения автомобилей, вместимости стоянки и средней продолжительности пребывания автомобиля на стоянке.
 

Зависимость коэффициента сцепления от различных факторов.

В практике управления автомобилем важно знать н только максимальную скорость движения автомобиля на отдельных участках маршрута, но и среднюю скорость на всем маршруте. Возможность определения средней скорости движения автомобиля имеет практическое значение для осуществления планирования перевозок грузов и пассажиров на автомобильном транспорте.
 . Из выражения ( 34) следует, что чем выше удельная мощность, тем больше ускорение разгона и меньше продолжительность этапа разгона до установившейся скорости

Из выражения ( 34) следует, что чем выше удельная мощность, тем больше ускорение разгона и меньше продолжительность этапа разгона до установившейся скорости

В итоге следует ожидать повышения средней скорости движения автомобиля. Для того чтобы оценить степень влияния удельной мощности на среднюю скорость вследствие сокращения именно этого этапа цикла, рассмотрим процесс разгона автомобиля с учетом переключения передач.
 

Из выражения ( 34) следует, что чем выше удельная мощность, тем больше ускорение разгона и меньше продолжительность этапа разгона до установившейся скорости. В итоге следует ожидать повышения средней скорости движения автомобиля. Для того чтобы оценить степень влияния удельной мощности на среднюю скорость вследствие сокращения именно этого этапа цикла, рассмотрим процесс разгона автомобиля с учетом переключения передач.
 

Какая средняя скорость и напишите формулу?

Средняя скорость рассчитывается по формуле S = d / t, где S — средняя скорость, d — общее расстояние, t — общее время. Проблемы: 1). Автомобиль проезжает расстояние 70 км за 2 часа.

то какая средняя скорость по математике? Средняя скорость объекта равна общее расстояние, пройденное объектом, деленное на время, затраченное на преодоление этого расстояния. Это скалярная величина, что означает, что она определяется только величиной.

Что является примером средней скорости? Средняя скорость рассчитывается путем деления общего пройденного расстояния на временной интервал. Например, тот, кто за 40 минут проехал 20 миль на север, а затем 20 миль на юг (чтобы оказаться в том же месте), имеет среднюю скорость 40 миль, разделенных на 40 минут, или 1 милю в минуту (60 миль в час).

Закон сложения

Для разных систем отсчёта движения материальных точек существует закон, связывающий их между собой. Согласно ему, скорость чего-либо относительно системы, находящейся в покое, определяется суммой силы перемещения скоростей в подвижной области и более быстрой системы отсчёта по отношению к неподвижной.

Чтобы понять суть закона, лучше всего рассмотреть простой пример. Пусть по железной дороге движется вагон со скоростью 80 км/ч. В этом вагоне перемещается пассажир со скоростью 3 км/ч. Приняв за систему отсчёта неподвижный железнодорожный путь, можно утверждать, что скорость пассажира относительно неё равна сумме скорости вагона и человека.

Если движение вагона и пассажира происходит в одном направлении, то значения просто складываются, V = 80+3 = 83 км/ч, в противоположном — вычитаются V = 80−3 = 77 км/ч. Но это правило будет верным лишь тогда, когда перемещение происходит по одной линии. Поэтому, если человек будет передвигаться в вагоне под углом, следует учитывать и этот фактор, так как по своей сути искомый параметр — величина векторная. Фактически рассчитываются две скорости: сближения и удаления.

Рассматриваемое событие происходит за время Δt. За этот промежуток человек преодолеет расстояние ΔS1, вагон же сможет проехать путь ΔS2. Используя закон, перемещение пассажира будет определяться по формуле: ΔS = ΔS1 + ΔS2. Собственное движение человека относительно железнодорожного пути будет равно V = ΔS1 / Δ t. Выразив значение из формулы нахождения ΔS, можно найти скорость вагона относительно железной дороги: V2 = ΔS2 / Δt.

Равномерное движение

Равномерное движение – это движение, при котором тело за любые равные промежутки времени совершает равные перемещения.

Скорость при равномерном движении – величина, равная отношению перемещения к промежутку времени, за которое это перемещение произошло:

Проекция вектора скорости на ось ОХ:

Проекция вектора скорости на координатную ось равна быстроте изменения данной координаты:

График скорости (проекции скорости)

График скорости (проекции скорости) представляет собой зависимость скорости от времени:

График скорости при равномерном движении – прямая, параллельная оси времени.
График 1 лежит над осью ​\( t \)​, тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью ​\( t \)​, тело движется против оси ОХ.

Перемещение при равномерном движении – это величина, равная произведению скорости на время:

Проекция вектора перемещения на ось ОХ:

График перемещения (проекции перемещения)

График перемещения (проекции перемещения) представляет собой зависимость перемещения от времени:

График перемещения при равномерном движении – прямая, выходящая из начала координат.
График 1 лежит над осью \( t \), тело движется по направлению оси ОХ.
Графики 2 и 3 лежат под осью \( t \), тело движется против оси ОХ.

По графику зависимости скорости от времени можно определить перемещение, пройденное телом за время \( t \). Для этого необходимо определить площадь фигуры под графиком (заштрихованной фигуры).

Координата тела при равномерном движении рассчитывается по формуле:

График координаты представляет собой зависимость координаты от времени: ​\( x=x(t) \)​.

График координаты при равномерном движении – прямая.
График 1 направлен вверх, тело движется по направлению оси ОХ:

График 2 параллелен оси ОХ, тело покоится.
График 3 направлен вниз, тело движется против оси ОХ:

Свободное падение (ускорение свободного падения)

Свободное падение – это движение тела в безвоздушном пространстве под действием только силы тяжести.

Все тела при свободном падении независимо от массы падают с одинаковым ускорением, называемым ускорением свободного падения.
Ускорение свободного падения всегда направлено к центру Земли (вертикально вниз).

Обозначение – ​\( g \)​, единицы измерения – м/с2.

Важно! \( g \) = 9,8 м/с2, но при решении задач считается, что \( g \) = 10 м/с2

Движение тела по вертикали

Тело падает вниз, вектор скорости направлен в одну сторону с вектором ускорения свободного падения:

Если тело падает вниз без начальной скорости, то ​\( v_0 \)​ = 0.
Время падения рассчитывается по формуле:

Тело брошено вверх:

Если брошенное вверх тело достигло максимальной высоты, то ​\( v \)​ = 0.
Время подъема рассчитывается по формуле:

Движение тела, брошенного горизонтально

Движение тела, брошенного горизонтально, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали со скоростью ​\( v_0=v_{0x} \)​;
2. равноускоренного движения по вертикали с ускорением свободного падения ​\( g \)​ и без начальной скорости ​\( v_{0y}=0 \)​.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Дальность полета:

Угол между вектором скорости и осью ОХ:

Движение тела, брошенного под углом к горизонту (баллистическое движение)

Движение тела, брошенного под углом к горизонту, можно представить как суперпозицию двух движений:

1. равномерного движения по горизонтали;
2. равноускоренного движения по вертикали с ускорением свободного падения.

Уравнение скорости:

Уравнение координаты:

Скорость тела в любой момент времени:

Угол между вектором скорости и осью ОХ:

Время подъема на максимальную высоту:

Максимальная высота подъема:

Время полета:

Максимальная дальность полета:

Важно!
При движении вверх вертикальная составляющая скорости будет уменьшаться, т. е

тело вдоль вертикальной оси движется равнозамедленно.
При движении вниз вертикальная составляющая скорости будет увеличиваться, т. е. тело вдоль вертикальной оси движется равноускоренно.
Скорость ​\( v_0 \)​, с которой тело брошено с Земли, будет равна скорости, с которой оно упадет на Землю. Угол ​\( \alpha \)​, под которым тело брошено, будет равен углу, под которым оно упадет.

При решении задач на движение тела, брошенного под углом к горизонту, важно помнить, что в точке максимального подъема проекция скорости на ось ОУ равна нулю:

Это облегчает решение задач:

Ускорение

Ускорение – это векторная физическая величина, характеризующая быстроту изменения скорости.

Обозначение — ​\( a \)​, единица измерения — м/с2.
В векторном виде:

где ​\( v \)​ – конечная скорость; ​\( v_0 \)​ – начальная скорость;
​\( t \)​ – промежуток времени, за который произошло изменение скорости.

В проекциях на ось ОХ:

где ​\( a_n \)​ – нормальное ускорение, ​\( a_{\tau} \)​ – тангенциальное ускорение.

Тангенциальное ускорение сонаправлено с вектором линейной скорости, а значит, направлено вдоль касательной к кривой:

Нормальное ускорение перпендикулярно направлению вектора линейной скорости, а значит, и касательной к кривой:

Ускорение характеризует быстроту изменения скорости, а скорость – векторная величина, которая имеет модуль (числовое значение) и направление.

Важно!
Тангенциальное ускорение характеризует быстроту изменения модуля скорости. Нормальное ускорение характеризует быстроту изменения направления скорости.
Если \( a_{\tau} \) ≠ 0, \( a_n \) = 0, то тело движется по прямой;
если \( a_{\tau} \) = 0, \( a_n \) = 0, ​\( v \)​ ≠ 0, то тело движется равномерно по прямой;
если \( a_{\tau} \) = 0, \( a_n \) ≠ 0, тело движется равномерно по кривой;
если \( a_{\tau} \) = 0, \( a_n \) = const, то тело движется равномерно по окружности;
если \( a_{\tau} \) ≠ 0, \( a_n \) ≠ 0, то тело движется неравномерно по окружности

Рекомендации

Если вы хотите заняться спортивной ходьбой в оздоровительных целях, то для этого вам понадобиться только удобные кроссовки и целеустремленный характер.

В завершение, несколько советов для новичков:

1. Любая хорошая привычка требует преодоления себя, самыми тяжелыми будут первые 3 недели, потом занятия станут необходимостью для вас.
2. Старайтесь получить удовольствие, а не просто пройти определенное количество километров – слушайте хорошую музыку, выбирайте интересные маршруты.
3. Выбирайте оптимальное время — в этом случае нет строгих рекомендаций, кому-то подходит утро, кому-то вечер.
4. Ставьте перед собой реально выполнимые цели. Например, пройти до определенного места за какое-то время.
5. Преодолевайте свою лень!

Когда среднее арифметическое «не подводит»

Если задача формулируется так: «За равные промежутки времени тело двигалось сначала со скоростью v₁, затем v₂, v₃ и так далее», быстрый ответ на вопрос, как найти среднюю скорость, может быть найден неправильным способом. Предоставим читателю самостоятельно в этом убедиться, просуммировав в знаменателе равные промежутки времени и воспользовавшись в числителе v_ср соотношением (1). Это, пожалуй, единственный случай, когда ошибочный метод приводит к получению корректного результата. Но для гарантированно точных расчётов нужно пользоваться единственно правильным алгоритмом, неизменно обращаясь к дроби v_ср = S : t.

Суть и определение

Суть неравномерного движения изучают в седьмом классе средней школы на уроках физики. В школьном учебнике приводится определение, что неравномерным считается такое изменение материальной точки в пространстве, при котором меняется скорость. При этом отмечается, что она может изменяться и по направлению.

Исходя из этого, можно сделать заключение, что движение, сопровождающее изменением скорости или траектории, является неравномерным. Например, вращение шара по окружности, выстрел из лука. При этом перемещение может быть равноускоренным, то есть состоять из чередования различных неравномерных движений. Как пример можно привести переключение скоростей в передвигающемся автомобиле.

Средняя скорость — это относительный параметр. Определяется он отношением пройденного пути к затраченному для этого времени. Предполагать, что для его нахождения можно просто сложить известные мгновенные скорости и разделить результат на их количество, в корне неверно. Под мгновенной характеристикой понимается скорость, существующая в определённой точке на данный момент.

Например, спидометр, установленный в машине, регистрирует ежесекундно именно мгновенную скорость. Поэтому для нахождения среднего показателя используется следующая формула: V = s / t, где:

В качестве единицы измерения используется отношение метров на секунды в соответствии с Международной системой измерений (СИ). Следует отметить, что когда траектория пути не является прямолинейной, то пройденное материальной точкой расстояние будет больше, чем её перемещение. Для описания такого случая вводится понятие средней путевой скорости, являющейся скалярной величиной. При этом её значение будет отличаться от средней скорости перемещения.

Случается так, что движение точки через один и тот же промежуток времени изменяется на одинаковую величину. В этом случае движение называют равнопеременным. Оно может быть как равнозамедленным, так и равноускоренным. Ускорение или замедление не зависит от изменения скорости за единицу времени. Но, зная поведение тела и его начальную скорость, можно вычислить, с какой скоростью оно будет двигаться в любой промежуток времени. Для этого используют выражение: v = v0 + a * Δt.

Какой должна быть средняя скорость машины в поездке?

Многие задаются вопросом, а какой же на самом деле должна быть средняя скорость автомобиля. Просчитав удивительный факт того, что средняя скорость авто в трассовом режиме составила всего 80 километров в час, водитель начинает сомневаться в том, что он эффективно использует ресурс транспортного средства. На самом деле, такая скорость вполне допустима.

Оптимальной скоростью при движении по трассе является 90 км/ч, но далеко не всегда получает держать крейсерскую скорость постоянно. Иногда происходят ситуации, которые заставляют в течение нескольких минут ехать медленно. К примеру, можно тянуться за фурой, ожидая возможности обгона. Оптимальная средняя скорость на трассе будет зависеть от таких факторов:

• дорожные условия и состояние дороги, по которой выполняется поездка в нужное вам место;
• количество транспорта, загруженность и сложность трассы для совершения обгонов медленных авто;
• наличие дополнительных полос для совершения маневров без снижения скорости машины;
• позволенная скорость и наличие средств автоматической фиксации нарушения ПДД или постов ГИБДД;
• соображения личной безопасности, которые исходят из состояния собственного автомобиля;
• тип транспорта, на котором вы преодолеваете дистанцию, его технические возможности и ограничения;
• погодные условия, наличие корки льда на трассе или мокрая дорога, снижающая хорошее сцепление.

Это лишь базовые факторы, которые влияют на среднюю скорость машины при трассовой поездке. На практике при отсутствии нарушений ПДД средняя скорость автомобиля на трассе составляет 75-80 километров в час. Достичь средней скорости в 90 км/ч можно только на определенном отрезке трассы. Потому не огорчайтесь, увидев небольшие значения на экране бортового компьютера.

Первым фактором, который нужно оценивать при выборе скоростного режима на трассе, является безопасность. Именно этот важный критерий иногда становится жертвой нехватки времени или желания показать достойные цифры средней скорости. На деле такие цели никогда не приводят к хорошим последствиям, потому всегда выбирайте безопасные режимы поездки.

Средняя скорость — машина

Средняя скорость машин ЕС-1030 по Гибсону составляет 100 тыс. операций в секунду.
 

Под средней скоростью машины понимают среднюю линейную скорость одной из точек ведущего вала машины во время ее установившегося движения.
 

Для того чтобы средняя скорость машины могла оставаться постоянной, необходимо, чтобы при этой скорости имело место равновесие между работой движущих сил и работой сопротивлений. Но это равновесие может нарушаться по различным причинам.
 

Для установления козфициента нагрузки двигателя определим среднюю скорость машины v — кгк, момент трения по формуле ( 55), угловую скорость машины ( см. фиг.
 

Очевидно, что такая система позволяет на уровне программирования заботиться о том, чтобы информация была заранее считана в быстрые регистры операндов и арифметическое устройство не ожидало ее поступления из памяти. Средняя скорость машины CDC-6600 оценивается в 3 5 млн. операций в секунду, однако, как утверждают разработчики, при оптимальном программировании она может быть значительно повышена.
 

Сравнение формул ( 52) и ( 58) дает следующий вывод: коэфициент нагрузки двигателя на повороте при бортовых фрикционах в два раза меньше, чем при простом дифе-ренциале. Это снижение нагрузки достигается за счет снижения потери в тормозе, а также вследствие понижения средней скорости машины на повороте. Зависимость между коэ-фициентами нагрузки двигателя и параметром поворота показана на диаграмме фиг.
 

Регуляторы являются приборами, предназначенными для того, чтобы удерживать в возможно близких друг к другу пределах изменения средней скорости машины, вызванные изменениями движущих сил или сил сопротивлений.
 

Если бы движение машины было равномерно, если бы она шла всегда одинаково быстро, то оценка 40 км в час полностью характеризовала бы ее скорость — одну и ту же в любой момент движения. Но машина движется неравномерно; за час скорость ее много раз резко меняется, и когда нам говорят, что машина прошла в час 40 км, то это дает нам представление лишь о некоторой средней скорости машины за этот час и ничего не говорит о скорости ее в тот или другой определенный момент, в том или другом определенном месте ее пути. Час — это слишком большой промежуток времени, за который скорость движения машины может меняться много раз.
 

Средняя скорость машины при выполнении арифметики тем самым приблизительно равна 10000 операций в секунду. При выполнении логических программ быстродействие резко возрастает. В минимальном комплекте в состав процессора входит оперативная память объемом 8192 байта. Правда, объем памяти при необходимости может быть расширен до 64 Кбайт.
 

На маршруте ABCDE длиной 147 км Турист может сам выбирать способ передвижения. На обратном пути из пункта Е в пункт А он поступил по-другому: до пункта D дошел пешком, преодолев расстояние в 24 км, в пункте D пересел на лошадь и добрался до пункта В за 3 ч 20 мин, а от пункта Л до пункта А доехал на машине за 1 ч 12 мин. Определите скорость передвижения туриста на машине и на лошади, если средние скорости машины и лошади были постоянными при движении от А к S и обратно.